Вероятностно-стоимостные модели функционирования ЛА

Согласно схеме ЭО, рассмотренной выше, вначале проводятся автономные испытания в процессе которых оценивается работоспособность отдельных элементов систем. При планировании автономных испытаний в результате решения задачи нормирования надежности оцениваются рациональные объемы испытаний отдельных элементов систем и потребные уровни их резервирования . Решение этой задачи рассмотрено в разделе .

Затраты на обеспечение надежности отдельных систем на этапе их автономных испытаний будут зависеть от уровней избыточности элементов, входящих в состав анализируемых систем

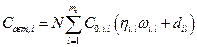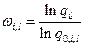где - кратность резервирования l – го элемента I – ой системы;

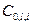- стоимость нерезервированного l -го элемента I – ой системы;

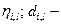коэффициенты аппроксимации;

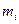– число элементов в составе I – ой системы.

Учитывая соотношение ( 3.5 ), выражение для 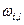можно представить в ви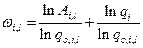де

, где .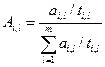

После подстановки в соотношение для стоимости, получим

,

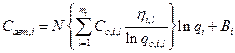где .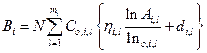

При одинаковых значениях коэффициентов 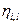и вероятностей 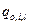соотношение упростится

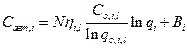, где .

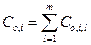Знание надежности отдельных элементов позволяет рассчитать надежность системы в целом. Однако полученная оценка надежности требует уточнения, так как она не учитывает возможность появления новых источников отказа, возникающих при совместном функционировании элементов в составе системы. Выявить эти источники отказа возможно только на этапе стендовых комплексных испытаний систем. При проведении комплексных испытаний реальная надежность системы повышается за счет устранения выявленных источников отказа. При этом изменение вероятности отказа, обусловленной взаимодействием элементов, входящих в состав системы, по числу испытаний для произвольного j – го этапа комплексной отработки, можно представить в виде [ 3 ]

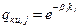, ( 2.48 )

где 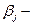эффективность проведения ЭО;

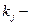число испытаний.

После отработки отдельных систем ЛА проводят комплексные испытания систем, работающих совместно. Эти испытания проводятся поэтапно. Например, вначале проводятся огневые наземные испытания всего РБ, а потом следуют летные испытания РБ в составе штатного носителя.

Очевидно затраты на обеспечение надежности при проведении j – го этапа комплексной отработки будут определяться стоимостью проведения испытаний и затратами на устранение обнаруженных неисправностей.

В линейном приближении можно принять

;

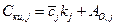где 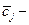удельные затраты на одно испытание;

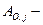прочие затраты с учетом проведения доработок при отказах.

Учитывая зависимость ( 2.48 ) имеем

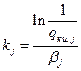
Отсюда

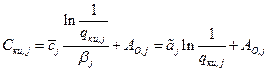, ( 2.49 )

где .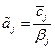

Заметим, что коэффициент 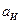характеризует затраты, приходящиеся на обеспечение единицы надежности в процессе проведения ЭО.

В предположении, что по каждому параметру подтверждаются одинаковые уровни надежности, значение 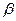можно оценить по соотношению

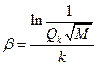, ( 2.50 )

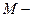число исследуемых источников отказа;

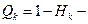уровень вероятности отказа.

Согласно [ 7 ] величина 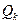рассчитывается по соотношению

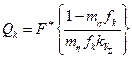, ( 2.51 )

где .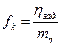

Зависимости параметра 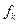от числа испытаний для разных M, полученные в работе [ 7 ], представлены на рис. 2.12—2.15 . Знание 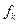позволяет оценивать искомые значения 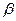по соотношениям ( 2.50 ), ( 2.51 ) для любых заданных уровней параметрической избыточности .

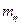Характер изменения параметра 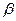в зависимости от k при различном числе источников отказа M, коэффициентах вариаци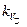и и 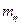представлен на рис.2.16—2.19. . На этих же графиках нанесены кривые, характеризующие рост подтверждаемой надежности с увеличением числа испытаний.

Анализ полученных результатов показывает, что эффективность отработки падает с увеличением числа испытаний. Как и следовало ожидать, величина 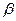убывает с увеличением числа источников отказа M и относительного разброса параметров 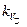и растет с увеличением уровня избыточности .

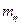Представленные выше результаты позволяют производить оперативный прогноз эффективности отработки 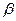при разработке программ экспериментальной отработки перспективных ЛА.

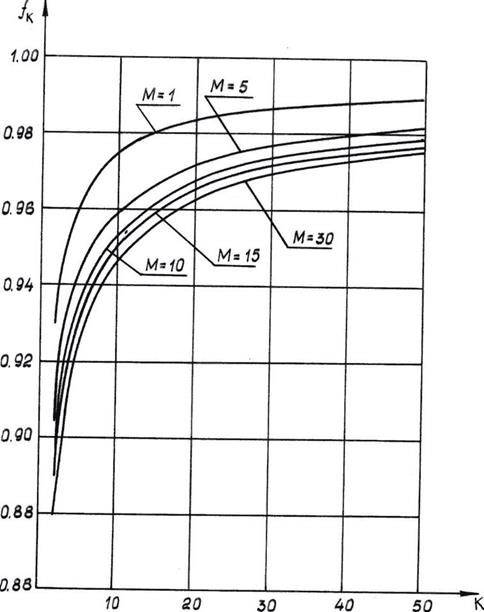
Рис. 2.12 Изменение параметра 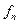по числу испытаний ( = 0,05 ).

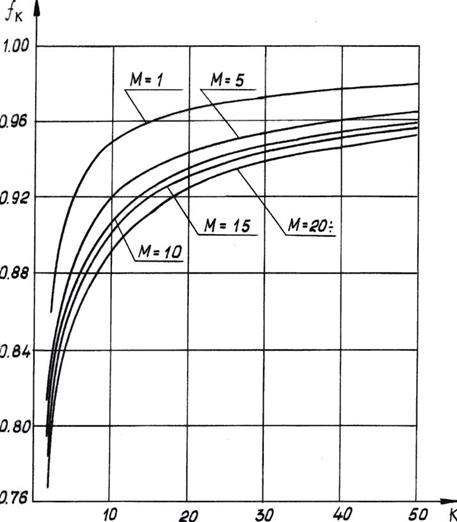
Рис.2.13 Изменение параметра 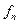по числу испытаний ( =0.1 ).

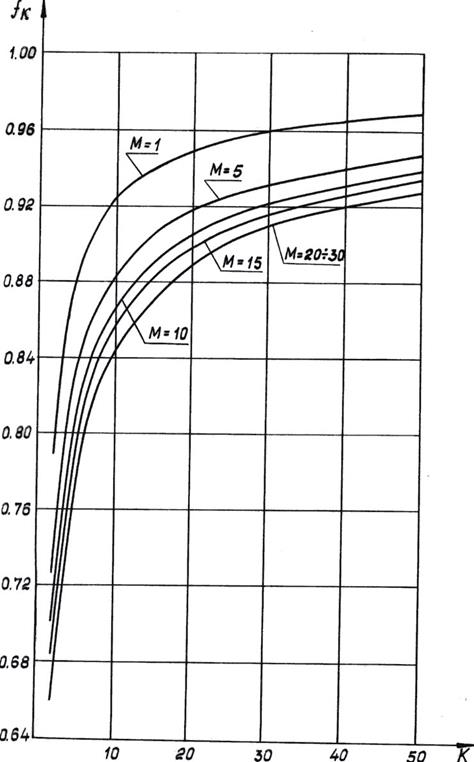
Рис.2.14 Изменение параметра 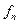по числу испытаний ( 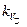= 0.15 ).

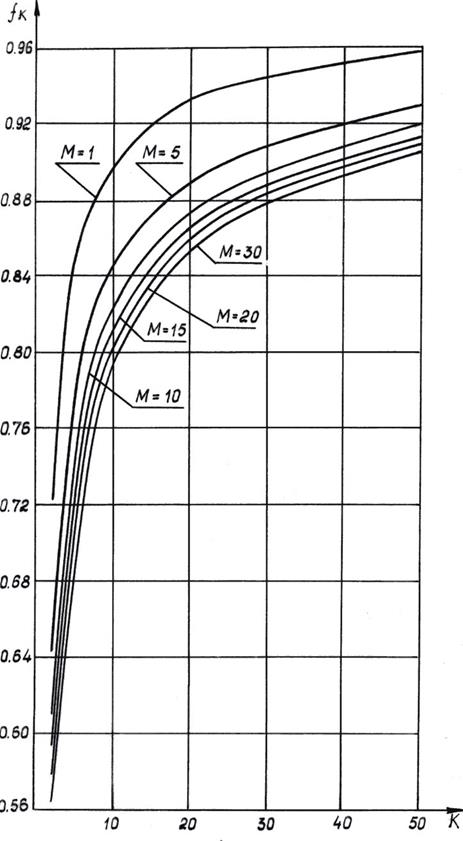
Рис. 2.15 Изменение параметра 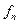по числу испытаний ( 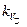=0.2 ).

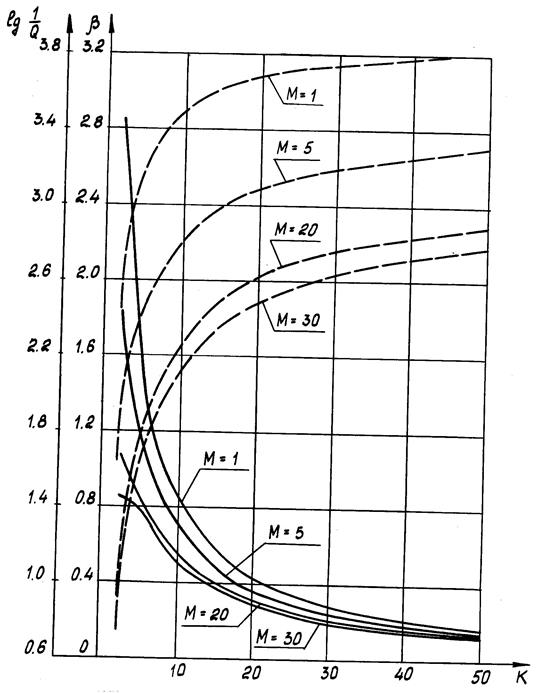
Рис. 2.16 Изменение показателя эффективности опытной отработки

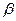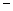( ) и подтверждаемых уровней надежности ( --)

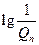по числу испытаний ( ).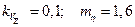

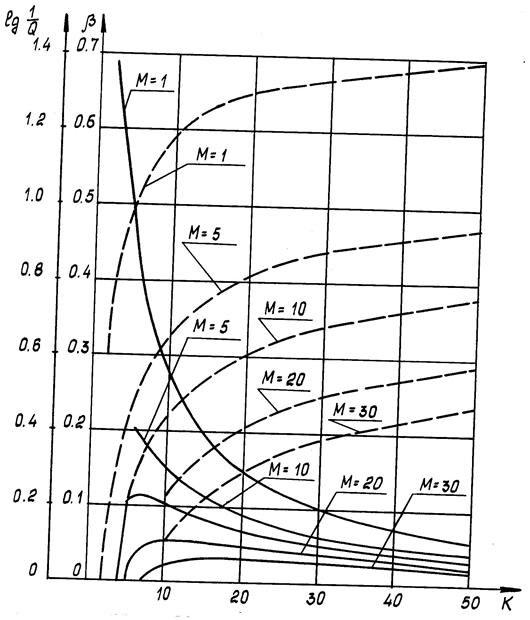
Рис. 2.17 Изменение показателя эффективности опытной отработки

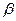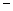( ) и подтверждаемых уровней надежности ( --)

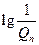по числу испытаний ( ).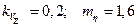

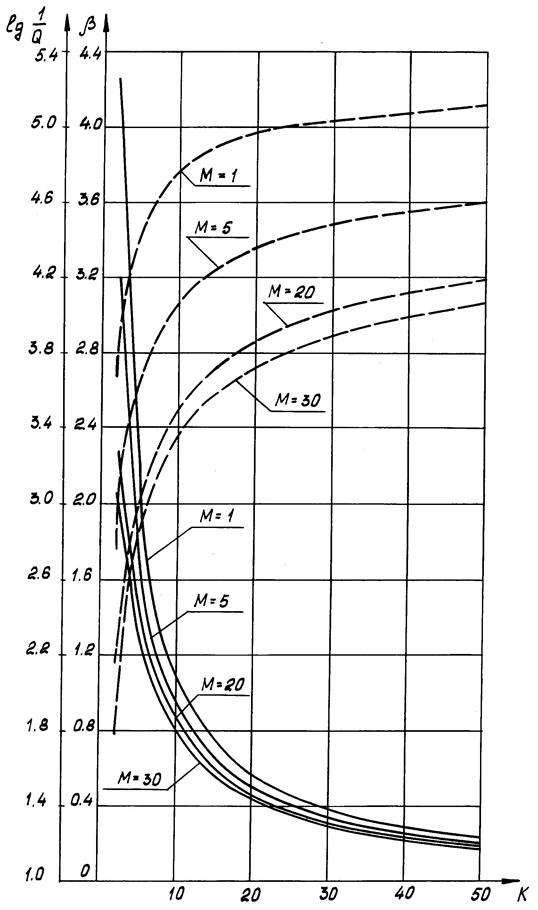
Рис. 2.18 Изменение показателя эффективности опытной отработки

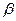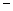( ) и подтверждаемых уровней надежности ( --)

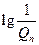по числу испытаний ( ).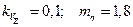

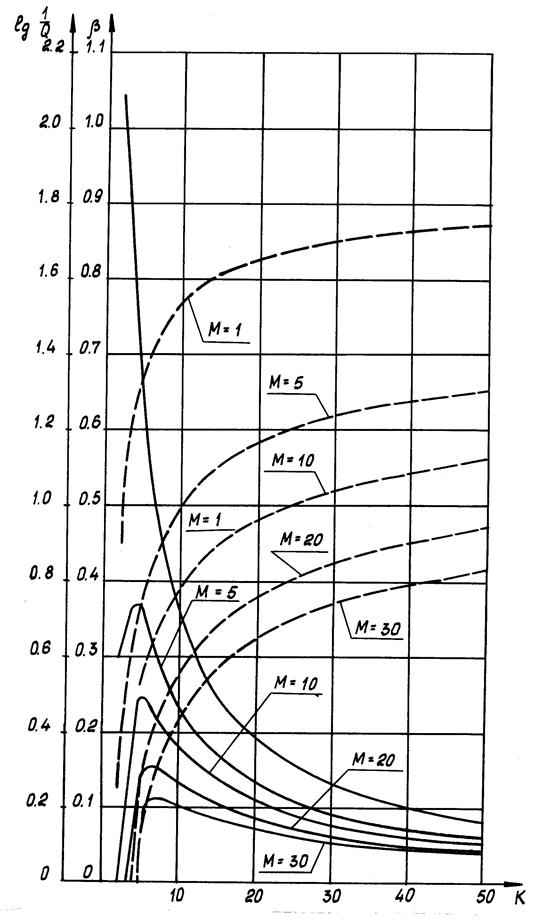Рис. 2.19 Изменение показателя эффективности опытной отработки

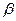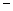( ) и подтверждаемых уровней надежности ( --)

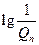по числу испытаний ( ).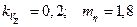

Планирование ЭО ЛА.

Планирование ЭО заключается в определении объема испытаний на каждом из этапов экспериментальной отработки ЛА и его систем. В результате проведения полного цикла испытаний должны быть удовлетворены требования, предъявляемые к надежности аппарата, то-есть

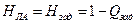, ( 2.52 )

где ; ; ;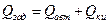

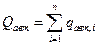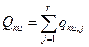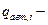вероятность отказа, достигаемая на этапе автономной отработки j-ой системы;

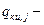вероятность отказа, достигаемая на j-ом этапе комплексной отработки ЛА;

n - число систем в составе ЛА;

r - число этапов комплексных испытаний.

Как видно из соотношения ( 2.52 ) заданные уровни надежности ЛА можно обеспечить при различных сочетаниях вероятностей отказа 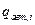и .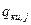

При этом конкретные уровни вероятности отказа, соответствующие автономным испытаниям 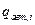и комплексных испытаний 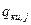, удовлетворяющие дисциплинирующему условию ( 2.52 ), целесообразно назначать из условия минимизации суммарных затрат 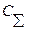на проведение ЭО.

.

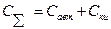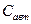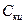Согласно результатам, полученным выше, выражения для и можно представить в виде

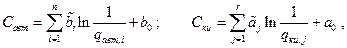
где ; ; ;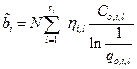

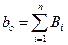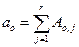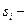число элементов в составе i-ой системы.

Таким образом выражение для 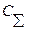,без свободных членов, примет вид

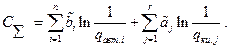
Для рассматриваемого случая функция Лагранжа будет равна

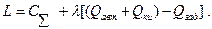
Таким образом оптимальные уровни вероятностей отказа 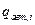и 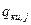должны удовлетворять соотношениям

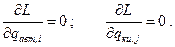
Раскрывая выражения для производных, приходим к системе алгебраических уравнений

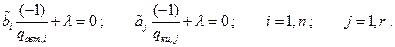
Разрешая уравнения относительно вероятностей отказа, получим

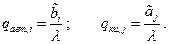
После подстановки в дисциплинирующее условие будем иметь

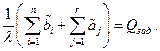
Отсюда

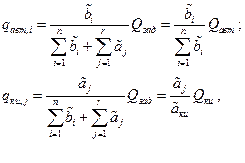( 2.53 )

где .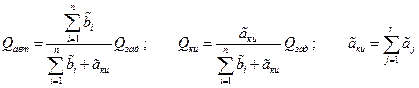

Знание 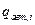позволяет оценить вероятности отказа отдельных элементов систем и объемы их испытаний .

В частности, для нормального закона распределения параметров работоспособности, получим

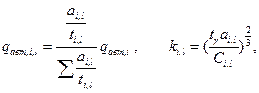
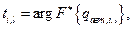
где 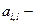коэффициент чувствительности l-го элемента i-ой системы ;

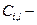стоимость проведения одного испытания l-го элемента i-ой системы;

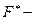функция нормированного нормального распределения .

При этом потребные уровни избыточности элементов систем оцениваются по соотношениям

,

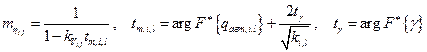где 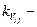коэффициент вариации l-го элемента i-ой системы

На этапах комплексной отработки объемы испытаний оцениваются по соотношению

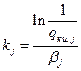. ( 2.54 )

Таким образом, предложенный подход позволяет разрабатывать программу экспериментальной отработки изделия, обеспечивающую удовлетворение требований, предъявляемых к надежности ЛА при минимальных затратах материальных средств.

Пример. Для иллюстрации предлагаемого подхода рассмотрим модельный пример разработки программы ЭО космического разгонного блока (КРБ ).

Надежность КРБ определяется безотказной работой всех систем, входящих в его состав. Основные системы КРБ и их характеристики, принятые в расчете, представлены в табл. 2.1.

Характеристики систем КРБ Таблица 2.1

№	Система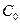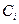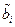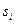
	Конструкция	0,42	0,84	2,25
	Маршевый двигатель	0,34	0,34	1,83
	ПГС	0,08	0,02	0,43
	ДУ СООЗ	0,04	0,04	0,22
	Средства разделения	0,02	-	-
	СТР	0,08	0,02	0,43
	Прочие системы	0,02	0,01	0,11

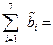5,3

При формировании конкретных исходных данных, представленных в таблице, первоначально оценивались массово-энергетические и стоимостные характеристики систем КРБ, полученные на этапе проведения проектных расчетов. В таблице представлены безразмерные стоимости, отнесенные к общей стоимости аппарата без учета затрат на топливо и стоимости полезной нагрузки.

При оценке удельной стоимости проведения одного испытания , помимо стоимости самой системы , учитывались дополнительные затраты на топливо, электроэнергию и необходимые расходные материалы, а также затраты на амортизацию оборудования и оплату труда персонала. Очевидно все это приводит к тому, что затраты на проведение одного испытания будут превышать стоимость самой системы . Однако , с другой стороны, необходимо учитывать, что наличие однотипных элементов в составе системы приводит к уменьшению стоимости проведения испытаний по сравнению со стоимостью самой системы. Число элементов 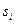, входящих в состав каждой системы, представлено в последнем столбце таблицы. Очевидно эти элементы могут различаться по надежности. Однако в дальнейшем, для упрощения расчетов, все элементы в составе отдельной системы будем считать равнонадежными. В этом случае коэффициенты чувствительности 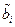оценивались по соотношению

.

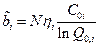При проведении расчетов объем программы полетов был принят равным 100.

Кроме того предполагалось параметрическое резервирование систем. Поэтому для всех элементов систем было принято значение 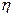равное 0.25.

Наконец для всех элементов систем принят одинаковый уровень начальной надежности, соответствующей вероятности отказа 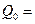0.01.

После отработки отдельных элементов систем переходят к комплексным испытаниям. На этапе комплексной отработки рассматривались комплексные испытания систем, огневые испытания ступени и летные испытания изделия.

При анализе комплексных испытаний требуется оценить параметр .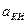

Согласно (4.2) величина этого параметра рассчитывалась по соотношению

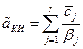
где 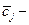удельная стоимость одного испытания на j-ом этапе комплексной отработки, 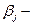эффективность отработки, соответствующая j-ому комплексных испытаний.

На этапе комплексной отработке систем стоимость проведения одного испытания принималась больше стоимости системы, в виду существенного увеличения затрат на стендовое оборудование и их обслуживание. На этапе огневых испытаний КРБ и летных испытаний стоимость проведения одного испытания принималась равной утроенной стоимости объекта испытаний.

Результаты расчета параметров комплексной отработки представлены в табл.2.2.Помимо удельных стоимостей в этой же таблице приведены значения эффективности проведения экспериментальной отработки .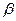

Значения 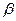оценивались в зависимости от предполагаемых характеристик

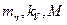, значения которых определяются типом системы и этапом экспериментальной отработки( см. рис. 2.16—2.19 ).

При проведении расчетов для заданного уровня надежности РБ в целом, принятого равным 0.988, оценивались оптимальные уровни надежности отдельных систем РБ, а также оптимальные объемы испытаний, обеспечивающие подтверждение требуемого уровня надежности при минимальных затратах средств.

Параметры комплексной экспериментальной отработки КРБ. Таблица 2.2

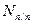	Этапы испытаний	Оценка	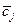Оценка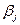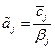
	Конструкция	-	-	-
	Маршевый двигатель	0.68	0,68
	ПГС	0.16		0.16
	ДУ СООЗ	0.08	1,5	0.05
	Средства разделения	0.08		0.04
	СТР	0.16		0.16
	Прочие системы	0,04	1,2	0.03
	Огневые испытания ступени			1,5
	Летные испытания

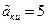
При решении вопросов нормирования надежность унифицированных элементов системы разделения предполагалась известной .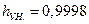

С учетом исключения унифицированных элементов надежность разгонного блока, подтверждаемая в процессе экспериментальной отработки, будет равна

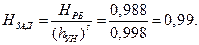
Распределение этой надежности между этапами экспериментальной отработки оценивалось по соотношениям

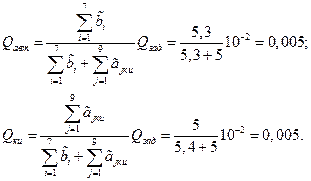
Вероятности отказа отдельных систем, подтверждаемые при их автономных и комплексных испытаниях оценивались по соотношениям

.

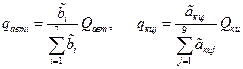Для отдельных элементов систем, в предположении их равнонадежности, получим

.

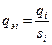В этом случае объемы испытаний элементов систем на этапе автономной отработки приближенно можно оценить по соотношению

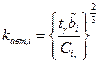
Соответственно количество испытаний при комплексной отработке систем рассчитывалось по соотношению

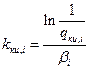, ( i= 1--7 )

где 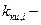число испытаний на этапе комплексной отработки i-ой системы.

Результаты расчета представлены в табл. 2.3.

Результаты расчета характеристик надежности и объема испытаний бортовых систем Таблица 2.3

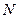	Системы КРБ	Надежность систем, подтверждаемая на этапе автономных испытаний	Надежность элементов систем, подтверждаемая при автономных испытаниях	Количество автономных испытаний элементов систем	Надежность систем, подтверждаемая при комплексных испытаниях	Количество испытаний при комплексной отработке систем
	Конструкция	0.9978	0.99955		-	-
	Маршевый двигатель	0.9982	0.99982		0.996
	ПГС	0.9996	0.99998		0.9996
	ДУ СООЗ	0.9998	0.99998		0.9998
	Средства разделения	0.9980	0.99980	-	0.9999
	СТР	0.9994	0.99998		0.9996
	Прочие системы	0.9997	0.99999		0.9999

Соответственно количество испытаний на отдельных этапах комплексных испытаний будет равно

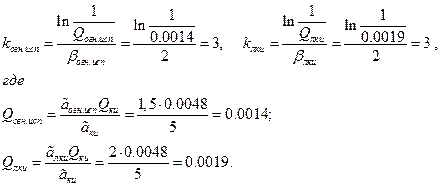
После проведения расчетов оценивается возможность достижения полученных характеристик систем и проводится корректировка результатов расчета.