Поняття про імпульсні системи автоматичного керування
ІМПУЛЬСНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ
У зв’язку з бурхливим розвитком обчислювальної техніки у промисловій автоматиці все більшого застосування набувають системи, робота яких пов’язана з впливом, передачею і перетворенням послідовності імпульсів, тобто дискретні системи. До складу дискретної системи разом із ланками безперервної дії входять елементи, які перетворюють безперервні сигнали у дискретні, і елементи, що виконують зворотне перетворення.
Процес перетворення безперервного сигналу на імпульсну послідовність виконується двома етапами:
- квантування сигналу, тобто перетворення безперервного сигналу на дискретний;
- перетворення квантованого сигналу відповідно до одного із законів модулювання на імпульсну послідовність, що діє на об’єкт.
Розрізняють три види квантування сигналів: за рівнем, за часом, за рівнем і за часом одночасно.
Квантування за рівнем полягає у фіксації визначених дискретних значень безперервного сигналу. При цьому безперервний сигнал замінюється сигналом, який змінюється східчасто. Суміжні дискретні значення відрізняються один від одного на постійну величину 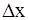 , яка називається кроком квантування. Перехід з одного рівня на інший відбувається у моменти часу, коли безперервний сигнал досягає чергового фіксованого значення (рис. 8.1, а), або коли сигнал проходить середину інтервалу між двома суміжними значеннями (рис. 8.1, б).
, яка називається кроком квантування. Перехід з одного рівня на інший відбувається у моменти часу, коли безперервний сигнал досягає чергового фіксованого значення (рис. 8.1, а), або коли сигнал проходить середину інтервалу між двома суміжними значеннями (рис. 8.1, б).
Квантування за часом полягає у фіксації значень безперервного сигналу в рівновіддалені один від одного дискретні моменти часу. При цьому квантований сигнал може мати східчасту форму (рис. 8.1, в) або являти собою послідовність імпульсів (рис. 8.1, г). Суміжні моменти відрізняються один від одного на постійну величину Dt = T, яка називається інтервалом дискретності або періодом повтору.
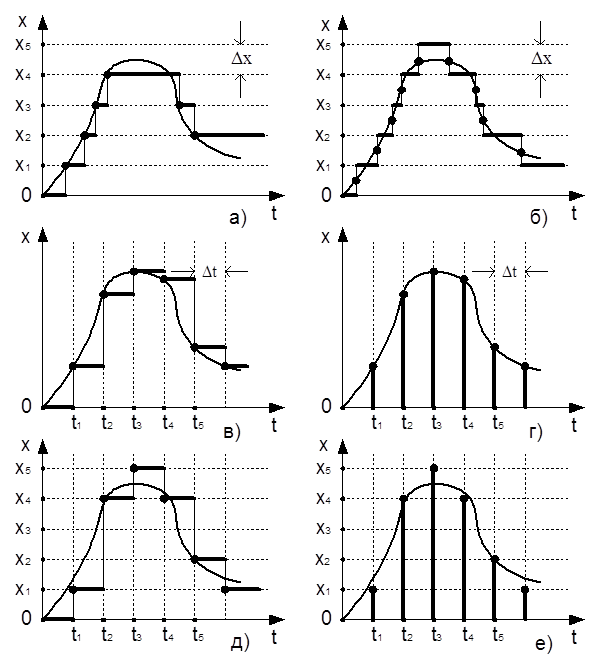
Рис. 8.1 - Види квантування сигналів: за рівнем (а; б), за часом (в; г),
за рівнем і за часом (д; е)
Під час сумісного квантування за рівнем і за часом фіксуються дискретні за рівнем значення, найближчі до значень безперервного сигналу в дискретні моменти часу (рис. 8.1, д, е).
Залежно від виду квантування, що застосовується, всі дискретні системи можна розділити на три класи:
- релейні; у них квантування відбувається за рівнем;
- імпульсні, в яких квантування відбувається за часом;
- цифрові (релейно-імпульсні) з квантуванням і за рівнем, і за часом.
Квантування за рівнем у релейних системах відбувається за допомогою спеціальних елементів – квантувачів. Найпростішим квантувачем є дво- та трипозиційні реле. Вони квантують безперервний сигнал відповідно за двома і трьома рівнями.
Квантування за часом відбувається за допомогою імпульсного елемента.
Одночасне квантування сигналів за рівнем і за часом у цифрових системах виконується за допомогою аналого-цифрових перетворювачів (АЦП).
На другому етапі перетворення квантований сигнал відповідно до одного із законів модуляції перетворюється на імпульсну послідовність. У САК найчастіше використовують такі види модуляції:
- амплітудно-імпульсна (АІМ);
- імпульсна (ІМ);
- імпульсно-кодова (ІКМ);
- широтно-імпульсна (ШІМ);
- частотно-імпульсна (ЧІМ).
Широке застосування систем керування з різними видами модуляції сигналу пояснюється низкою їх переваг:
- можливість багатоканального керування, тобто дискретний керуючий пристрій можна використовувати для одночасного керування декількома однотипними об’єктами;
- можливість стикування з цифровими обчислювальними пристроями, що дозволяє реалізувати більш складні закони керування;
- можливість тривалого збереження і запам’ятовування інформації;
- висока перешкодозахищеність, надійність; підвищена точність передавання і перетворення сигналів;
- менші габарити та вага; зручність для агрегатного-блочної побудови систем.
САК з імпульсною модуляцією сигналу відрізняється від безперервної системи наявністю імпульсного модулятора, який перетворює безперервний вхідний сигнал на послідовність імпульсів. Залежно від того, який з параметрів імпульсної послідовності модулюється, тобто змінюється під дією модулюючого сигналу, розрізняють:
- амплітудно-імпульсний модулятор, якщо модулюється амплітуда вихідних імпульсів; при цьому тривалість імпульсів t= const і період слідування 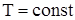 ;
;
- широтно-імпульсний модулятор, якщо модулюється ширина (тривалість) t вихідних імпульсів; при цьому амплітуда 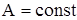 ;
; 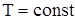 ;
;
- частотно-імпульсний модулятор, якщо модулюється частота повтору імпульсів у вихідній імпульсній послідовності; амплітуда і тривалість імпульсів постійні, тобто 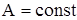 ; t = const.
; t = const.
Будемо вважати у подальшому, що за будь-якого типу модулятора полярність вихідних імпульсів буде змінюватись під час зміни полярності модулюючого сигналу. Такі модулятори називають двотактними (двополярними).
Види модуляції розділяють на модуляцію 1-го і 2-го роду. Модуляція першого роду характеризується тим, що параметри імпульсів, які модулюються, визначаються тільки значеннями модулюючого сигналу у фіксовані дискретні моменти часу і не залежать від зміни сигналу між ними. При модуляції другого роду значення параметра, що модулюється, визначається модулюючим сигналом, визначеним на кінцевому інтервалі часу, наприклад, протягом часу дії імпульсу.
Імпульсні системи бувають лінійними і нелінійними. Імпульсна система є лінійною, якщо безперервна частина системи та імпульсний елемент описуються лінійними рівняннями. Зазначимо, що імпульсний елемент, який здійснює амплітудно-імпульсну модуляцію, звичайно описується лінійними різницевими рівняннями, тому системи з АІМ можуть бути лінійними. Системи з ШІМ та ЧІМ є принципово нелінійними.
Основну увагу в даному розділі буде приділено лінійним системам із АІМ.
8.2 Функціональна й алгоритмічна структури системи з амплітудно-імпульсною модуляцією
Розглянемо структуру найпоширенішої імпульсної системи – системи з амплітудною модуляцією першого роду.
У загальному випадку імпульсний елемент системи може входити до складу будь-якого з її функціональних блоків, але найчастіше імпульсний характер системи зумовлений особливостями функціонування її сприймаючого або порівнювального блока. Наприклад, у системах керування технологічними процесами часто використовують датчики дискретної дії.
Типова функціональна схема імпульсної САК зображена на рис. 8.2, а. Для полегшення аналізу імпульсної САК реальний імпульсний елемент (ІЕ) замінимо еквівалентним послідовним з’єднанням найпростішого імпульсного елемента (НІЕ) і формувача імпульсів (ФІ) (рис. 8.2, б).
 |
НІЕ перетворює безперервний сигнал на послідовність миттєвих рівновіддалених один від одного імпульсів, яку можна подати у вигляді послідовності 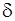 -функцій, промодульованих дискретними значеннями вхідного сигналу
-функцій, промодульованих дискретними значеннями вхідного сигналу 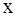 (рис. 8.3). Формувач імпульсів перетворює ці
(рис. 8.3). Формувач імпульсів перетворює ці 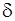 -імпульси на імпульси заданої форми (у розповсюдженому випадку – прямокутної форми тривалості t).
-імпульси на імпульси заданої форми (у розповсюдженому випадку – прямокутної форми тривалості t).
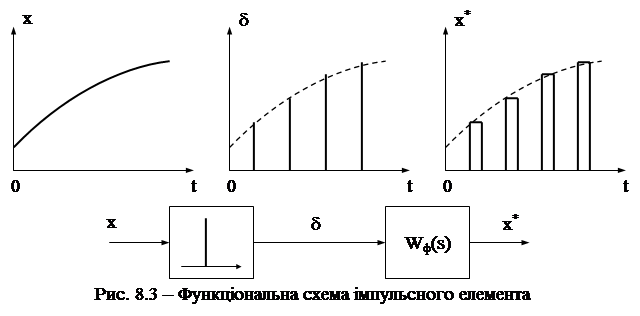 |
Оскільки реакція ланки на d- імпульси становить імпульсну перехідну або вагову функцію w(t), то передавальна функція формувача імпульсів у цьому випадку:
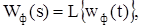 (8.1)
(8.1)
де wф(t) – імпульсна перехідна функція формувача імпульсів.
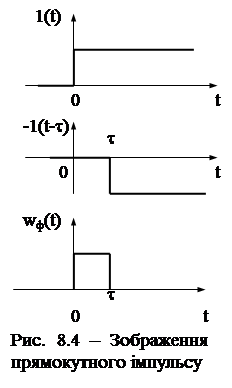 Прямокутний імпульс на виході формувача можна зобразити як суму додатної та від’ємної ступінчастих функцій, що зсунуті на час t = gТ0 (рис. 8.4), тобто
Прямокутний імпульс на виході формувача можна зобразити як суму додатної та від’ємної ступінчастих функцій, що зсунуті на час t = gТ0 (рис. 8.4), тобто
wф(t) = 1(t) – 1(t-t). (8.2)
Тоді
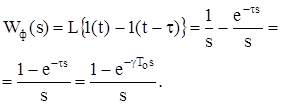 (8.3)
(8.3)
Т0 – період слідування імпульсів;
g = t/Т0 – відносна тривалість імпульсів.
За умови g=1 (сигнал на виході імпульсного елемента зберігається протягом усього періоду Т0 слідування імпульсів) передавальна функція формувача має вигляд:
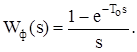 (8.4)
(8.4)
Такий імпульсний елемент називається екстраполятором нульового порядку або екстраполятором із фіксацією на період. При низьких частотах, коли частота вхідної дії wвх << 1/Т0, цей елемент за своїми властивостями є близьким до ланки запізнення з часом запізнення t=Т0/2, тобто
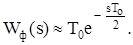 (8.5)
(8.5)
При високих частотах елемент (8.4) є еквівалентним ідеальній інтегруючій ланці й послаблює вхідний сигнал.
Якщо тривалість імпульсу значно менша за період, тобто g << 1, можна записати:
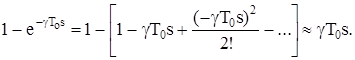 (8.6)
(8.6)
Тоді передавальна функція формувача імпульсів має вигляд:
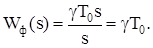 (8.7)
(8.7)
Для прямокутного імпульсу з амплітудою К відповідно до (8.4, 8.7) можна записати:
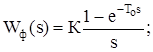
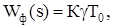 (g << 1). (8.8)
(g << 1). (8.8)
Аналогічно передавальні функції формувача імпульсів можна отримати для інших форм імпульсів на його виході.
Зі збільшенням частоти слідування імпульсів властивості розімкнутої амплітудно-імпульсної системи наближаються до властивостей її приведеної безперервної частини. Я.З. Ципкін зазначив, що умовою еквівалентності імпульсної системи та її приведеної частини є дві нерівності:
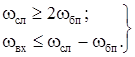 , (8.9)
, (8.9)
де wсл = 2p/Т0 – частота слідування імпульсів; wбп – частота, яка визначає смугу пропускання безперервної частини; wвх – найбільша частота спектра зовнішньої дії на вході імпульсного елемента.
Умови (8.9) тісно пов’язані з відомою у теорії інформації теоремою Котельникова-Шеннона: безперервний сигнал, спектр якого обмежений частотою wвх , можна без втрати інформації замінити на послідовність його дискретних значень, частота слідування яких wсл не менша за подвоєну верхню частоту wвх.
За умови виконання нерівностей (8.9) імпульсний елемент можна не враховувати і досліджувати систему як безперервну. Якщо ці умови не виконуються, то необхідно враховувати специфічні особливості імпульсної системи і застосовувати спеціальні засоби математичного опису.
