Координаттарымен берілген векторларға амалдар қолдану

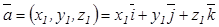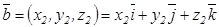, болса,

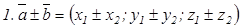
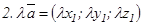
Векторлардың теңдігі

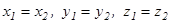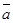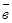болғанда ғана және векторлары тең болады, яғни

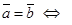
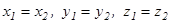
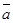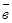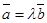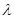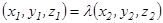
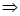
Векторлардың коллинеарлығы. || болғандықтан оны деп жазуға болады, мұндағы - қайсыбір сан. Осыдан 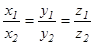-екі вектордың коллинеарлығының белгісі.

Нүктенің координатасы.Кеңістікте тік бұрышты декарттық 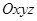координаттар жүйесі берілсін. Кез келген М нүктесінің координаты деп, 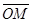векторының координатын айтады. 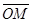векторы М нүктесінің радиус-векторы деп аталады және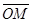 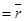деп белгіленеді. Сонымен, 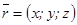немесе 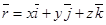. М нүктесінің координатасы 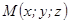деп жазылады.

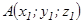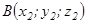Вектордың координатасы.Егер және нүктелерінің координаттары берілсе, онда 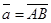векторының координатасы былай есептелінеді: .

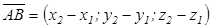3-мысал. 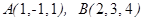берілсе, онда базисінде .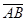

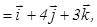
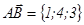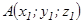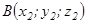Кесіндіні берілген қатынаста бөлу. және нүктелері арқылы өтетін кесінді берілсін. Осы кесіндіні 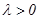қатынасындай етіп бөлетін 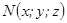нүктесінің координаттары: 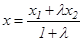, , 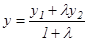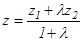- кесіндіні берілген қатынаста бөлу формулаларымен анықталады. Егер 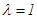болса, яғни 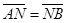онда

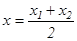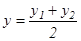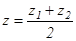, , - кесіндінің ортасын табу формуласы.

Векторлардың скалярлық көбейтіндісі

Анықтама. Екі және векторларының скалярлық көбейтіндісі деп 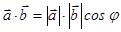санын айтады. Скаляр көбейтінді 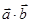, , 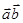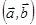символдармен белгіленеді. Мұндағы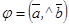 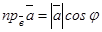( 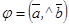), болғандықтан 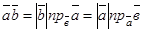деп жазуға болады.

4-мысал. Егер 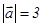, , 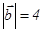, 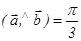онда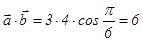

Теорема. базисінде векторының координаталары 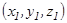, ал векторының координаталары 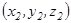болсын. Онда .

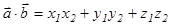5-мысал. Егер 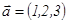, 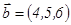болса, онда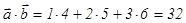

Скалярлық көбейтіндінің қолданылуы

1. 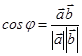немесе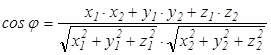

2.

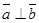
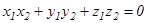
3. 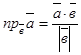( 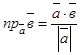) немесе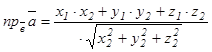

Әдебиеттер:1 нег. [45-65 беттер, 11 қос. [136-156].

Бақылау сұрақтар:

1. Вектор деген не? Векторларға қандай амалдар қолданылады?

2. Вектордың үзындығын қай формуламен есептейді?

3. Кесіндінің қақ ортасын табу формуласын көрсетіңіз.

4. Скаляр көбейтіндінің анықтамасын беріңіз.

5. Скаляр көбейтіндінің механикалық мағынасын түсіндіріңіз

Дәріс.

Дәріс тақырыбы:Векторлық және аралас көбейтінділер.

Дәріс жоспары:

§ Векторлардың векторлық көбейтіндісі.

§ Векторлық көбейтіндінің қасиеттері.

§ Векторлық көбейтіндінің қолданымы.

§ Векторлардың аралас көбейтіндісі.

§ Аралас көбейтіндінің қасиеттері.

§ Жазықтықтағы түзудің теңдеулері.

§ Екі түзудің арасындағы бұрыш.

§ Нүктедентүзуге дейінгі қашықтық.

§ Әдебиеттер.

§ Бақылау сұрақтары.

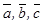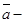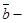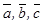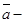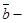Үш компланар емес векторлары берілсін. Егер векторының ұшынан қарағанда дан ға дейінгі ең қысқа бұрылыс сағат тіліне қарсы бағытта орындалса, онда векторлары оң үштік, ал дан ға дейінгі ең қысқа бұрылыс сағат тілімен бағыттас болса, онда 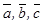сол үштік құрайды дейді.

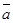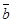Анықтама. және векторларының векторлық көбейтіндісі деп, келесі үш шартты қанағаттандыратын 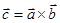векторын айтады:

1) ;

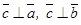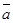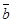2) векторының ұзындығы және векторларына тұрғызылған параллелограммның ауданына тең, яғни 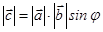, мұндағы ;

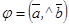3) 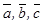векторлары оң үштік құрайды.

Векторлық көбейтінді 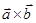немесе 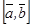деп белгіленеді.

Векторлық көбейтіндінің анықтамасынан 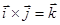, , 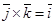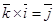болады

Векторлық көбейтіндінің қасиеттері:

1. ;

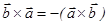2. ;

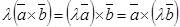3. Нөлдік емес және векторлары 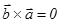жағдайда ғана колинеар;

4. .

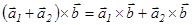Теорема. Егер 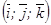базисінде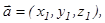 векторлары берілсе, онда .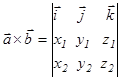

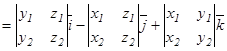1-мысал. 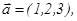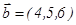векторларының векторлық көбейтіндісін табу керек.

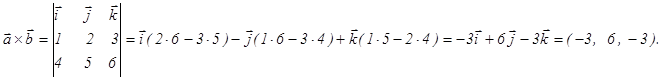Векторлық көбейтіндінің қолданылуы

1. ,

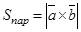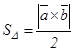
2. Егер 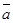|| 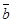болса, онда 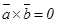(және керісінше)