Основні поняття теорії множин
РОЗДІЛ IІ Множини
Поняття множини належить до категорії найзагальніших, основоположних понять математики. Відповісти на питання «Що таке множина?» не так просто, як це здається на перший погляд. У повсякденному житті та практичній діяльності часто доводиться говорити про деякі сукупності різних об’єктів: предметів, понять, чисел, символів тощо. Наприклад, сукупність сторінок у книзі, сукупність книг у бібліотеці, сукупність об’єктів, які складають основні фонди підприємства, сукупність характерних рис приватного підприємства, сукупність об’єктів і суб’єктів господарської діяльності, сукупність законодавчих актів, які регулюють економічні відносини.
На підставі інтуїтивних уявлень про будь-які подібні чітко визначені сукупності об’єктів сформувалося математичне поняття множини як об’єднання об’єктів у єдине ціле. Саме такої точки зору дотримувався засновник теорії множин німецький математик Георг Кантор. Група математиків, які працювали під псевдонімом Н.Бурбаки, стверджувала: «Множина утворюється з елементів, що мають певні властивості і знаходяться у певних відношеннях між собою чи з елементами інших множин».
Математичне поняття множини пов’язане з абстракцією, яку називатимемо абстракцією множини. Суть її полягає в тому, що всі існуючі властивості і зв’язки предметів не розглядаються, відокремлюються лише одна або кілька властивостей або зв’язків, які виражають належність цих предметів до деякої множини. Якщо ми розглянемо множину співробітників планово-економічного відділу деякої організації, то елементами цієї множини є конкретні люди, які працюють в цьому відділі. Всі властивості цих людей ігноруються за виключенням однієї властивості – бути співробітником планово-економічного відділу. Об’єкти, що утворюють множину, називаються її елементами, або членами. Множина є визначеною, коли можна встановити, чи є будь-який об’єкт її елементом або ні. Наприклад, якщо ми розглядаємо множину студентів групи 1ЕК1, то всі властивості (молодих людей, які складають групу 1ЕК1) і зв’язки з іншими множинами ігноруються, відокремлюється лише зв’язок з групою 1ЕК1, тобто властивість бути саме студентом саме групи 1ЕК1.
Якщо ми розглянемо множину студентів, яка знаходиться кожного вівторка весняного семестру на другій навчальній парі, в аудиторії 402 третього корпусу ХДТУ, то виявиться, що цю множину складають ті самі студенти групи 1ЕК1, що і тільки що розглянуту множину. Хоча для елементів цієї множини основним є зв’язок з певною аудиторією в певний час. Але в цій аудиторії в цей час знаходяться саме студенти групи 1ЕК1, хоча зараз не важливо, що це студенти групи 1ЕК1, важливим є лише те, що ці студенти знаходяться саме в даній аудиторії в даний час, тобто відокремлюється зв’язок саме з аудиторією в даний час. Іншими словами одні й ті самі об’єкти можуть одночасно бути елементами різних множин.
Для позначення конкретних множин використовують великі літери  ,
, 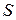 ,
, 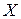 ,... або великі літери з індексами
,... або великі літери з індексами 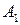 ,
, 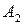 і т. д. Для позначення елементів множин загалом застосовують малі літери
і т. д. Для позначення елементів множин загалом застосовують малі літери 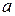 ,
, 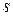 ,
, 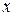 , ... або малі літери з індексами
, ... або малі літери з індексами 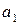 ,
, 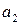 і т.д.
і т.д.
Для позначення того, що 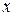 є елементом множини
є елементом множини 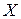 (тобто
(тобто 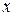 належить
належить 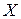 ), будемо застосовувати запис
), будемо застосовувати запис 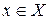 , а запис
, а запис 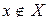 означатиме, що елемент
означатиме, що елемент 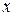 не належить множині
не належить множині 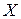 . Записом
. Записом 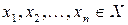 користуються як скороченням для запису
користуються як скороченням для запису 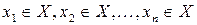 . Символ
. Символ 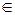 називається символом належності.
називається символом належності.
Приклад 2.1. Наведемо ще кілька прикладів множин:
· Множина натуральних чисел, які є меншими за 15. Позначимо її 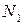 ;
;
· Множина цифр десяткової системи. Позначимо її 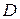 ;
;
· Множина цифр двійкової системи. Позначимо її  ;
;
· Множина парних чисел. Позначимо її 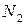 ;
;
· Множина видів навчальних занять студентів. Позначимо її  .
.
Таким чином, ми дійшли проблеми задання множин. При цьому наведені вище приклади множин задають описи характеристичних властивостей, які повинні мати їхні елементи.
Способи подання множин
Є кілька способів подання множин.
1. Вербальний (словесний) за допомогою опису властивостей, які повинні мати елементи множин.
2. Список (перелік) усіх елементів у фігурних дужках.
Приклад 2.2. Стосовно зазначених вище прикладів маємо:
· 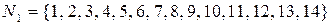 ;
;
· 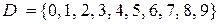 ;
;
· 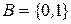 ;
;
· 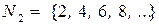 .
.
· 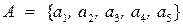 , де
, де
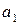 – лекції;
– лекції;
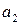 – лабораторні роботи;
– лабораторні роботи;
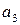 – практичні заняття;
– практичні заняття;
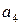 – індивідуальна робота;
– індивідуальна робота;
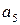 – самостійна робота.
– самостійна робота.
3. Предикатний (висловлювальний, породжувальний) за допомогою предиката, тобто множина задається у вигляді 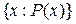 або
або 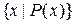 , де
, де 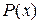 набуває значення «істина» для елементів множини.
набуває значення «істина» для елементів множини.
Приклад 2.3. Приклади предикатів:
· 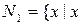 – натуральне число, яке менше за 15};
– натуральне число, яке менше за 15};
· 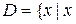 – цифра десяткової системи};
– цифра десяткової системи};
· 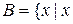 – цифра двійкової системи
– цифра двійкової системи 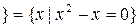 ;
;
· 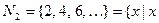 – парне число
– парне число 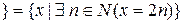 ;
;
· 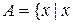 – від навчальних занять студентів}.
– від навчальних занять студентів}.
4. За допомогою породжувальної процедури, яка описує спосіб отримання елементів множини із вже існуючих або інших об’єктів, якщо такий спосіб існує. Елементами множини є всі об’єкти, які можуть бути створені за допомогою цієї процедури. Частіше за все породжуюча процедура задається рекурсивними правилами.
Приклад 2.4. Задамо породжуючі процедури для раніше наведених прикладів:
· для множини 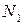 :
:
а) 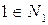 ; б) якщо
; б) якщо 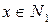 , то
, то 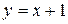 теж
теж 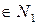 , поки
, поки 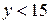 ;
;
· для множини 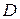 :
:
а) 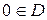 ; б) якщо
; б) якщо 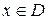 , то
, то 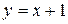 теж
теж 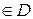 , поки
, поки 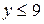 ;
;
· для множини B:
а) 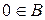 ; б) якщо
; б) якщо 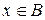 , то
, то 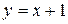 теж
теж 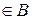 , поки
, поки 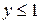 ;
;
· для множини 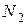 :
:
а) 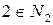 ; б) якщо
; б) якщо 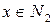 , то
, то 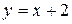 теж
теж 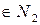 ;
;
· для множини  породжуючої процедури не існує, тому що не зрозуміло яким чином можна отримати наступний елемент із вже існуючих.
породжуючої процедури не існує, тому що не зрозуміло яким чином можна отримати наступний елемент із вже існуючих.
5. Аналітичний (за допомогою формул). Про цей спосіб далі.
Із наведених прикладів випливає, що множини бувають скінченими та нескінченними. Множини називають скінченими, якщо число їх елементів скінчене, тобто існує натуральне число 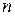 , яке є числом елементів множини. Множини називають нескінченними, якщо вони містять нескінченне число елементів.
, яке є числом елементів множини. Множини називають нескінченними, якщо вони містять нескінченне число елементів.
Введені вище поняття теорії множин з успіхом можуть бути використані в основах аналізу, алгебрі, математичній логіці, економіці та ін. Однак при більш строгому розгляді такі інтуїтивні уявлення можуть виявитися незадовільними. Недосконалість інтуїтивних уявлень про множини, їх недостатність ілюструється, наприклад, відомим парадоксом Б.Рассела, який формулюється таким чином. Розглянемо множину  всіх таких множин
всіх таких множин 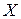 , що
, що 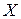 не є елементом
не є елементом 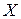 . Тоді, якщо
. Тоді, якщо  не є елементом
не є елементом  , то за означенням
, то за означенням  також є елементом
також є елементом  . З іншого боку, якщо
. З іншого боку, якщо  є елементом
є елементом  , то
, то  – одна з тих множин
– одна з тих множин 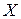 , які не є елементами самих себе, тобто
, які не є елементами самих себе, тобто  не є елементом
не є елементом  . У будь-якому випадку
. У будь-якому випадку  є елементом
є елементом  й
й  не є елементом
не є елементом  . Парадокс Рассела частіше за все формулюють у вигляді запитання: “Чи голить себе цирульник, який голить тих, хто не голиться сам?”, на яке не існує відповіді. Цей парадокс ще називають парадоксом лжеца.
. Парадокс Рассела частіше за все формулюють у вигляді запитання: “Чи голить себе цирульник, який голить тих, хто не голиться сам?”, на яке не існує відповіді. Цей парадокс ще називають парадоксом лжеца.
Цей парадокс свідчить про те, що теорія множин, яка широко використовується в її інтуїтивному, «наївному» викладі, є суперечливою. Формалізація теорії множин, пов’язана, зокрема, з усуненням парадоксів, сприяла розвитку не тільки методів теорії множин, а й математичної логіки.
Приклад 2.5.Наведемо приклади інших множин:
За колишньою марксистською класифікацією функціональною основою розвитку людського суспільства є матеріальне виробництво, яке як множина, позначимо її  , складається з трьох елементів, які теж є множинами:
, складається з трьох елементів, які теж є множинами: 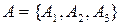 , де
, де
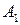 – множина робочих ресурсів,
– множина робочих ресурсів,
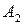 – множина предметів праці,
– множина предметів праці,
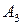 – множина засобів праці.
– множина засобів праці.
В свою чергу 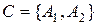 множина, яка називається множиною продуктивних сил.
множина, яка називається множиною продуктивних сил.
Множина  засобів виробництва складається з двох елементів:
засобів виробництва складається з двох елементів: 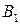 – множини предметів праці і
– множини предметів праці і 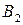 – множини засобів праці:
– множини засобів праці:
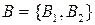 .
.
За ринковою класифікацією, яка панує зараз, множина економічних ресурсів 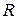 , тобто ресурсів, які використовуються для виробництва товарів і послуг, складається з двох елементів:
, тобто ресурсів, які використовуються для виробництва товарів і послуг, складається з двох елементів:
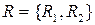 , де
, де
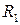 – множина матеріальних ресурсів,
– множина матеріальних ресурсів,
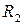 – множина людських ресурсів.
– множина людських ресурсів.
Порожня множина
У теорії множин використовується поняття порожньої множини. Позначається вона символом Æ.
Множина може взагалі не містити елементів, наприклад
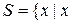 – непарне число, що ділиться на
– непарне число, що ділиться на 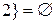 ;
;
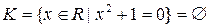 .
.
Для позначення цього факту вводиться поняття порожньої множини.
Це поняття відіграє дуже важливу роль при заданні множин за допомогою опису. Так, без поняття порожньої множини не можна говорити про множину відмінників групи 1ЕК спеціальності “Економічна кібернетика” або про множину дійсних коренів квадратного рівняння, не пересвідчившись заздалегідь, чи є взагалі в студентській групі відмінники або чи має задане рівняння дійсні корені. Поняття порожньої множини дає змогу оперувати множиною відмінників групи, не піклуючись про те, чи є відмінники в групі, яка розглядається. Теж саме стосується й множини дійсних коренів квадратного рівняння. Порожню множину умовно будемо відносити до скінченних множин. Можна довести, що порожня множина єдина.
Таким чином, уведення порожньої множини дає можливість оперувати будь-якою множиною без попереднього застереження, існує вона чи ні.
Операції над множинами
Розглянемо дві множини А та В і введемо кілька операцій над ними. Для графічної ілюстрації будемо використовувати кола Ейлера. Для зображення множини на площині креслять замкнену лінію із заштрихованою внутрішньою областю (найчастіше – це коло, звідси й назва відповідного інструмента, що широко застосовується в теорії множин).
Зазначимо, що в подальшому викладі використовуватимемо символи вже відомих нам логічних операцій кон’юнкції « 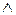 » диз’юнкції «
» диз’юнкції « 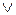 » імплікації «
» імплікації « 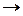 », еквіваленції «
», еквіваленції « 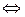 » для формалізованого запису означень і теорем.
» для формалізованого запису означень і теорем.
Означення 2.1. Об’єднання  і
і  (
( 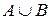 ) – множина, що складається з усіх елементів множини
) – множина, що складається з усіх елементів множини  , всіх елементів множини
, всіх елементів множини  і не містить ніяких інших елементів (рис.2.1), тобто
і не містить ніяких інших елементів (рис.2.1), тобто
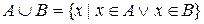 ,
,
де символ « 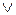 » позначає логічну операцію диз’юнкції (логічне «або»), тобто, згадуючи операцію „диз’юнкція”, елемент
» позначає логічну операцію диз’юнкції (логічне «або»), тобто, згадуючи операцію „диз’юнкція”, елемент 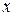 належить множині
належить множині 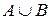 тоді і тільки тоді, коли або
тоді і тільки тоді, коли або
1. 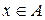 істинне і
істинне і 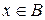 хибне, або
хибне, або
2. 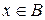 істинне і
істинне і 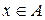 хибне, або
хибне, або
3. 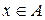 істинне і
істинне і 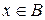 істинне.
істинне.
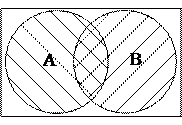
Рис.2.1
Означення 2.2. Переріз  і
і  – множина, що складається з тих і тільки тих елементів, які належать одночасно множині
– множина, що складається з тих і тільки тих елементів, які належать одночасно множині  та множині
та множині  (рис.2.2), тобто
(рис.2.2), тобто
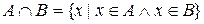 ,
,
де символ « 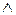 » позначає логічну операцію кон’юнкції (логічне «і»), тобто згадуючи операцію „кон’юнкція”, елемент
» позначає логічну операцію кон’юнкції (логічне «і»), тобто згадуючи операцію „кон’юнкція”, елемент 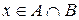 тоді і тільки тоді, коли
тоді і тільки тоді, коли 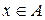 і
і 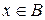 істинні одночасно.
істинні одночасно.

Рис.2.2
Означення 2.3. Різниця  і
і  (відносне доповнення) – множина, що складається з тих і тільки тих елементів, які належать множині
(відносне доповнення) – множина, що складається з тих і тільки тих елементів, які належать множині  й не належать
й не належать  (рис.2.3), тобто
(рис.2.3), тобто
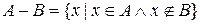 .
.
Тобто, елемент 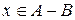 тоді і тільки тоді, коли
тоді і тільки тоді, коли 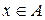 істинне і
істинне і 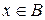 хибне одночасно.
хибне одночасно.
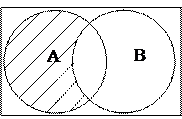
Рис.2.3
Означення 2.4. Диз’юнктивна сума  і
і  (симетрична різниця) – множина, що складається з усіх елементів
(симетрична різниця) – множина, що складається з усіх елементів  , які не належать множині
, які не належать множині  , й усіх елементів
, й усіх елементів  , які не належать множині
, які не належать множині  , та яка не містить ніяких інших елементів (рис.2.4), тобто
, та яка не містить ніяких інших елементів (рис.2.4), тобто
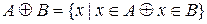 .
.
Тобто, елемент 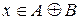 тоді і тільки тоді, коли або
тоді і тільки тоді, коли або
1. 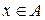 істинне і
істинне і 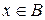 хибне одночасно, або
хибне одночасно, або
2. 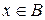 істинне і
істинне і 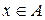 хибне одночасно.
хибне одночасно.
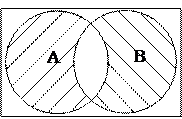
Рис.2.4
Очевидно, що
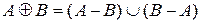 .
.
Вправа 2.1.
1. Задати всіма можливими способами множини:
1. непарних чисел, які є меншими за 20;
2. всіх непарних чисел;
3. цифр вісімкової системи зчислення;
4. чисел, кратних 5;
5. чисел, кратних 7;
6. парних чисел, які є більшими за 10;
7. парних чисел, які є меншими за 100;
8. чисел, кратних 3 і 5 одночасно;
9. чисел, кратних 4 і 7 одночасно;
10. квадратів натуральних чисел;
11. квадратів парних чисел;
12. квадратів непарних чисел.
2.1.4. Універсум 
Звичайно, вже в контексті деякої задачі, в якій виникає конкретна множина, явно або неявно обмежується сукупність об’єктів, що є допустимими (натуральні числа – серед цілих або дійсних залежно від контексту, студенти – серед студентів факультету, університету, або серед всіх студентів України, або світу залежно від контексту).
Зручно сукупність допустимих об’єктів зафіксувати явно, як деяку множину та вважати, що множини, які розглядаються, складаються з елементів цієї множини. Її називають основною множиною (універсумом) і позначають 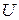 .
.
Наприклад, універсумом 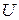 для множин, які виникають в деякій арифметичній задачі, є числа (залежно від контексту натуральні, цілі, дійсні або комплексні). Універсумом
для множин, які виникають в деякій арифметичній задачі, є числа (залежно від контексту натуральні, цілі, дійсні або комплексні). Універсумом 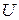 для множин деякої задачі, що стосується зоології, є множина тварин (залежно від контексту це множина всіх тварин або ссавців, або птахів і т.д.).
для множин деякої задачі, що стосується зоології, є множина тварин (залежно від контексту це множина всіх тварин або ссавців, або птахів і т.д.).
Приклад 2.6. Якщо в задачі мова іде про студентів, то універсумом 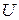 може бути множина всіх студентів деякої групи, або факультету, або деякого університету, або всіх ВНЗ України, або всього світу. Наприклад, якщо в задачі підраховується успішність деякого окремого студента групи 1ЕК, то в якості
може бути множина всіх студентів деякої групи, або факультету, або деякого університету, або всіх ВНЗ України, або всього світу. Наприклад, якщо в задачі підраховується успішність деякого окремого студента групи 1ЕК, то в якості 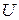 достатньо обрати множину студентів цієї групи, якщо складається порівняльна таблиця успішності студентів першого курсу КНЕУ або ХДТУ, то в якості універсуму
достатньо обрати множину студентів цієї групи, якщо складається порівняльна таблиця успішності студентів першого курсу КНЕУ або ХДТУ, то в якості універсуму 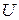 достатньо розглядати множину всіх студентів першого курсу даних навчальних закладів.
достатньо розглядати множину всіх студентів першого курсу даних навчальних закладів.
Будь-яку множину розглядатимемо у зв’язку з універсумом, який на колах Ейлера асоціюватимемо з прямокутником на площині, всередині якого зображатимемо множини, як ми робили, починаючи з рис.2.1.
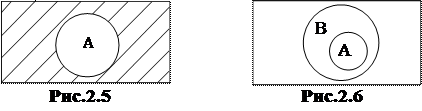
Нова операція 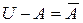 – (абсолютне доповнення
– (абсолютне доповнення  ) – це множина, що містить усі елементи універсуму, за винятком елементів
) – це множина, що містить усі елементи універсуму, за винятком елементів  (рис.2.5).
(рис.2.5).
Приклад 2.7. Якщо розглядати в якості універсуму 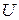 множину співробітників деякої фірми та означити літерами:
множину співробітників деякої фірми та означити літерами:
·  – множину менеджерів цієї фірми;
– множину менеджерів цієї фірми;
·  – множину співробітників за віком більш 30 років;
– множину співробітників за віком більш 30 років;
· 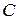 – множину співробітників за віком більш 40 років;
– множину співробітників за віком більш 40 років;
· 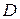 – множину співробітників, які мають стаж роботи більш за 5 років.
– множину співробітників, які мають стаж роботи більш за 5 років.
Визначимо зміст множин:
1) 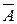 – множина співробітників фірми, які не є менеджерами;
– множина співробітників фірми, які не є менеджерами;
2) 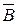 – множина співробітників фірми, яким за віком не більше 30 років;
– множина співробітників фірми, яким за віком не більше 30 років;
3) 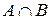 – множина менеджерів фірми, яким за віком більш 30 років;
– множина менеджерів фірми, яким за віком більш 30 років;
4) 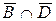 – множина співробітників фірми за віком не більш 30 років, які мають стаж роботи не більш 5 років;
– множина співробітників фірми за віком не більш 30 років, які мають стаж роботи не більш 5 років;
5) 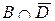 – множина співробітників фірми за віком більш 30 років, які мають стаж роботи не більш 5 років.
– множина співробітників фірми за віком більш 30 років, які мають стаж роботи не більш 5 років.
