Цикл Карно в Т,s-координатах

На рис. 3.19 в Т,s-координатах изображен цикл Карно, состоящий из двух изотерм (T = const) и двух адиабат (s = const). Теплота 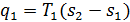, подведенная к рабочему телу от теплоисточника при температуре Т₁, эквивалентна согласно формуле площади прямоугольника s₁АВs₂. А теплота 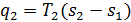, отданная теплоприемнику, – площади прямоугольника s₁DCs₂ . Следовательно, работа цикла l_ц = q₁– q₂эквивалентна площади прямоугольника ABCD. Тогда из формулы h_t=1- q₂/q₁ и рис. 3.19 непосредственно следует, что термический к.п.д. цикла Карно равен:

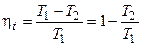
и не зависит от природы и свойств рабочего тела, поскольку никаких предположений об этом при изображении данного цикла в T, s-координатах не делалось.

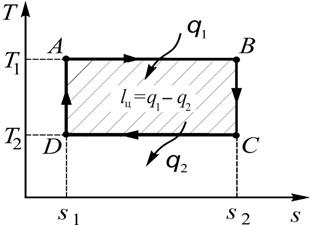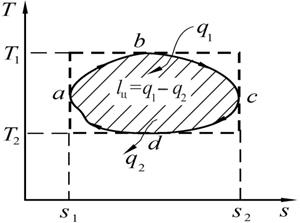Рис. 3.19. Цикл Карно	Рис. 3.20. Сравнение произвольного цикла с циклом Карно

Используя Т, s-координаты, можно в наглядной форме привести доказательство и второй теоремы Карно, гласящей, что невозможно создать тепловую машину, работающую в том же диапазоне температур (между Т₁ и Т₂ ), термический КПД которой был бы выше КПД цикла Карно.

Действительно, пусть в некотором диапазоне температур между Т₁ и Т₂ осуществлён некоторый произвольный цикл, изображенный сплошной замкнутой кривой на рис. 3.20. Окружим его циклом Карно, работающим в том же

диапазоне температур и изображенным на рис 3.20 жирными штриховыми линиями. Теплота 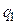, сообщенная рабочему телу в процессе a-b-c данного произвольного цикла (эквивалентная площади под кривой a-b-c), не может быть больше, чем была бы сообщена тому же рабочему телу в цикле Карно при Т = Т₁ (в том же диапазоне увеличения энтропии), т.е. .

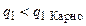Аналогично теплота 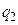, отданная рабочим телом в произвольном цикле в процессе c-d-a, не может быть меньше, чем в рассматриваемом цикле Карно:

.

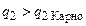Так как в произвольном цикле 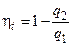, а в цикле Карно

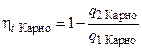, то, учитывая, что 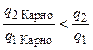, получим .

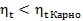3.9. i,s - координаты

Недостатком диаграмм, построенных в Т,s - координатах является необходимость вычислять площади отдельных участков диаграммы при определении теплотыq и работы l процесса, изменения внутренней энергии Δu и энтальпии Δi газа. Этого недостатка лишены диаграммы состояния, построенные в i,s - координатах(энтальпия - энтропия), где величиныq, l, Δu и Δiоделяются по отрезкам прямых. Данная особенность i,s-координат упрощает анализ и расчет термодинамических про­цессов.

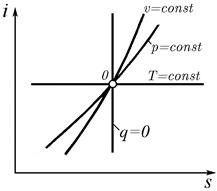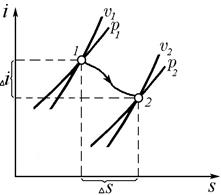Рис. 3.21. Основные процессы в i,s-координатах	Рис. 3.22. Фрагмент i,s-диаграммы

Рассмотрим протекание основных процессов с идеальными газами в i,s-координатах (рис. 3.21).

Обратимый адиабатный процесс изображается в координатах i,s, как и в координатах Т,s, прямой вертикальной линией (s = const).

Изотермический процесс. Для идеального газа

.

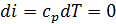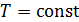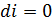Так как в этом процессе , то . Следовательно, 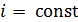– это горизонтальная линия в i,s-координатах.

Изобарный процесс. Здесь

.

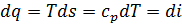Изобара представляет собой кривую линию, тангенс угла накло­на касательной к которой равен: .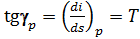

Так как в изобарном процессе с ростом энтальпии увеличивает­ся температура газа Т, то возрастает и 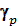. Следовательно, как и в Т, s-координатах, изобара обращена выпуклостью к оси абс­цисс.

Изохорный процесс. По аналогии с изобарным процессом можно записать ,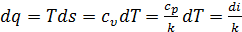

отсюда .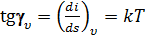

Следовательно, изохора так же, как и изобара, представляет со­бой кривую линию, обращенную выпуклостью к оси абсцисс. Взаимное расположение изобары и изохоры в i,s-координатах (см. рис. 3.21) аналогично с их расположением в T,s- координатах.

С помощью i,s-диаграммы (рис. 3.22) можно определить основные термодинамические величины, входящие в формулу первого закона термодинамики. Зная положение точек начала 1 и конца2 процесса, непосредственно из диаграммы определяют­ся параметры газа в этих точках p₁,υ₁, p₂,υ₂, кроме того, 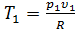и 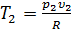. Изменение энтальпии и энтропии также непосредственно определяется из диаграммы, т.е. 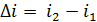и .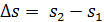

Изменение внутренней энергии определим по формуле

.

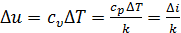Тогда величины теплоты и работы в различных процессах опре­деляются следующим образом:

- в изобарном процессе , ;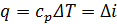

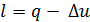- в изохорном процессе ;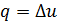

- в изотермическом процессе , ;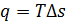

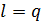- в адиабатном процессе 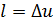.