Исықсызықты интегралдың қасиеттері

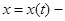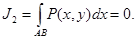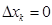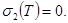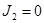тұрақты шама болсын.Онда Шынында да, кез келген T бөлінуі үшін болғандықтан шама болса, онда Бұдан болатыны шығады.

Теорема 27.( Риман интегралы арқылы Қисықсызықты интегралдың мәнін есептеу).

g(x,y) функциясы L-де үзіліссіз болсын.Онда 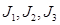қисықсызықты интегралдар табылады және сәйкесінше

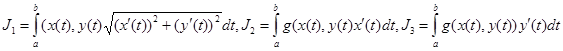тең.Дәлелденді.

Алдымен 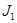интегралын қарастырамыз. 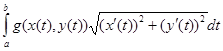интегралы үшін 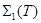интегралдық қосынды ,қисықсызықты интегралдың 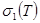интегралдық қосындысынан 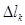- ның орнына онда кейбір 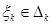кезінде 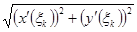шамасының тұруымен ерекшеленеді, яғни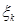

нүктесінде алынған және t айнымаланың 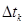өсімшесіне жауап беретін қисықтың доға ұзындығының дифференциалы.Ары қарай,Стильтес интегралының анықтамасына жүгінуге болады: 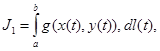мұндағы 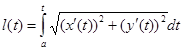және сонымен бірге интегралдардың теңдігін дәлелдеуді аяқтауға болар еді, бірақ біз осы фактының тікелей дәлелдеуін береміз.[a,b] кесіндісіндегі 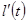туындысының үзіліссіздігіне байланысты онда оның бірқалыпты үзіліссіздігін аламыз.Сонда кез келген 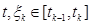нүктелері үшін 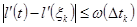аламыз,әрі 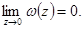Бұдан 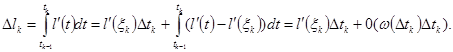g(x,y) функциясы L компактысында үзіліссіз болғандықтан,ол онда шектелген,яғни мынадай 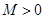табылады да ,кез келге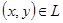н үшін 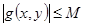болады.

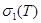интегралдық қосындысын түрлендіріеміз .Мынаны аламыз:

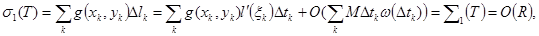
Мұндағы .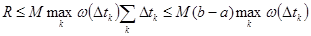

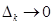кезде 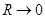болғандықтан,онда бұл 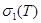және 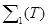бірмезетте жинақталатынын және бір және шегі болатынын білдіреді.Дәлелденді.

Теорема 27. Қисықсызықты интегралдардың мәнін есептеудің әмбебап әдісін береді.Осы теореманың салдарынан қисықсызықты интегралдардың Риман интегралға жай көшуінен алынады.

Салдар 1.Келесі теңдік дұрыс:

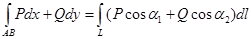мұндағы 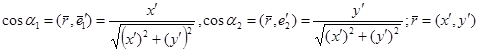L қисығының (x,y) нүктесіндегі жанама векторы ; 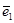және 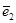- Ox және Oy координат остері бойынша бағытталған ,бірлік орттар.

Салдар 2.Егер кез келген 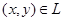нүктесі үшін 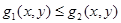теңсіздігі дұрыс болса,онда 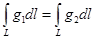аламыз.

Салдар 3. 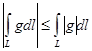теңсіздігі орындалады.

Салдар 4.Егер g функциясы L қисығында үзіліссіз болса,онда мынадай 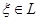нүктесі табылады да, 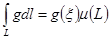болады, мұндағы 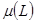- L қисығының ұзындығы.Бірінші және екінше текті интегралдардың мәндері параметрлеуді таңдаудан тәуелді емес , өйткені одан оларды анықтаудың интегралдық қосындысынан тәуелді емес.Дербес жағдайда , 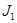интегралы А және B нүктесінің қайсысы басы,ал қайсысы L қисығының соңы екендігіне тәуелді емес (бұл жағдайда параметрлеуді ,мысалы , 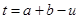қатысымен анықтауға болады),Сонымен бірге , 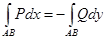теңдігінің орны бар ,яғни интегралдың мәні L қисығын айналып өту бет бағытын таңдаудан тәуелді.

L қисығының екі параметрлеуін қарастырамыз:

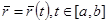және – бұл [а₁ , b₁] кесіндісінің [а , b] кесіндісінде тегіс бейнелеуі болсын.

Онда , 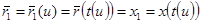аламыз. 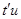туындысының [a,b] кесіндісінің барлық жерінде бір және тек сол ғана таңбаға ие болатынын , атап өтейік . Қарсы жағдайда , Вейерштрасс теоремасы бойынша мынадай 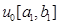нүктесі табылады да , 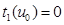болады . Бірақ , онда 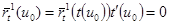және L қисығының ерекше нүктесі бар , яғни ол ерекшеленген болады , ол негізінде ол бұлай емес .

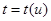бейнелеуі кезінде [a₁ ,b₁] кесіндісінің шектік нүктелері , 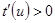кезінде [a ,b] кесіндісінің шектік нүктелеріне көшетін болғандықтан , 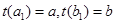. Шынында да , Лагранж теоремасынан кейбір 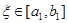кезінде 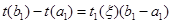аламыз . Олай болса , 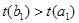, ал бұл 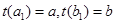, болатынын білдіреді . Ары қарай Теорема 27 және Риман интегралындағы айнымалыны алмастыру туралы теореманы пайдаланамыз . Келесі теңдіктер тізбесін аламыз :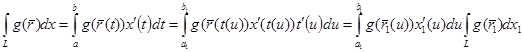

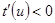жағдайында 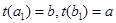аламыз . Алдыңғы пайымдауды қайталап , бұл жағдайда бір параметрлеуден басқа параметрлеуге көшу кезінде келесі теңдіктің дұрыстығын аламыз: .

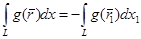Өлшемділігі екіден жоғары кеңістіктегі қисықсызықты интеграл үшін ұқсас қасиеттердің орны бар . Мысалы , үшөлшемді жағдайда 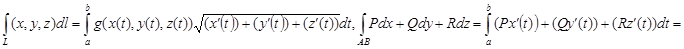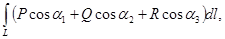мұндағы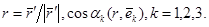

Мысал . 1)Эллипс бойынша 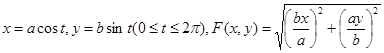, функциясынан I-текті интегралдарды есептеу керек .

.

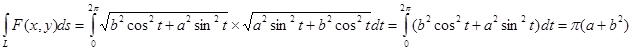2) 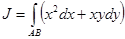екінші текті интегралды (1.1) нүктесіне жүргізілген түзусызықты

кесінді бойымен және осы нүктелерді қосатын 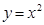параболасының доғасы бойынша есептеу керек . Бірінші жағдайда (y=x) мынаны аламыз:

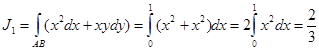.Екінші жағдайда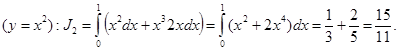

Қос интегралдан қайталанғанға ауысу

Қос және қайталанған интегралдардың теңдігі туралы теореманы құрайық.

Теорема 7. Функция 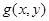тіктөртбұрыш 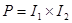, 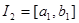-де интегралданатын болсын. Сол сияқты бір айнымалылы у-тің 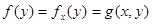функциясының ке-келген бекітілген 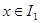мәні үшін, 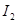кесіндісінде у бойынша интегралданады және 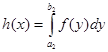. Сонда мына формуланың орны бар:

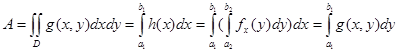яғни қос интеграл қайталанған интегралға тең. Дәлелдеуі.

Тіктөртбұрыш Р-ның кез-келген T=T_p бөлінуі үшін.

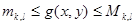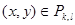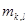теңсіздігін аламыз, мұндағы және мен 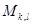k=1, …,m;

l=1, …,n шамаларының дағдылы мағынасы бар.

Бекітілген 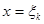кезінде бұл теңдікті 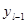-ден 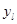-ге дейін у бойынша интегралдаймыз. Сонда

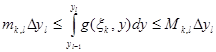
Бұл теңсіздікті l бойынша қарстырамыз.

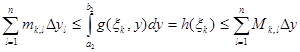
Соңғы теңсіздікті 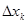-ға көбейтіп және оны к бойынша қосып, мынаны аламыз:

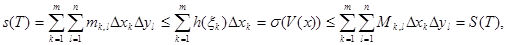
Мұндағы V(x)-I₁ кесіндісінің Т бөлінуінің белгісі. Одан басқа

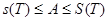
Функция 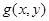Р-да интегралданатын болғандықан, онда кез-келген 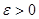саны үшін, мынандай 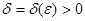саны табылады да, 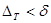шартымен әрбір Т бөліну үшін , 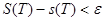болады. Бөліну 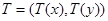бөліну жұбынан құрылған: T(x)-Ox осі бойынша, T(y)- Оу осі бойынша. Бөліну T(x) ретінде 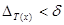шартымен кез-келген бөлінуді алуға болады. Бөліну T(x) –тың кез-келген белгісін аламыз. I₁ кесіндісінің V=V(x) ұсақталған бөлінуін аламыз.

А және 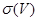сандарының екеуі де ұзындығы 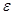-ға тең бір кесіндіде жатады және 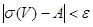. Бұл теңсіздік 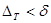шартымен кез-келген ұсақталған бөліну үшін дұрыс. Олай болса, мына теңдіктің орны бар:

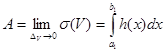
Дәлелденді.

Кез-келген өлшенген D жиыны бойынша интегралдау жағдайы қарастырылғаннан айырмашылығы аз. Тіктөртбұрыш Р D-ны қамтитын болсын. Сонда анықтама бойынша

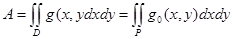болады, мұндағы 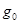функциясы D жиынында g функциясымен сәйкес және D-ның сыртында 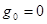, 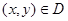үшін у нүктелерінің жиынын E(x) арқылы белгілейміз. E(x) жиыны 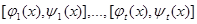кесінділерінің шектеулі санынан тұрады. Сонда егер 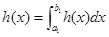, мұндағы

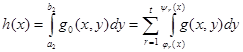
Формуласының орны бар және ол теорема 7-нің тұжырымын жалпылайды.

Қос интегралдың негізгі қасиеттері

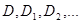-Жордан бойынша өлшенетін жиын және 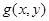, , 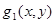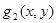функциялары қарстырылатын жиындағы Риман бойынша интегралданады. Онда келесі қасиеттер орынды болады.

1) Мына теңдіктер дұрыс:

a)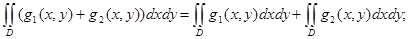

б) 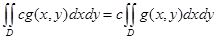, 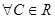(сызықтық қасиеті).

2) g₁ және g₂ функциялары D-да интегралданатын болсын, онда g₁g₂ D-да интегралданады.

3) D-да 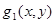≤ 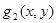теңсіздіктері дұрыс болсын. Бұл жағдайда:

a) 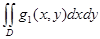≤ 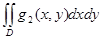(монотонды қасиеті)

б) D-да сондай-ақ 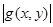интегралданатын болсын. Онда ≤

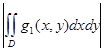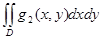
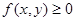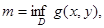
в) , 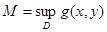болсын. Онда мынадай m<c<M, c саны табылып,

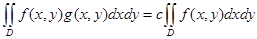
(орта туралы теорема)

4) .

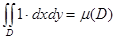Бұл тұжырым Жордан өлшемінің және жалпыланған қос интеграл анықтамалаының эквиваленттілігінен шығады.

5) Егер 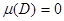болса, онда D- да шектелген кез-келген 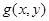функциясы үшін

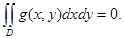
Дәлелденуі: Функция 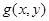D жиынында шектелген болғандықтан, онда мынадай M>0 саны табылады да, барлық 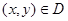нүктелері үшін 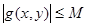теңсіздігі орындалаы. 3), 1) және 4) қасиеттерден мынаны аламыз:

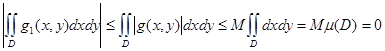. Дәлелденді.

6) Облыстар D₁ және D₂-нің ортақ ішкі нүктелері жоқ болсын. Онда 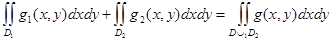(аддитивтілік қасиеті)

Дәлелденуі: Стандартты тіктөртбұрыш D₁ және D₂ қамтитын болсын. Онда анықтама бойынша

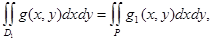
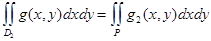
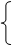Мұндағы: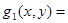

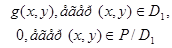
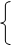
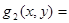
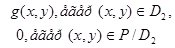
Бұдан және интегралдың сызықтық қасиетінен мынаны аламыз:

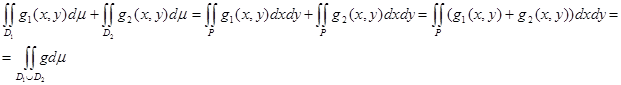Дәлелденді.

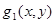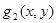7) Егер және функцияларының мәндері D₁ жиынында ғана айырмашылығы болса, әрі 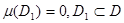онда

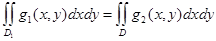
Дәлелденуі.Шындығында да,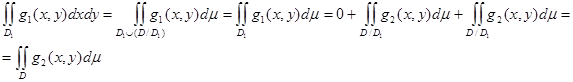

Лебег критерийі

Теорема 21.(Лебег критерийі). Шектелген 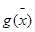функциясы Р тіктөртбұрышында Риман бойынша интегралданады, сонда тек сонда ғана, егер оның үзіліс нүктелерінің D жиынының Лебегтік нөлдік мөлшері бар болса.

Дәлелдеуі: Қажеттілігі. Теорема 20 бойынша D(1/n) жиынының кез-келген натурал n саны үшін ,лебегтік нөлдік мөлшері бар болады. Бұдан Лебегтік мөлшері 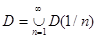нөлге тең дегенді аламыз.

Қажеттілігі:Кез-келге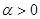н үшін 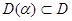болады. Сондықтан, егер мөлшер 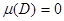болса, онда 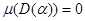. Теорема 20 дан 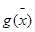функцияның тіктөртбұрышында интегралданатыны шығады. Дәлелденді.

Теорема 22. Функция 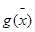тіктөртбұрышта интегралданатын болсын. 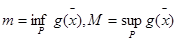және 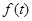функциясы 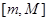кесіндісінде үзіліссіз болсы. Онда 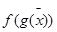функциясының үзіліссіздік нүктсі болады. Олай болса, g функциясының үзіліс нүктесі 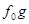үзіліс нүктесі болуы мүмкін. Сондықтан 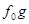үзіліс нүктесінің жиыны нөлдік мөлшеден жиынның ішкіжиыны ретінде Лебегтің нөлдік мөлшері болады.(Лебег критерийі бойынша 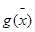үзіліс нүкте жиынының мөлшері нөлге тең). Дәлелденді.

Потенциалды және соленоидалды векторлық

Анықтама 21. Егер мынадай 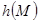скалярлық функциясы табылады, 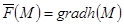болса, онда 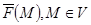векторлық өрісі 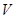облысында потенциалдық, ал 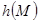функциясының өзі онда 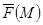векторлық өрісінің потенциалы деп аталады. Егер 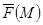шамасын, 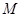нүктесінде сынамалы нүктелік бірлік массасына әсер ететін күш ретінде қарастырсақ, онда 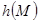потенциалы осы нүктелік массаның шексіздіктен 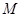нүктесіне орын ауыстыруы бойынша жұмыстың маңызы бар болады. Шынында да, 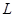қисығы бастапқы 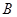нүктесімен және айнымалы 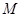нүктесімен берілген болсын. 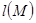арқылы осы қисықтың 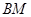доғасының ұзындығын, ал 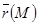арқылы оған 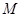нүктесінде жүргізілген бірлік жанама векторды белгілейміз. Сонда 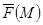күшінің сынамалы массасының орын ауыстыруы бойынша .
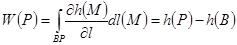Анықтама 22. Тұйық 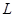контуры бойынша 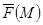векторлық өрісінің циркуляциясы деп 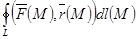шамасын айтамыз. Алдыңғы өрнектен 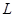контуры бойынша 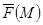күшінің 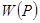жұмысы үшін мынаны аламыз, яғни кез келген тұйық түзетілген контур бойынша потенциалдық өрістің циркуляциясы нөлге тең.
Теорема 12. Дөңес 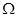облысында тегіс векторлық өріс потенциалдық болуы үшін, мына эквиваленттік шарттардың біреуінің орындалуы қажетті және жеткілікті:
1) кез келген бөлікті-тегіс тұйық 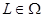қисығы үшін ;
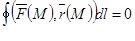2) .
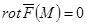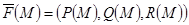бейнелеуі үшін, анықтамаға байланысты мына теңдіктің орны бар:
.
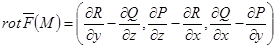Анықтама 23. Егер мынадай 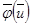векторлық өрісі табылады, 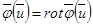болса, онда 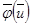векторлық өрісі соленоидалдық (немесе трубалық), ал 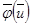векторлық өрісі 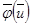өрісінің векторлық потенциалы деп аталады.
Теорема 13. 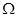-дөңес компакт болсын. Векторлық 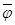өрісі соленоидалдық болуы үшін 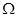-ның барлық нүктелері үшін, 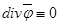теңдігінің орындалуы қажетті және жеткілікті. Дәлелдеуі.
Қажеттілігі. 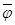өрісі соленоидалды, олай болса 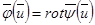. Кез келген векторлық 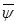өрісі үшін 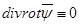теңдігі дұрыс болғандықтан, 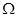облысында 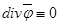аламыз. Қажеттілігі дәлелденді.
Жеткіліктілігі. Енді 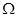облысында 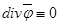болсын. Мынадай 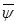векторлық өрісі табылады, 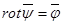болатынын дәлелдейік. 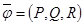векторлық өрісіне сәйкестікке дифференциалдық форманы қоямыз
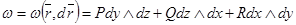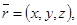
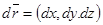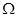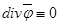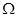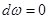, . Сонда -дағы шарты, -дағы шартына эквивалентті. Ал 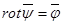теңдігін қанағаттандыратын 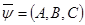векторлық өрісінің бар болу шарты, мынадай 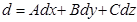дифференциалдық форма табылады, 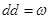болатынын білдіреді. 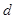формассын мына түрде қарастырамыз:
.
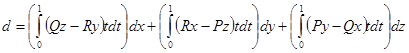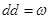екенін дәлелдейік. Теңдіктен мынаны шығарамыз: 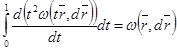. Форманың сызықтылығына байланысты тек қана бір қосылғышты 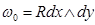қарастыру жеткілікті. Сонда 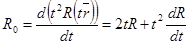. 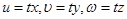деп ұйғарып, мынаны аламыз:
.
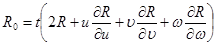Одан әрі, 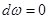қолданамыз, яғни 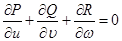. Сонда,
.
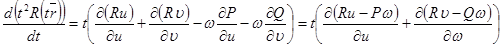Бұдан 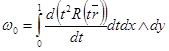. 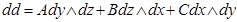болсын. 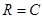болатынын дәлелдеу жеткілікті. 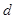форманың анықтамасынан мынаны аламыз:
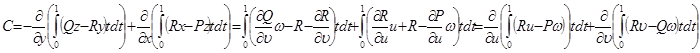Дәлелденді.
Мысал. 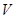-кейбір дөңес Жордан бойынша өлшемді компакт болсын және 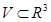. Кез келген 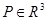бекітілген нүктесі үшін және кез келген 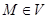нүктесінде радиус-векторды анықтаймыз:
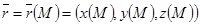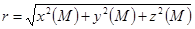, және 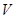облысының 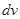көлемінің элементін мына түрде аламыз: 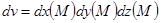. 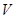облысында 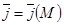векторлық өрісі берілген болсын. Онда 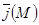векторлық өрісінің 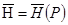күштік өрісін келесі формула бойынша анықтауға болады: 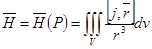. Кез келген 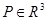нүктесінде 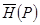күштік анықталады. 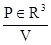жағдайында 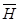өрісін беретін интеграл тегіс функцияның кәдімгі Риманның үш еселі интегралын береді. Егер де 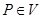болса, онда осы интеграл меншіксіз болады және оның жинақтылығы салыстыру ережесімен шығады (бұл үшін 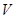облысын центрі 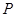нүктесінде орналасқан және радиусы 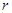шарлық қабаттарға 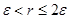, 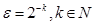шартымен бөлуге болады. 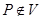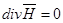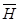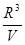Кез келген нүктесі үшін теңдігінің орны бар екенін, яғни теорема 13-ке байланысты өрісі облысында соленоидалды болатынын көрсетеміз. Шынында да, егер 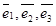- тікбұрышты координат жүйесінде 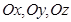координат өстері бойынша бағытталған орттар, 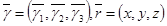болса, онда

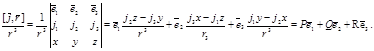
Бұдан

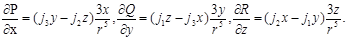
Олай болса,

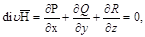
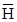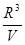яғни өрісі облысында соленоидалды болады. Енді 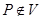кезінде 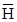өрісінің векторлық потенциалы 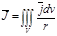векторлық өрісі болатынын яғни 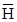өрісі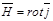

түрінде берілетінін көрсетейік. Интеграл астындағы функцияның тегістігіне байланысты 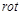операторын қолдану барысы тәртібін және үш еселі интегралды ауытыруға болады. Сонда, 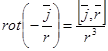дәлелдеу жеткілікті. Шынында да мынаны аламыз:
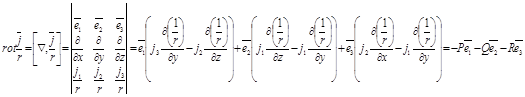мұндағы 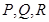функциялары жоғарыда анықталған.

Риман критерийі

Стокс формуласы

Грин формуласы тек жазық жағдайда ғана емес, сондай ақ үш өлшемді кеңістік үшін де дұрыс.Оны Стокс формуласы деп айтады.

Т4. Д-бұл 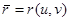бейнелеуі кезіндегі жазық дөңес Д жиының бейнесі, әрі оның координаттары екі рет үзіліссіз дифференциалданатын функция болатын ,

-тегі тегіс өзгешеленбеген кеңістік болсын.

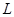қисығы 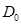жиынының бөліктік –тегіс шекаралары болатын Д бетінің –тегіс шекарасы болсын. 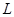шекараларын бағдарлау 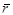параметрлеуге жауапты. Сондай-ақ P,Q,R-D-дағы тегіс функциялар.

Сонда мына формула дұрыс:

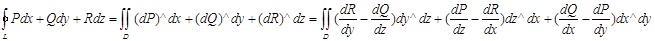
Беттік интегралдың сызықтылығына байланысты 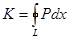интегралы жағдайын қарастыру жеткілікті, яғни 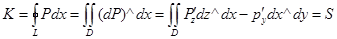формуласын дәлелдейік.

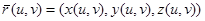- Д бетін параметрлеуі болсын. Әрі 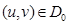. Бұдан басқа, 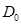облысының шекарасында бөліктік-тегіс параметрлеуі 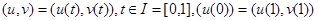, берілген 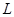қисығындағы 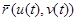параметрлеуін анықтайды. Қисықсызықты интегралдың өрнегі туралы теоремаға байланысты анықталған интеграл арқылы мынаны аламыз: 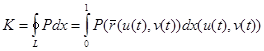. Сол теорема бойынша соңғы интеграл мынаған тең: 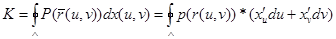Грин формуласын К интегралға қолданамыз. Осы үшін бірінші дифференциалдың инварианттылық формаларын және 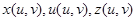функциясының екінші дербес туындысын қолданамыз. Мынаны аламыз: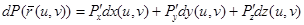

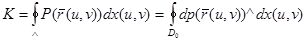Олай болса ,

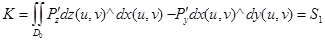
Мұнда 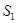жазық 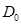облысының жоғарғы жағы бойынша , екінші текті беттік интеграл ретінде қарасытырылады. Бірақ 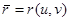параметрлеу кезінде S және 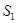екі интеграл да бір және сол өрнекті береді. Осыған көз жеткізу үшін, 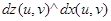және 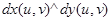өрнегіндегі жақшаны ашу жеткілікті, тек мұнда 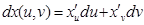деп есептейміз. Түпкілікті мынаны аламыз, яғни S және 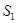бір және сол қос интегралға келтіріледі. 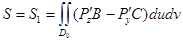мұндағы ,

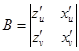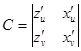
Сонымен K=S теңдігі дәлелденді. Дәлелденді.

Тек интегралдау шектеріне ғана тәуелді қисықсызықты интегралдар

Тіктөртбұрышта шектелген функцияның Риман бойынша интегралдануы

Теорема 1. Шектелген 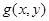функциясы 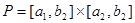-де интегралданған болуы үшін, мына эквивалентті шарттардың біреуінің орындалуы қажетті және жеткілікті:

1)

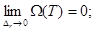
2)

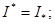
3)

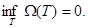
Дәлелдеуі: Алдымен функцияның интегралдану эквиваленттік шартының 1) шартын дәлелдейік.

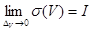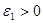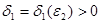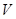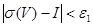Қажеттілігі болсын. Бұл кез келген үшін, мынадай табылып, кез келген үлестірілген бөлінуі үшін шартымен орындалады, яғни (*)

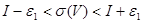Еркін үлестірілген 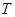бөлінуді 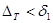шартымен қарастырамыз. Ол үшін мынаны аламыз: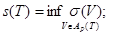 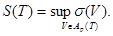Онда (*) теңсіздігінен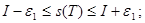 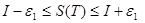шығады. Олай болса 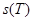және 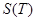мәндері ұзындығы 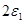бір 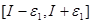кесіндісінде жатады, яғни мына теңсіздік орындалады: .

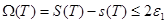Егер 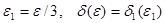деп алсақ, онда мынаны аламыз: кез келген 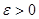үшін мынадай 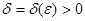саны табылып, әрбір 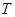бөліну кезінде 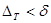шартымен 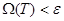орындалады, яғни 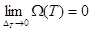қатынасы орынды. Қажеттілігі дәлелденді.

Жеткіліктілігі. 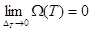шегінінің шартынан 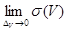шегінің шығатынын дәлелдеу керек.

Алдымен, 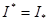екеніне көз жеткізейік. Лемма 6-дан кез келген 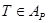бөлінуі үшін, 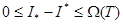аламыз. Олай болса, 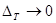кезінде 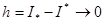. 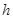тұрақты сан болғандықтан, 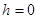және 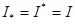. 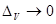кезінде 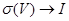дәлелдеу қалды. Еркін түрде оң 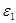санын алайық. 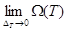шегінің бар болу шартынан мынадай 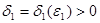санын табуға болады, 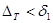шартымен барлық 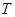бөліну үшін 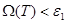теңсіздігі орындалады. Бірақ, онда осы бөлінудің кез келген 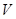белгісі үшін мынаны аламыз:

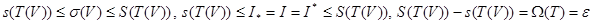, яғни ұзындығы 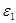-ден аспайтын, екі 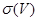және 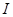нүктелері 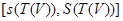кесіндісінде жатады. Бұл осы нүктелерінің арасындағы қашықтықта 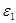-ден аспайды деген сөз, сондықтан , 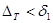кез келген үлестірілген бөліну үшін 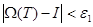болады. Олай болса, 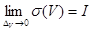дәлелденді.

Сонымен, Теорема 1-дің 1) шарты Риман бойынша функцияның интегралдану шартымен эквивалентті. Енді 1,2 және 3 шарттардың эквиваленттілігін дәлелдейік. Ол үшін мына ұйғарымдар тізбелерінің дұрыстығына көз жеткізейік: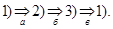

а) Егер 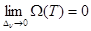болса, онда 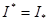екенін дәлелдеу керек. Бірақ бұл 1) шарттың жеткіліктілігін дәлелдеу кезінде тағайындалған.

б) Алдымен, 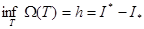болатынын дәлелдейік. 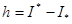саны 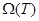-ның төменгі жағы ендеше Лемма 6-дан 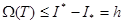аламыз. 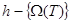жиынының нақты төмен жағы екенін дәлелдейік. Ол үшін еркін 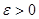санын аламыз. Сонда Дарбу қосындысының анықтамасынан мынадай 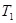және 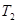бөлінулері табылып, 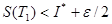; 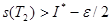аламыз. 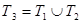бөлінуін аламыз. Сонда, 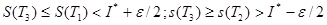; Бұдан 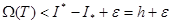шығады, яғни 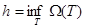. Олай болса, дәлелденгеннен және 2) шарттан 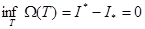аламыз. Сонымен, б) ұйғарымы дәлелденді.

в) Егер 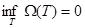болса, онда 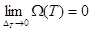болатынын дәлелдеу керек. Кез келген 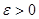үшін , мынадай 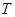бөліну табылып, 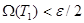. 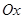және 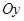өстері бойынша 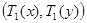бөлінулерінің жұбы 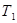бөлінуге сәйкес 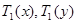бөлінулерінің нүктелер санын 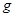арқылы белгілейміз. Сонан,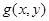 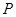-да шектелген болғандықтан мынадай 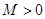табылып, барлық 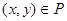үшін, 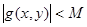. Тіктөртбұрыш 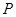-ның ең үлкен қабырғасының ұзындығын 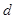арқылы белгілейміз. Енді 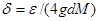-ді қоямыз. 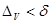шартымен кез келген 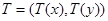бөлінуін аламыз. Сонда 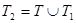бөлінуі үшін, 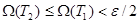болады, өйткені 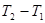бөлінуінің ұсақталуы , яғни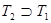 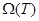шамасын жоғарыдан бағалауға көшеміз. 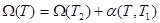мұндағы 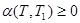, өйткені 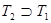. Сонымен бірге 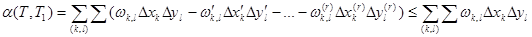, мұндағы

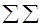символы қосынды 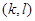жұбы бойынша жүргізілетінін білдіреді. 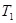бөліну (немесе 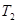) 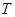бөлінудің 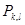тіктөртбұрышы 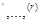индекстерімен кішірек тіктөртбұрыштарға жіктеледі. Басқаша айтқанда, мынадай 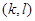жұбының 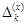немесе 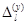кесіндісінің ішінде кем дегенде бір 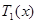немесе 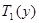бөлінуінің нүктесі жатады.