Основы электромагнитной теории света

Введение.

Оптика является одним из наиболее интересных и плодотворных разделов физики, оказавшей огромное влияние не только на развитие других наук, но и во многом определившей современное научное мировоззрение. История оптики уходит к древнейшим временам и в древнеегипетских и античных документах можно найти упоминания о лупах и очках, изготовленных из драгоценных камней, а также попыток выяснить природу света и объяснить некоторые оптические явления, в частности законы преломления и отражения. ( Евклид, Птолемей, Аристотель и др.) Но наиболее важным результатом той древней оптики является то, что она способствовала появлению геометрии, науки, которой мы успешно пользуемся до настоящего времени. Это во многом объясняется тем, что основное понятие геометрии - прямая линия - ассоциируется с лучом света.

В средние века были изобретены основные оптические приборы - зрительные трубы и микроскопы. Совершенно ясно, что именно они позволили понять строение вселенной и управляющих ею законы механики (Галилей, Кеплер), а также заглянуть в мир микроорганизмов ( Левенгук ).

Несколько позже появились теории, объясняющие природу света: Ньютона - полагавшего, что свет это поток частиц - корпускул, двигающихся по прямым линиям - лучам, и Гюйгенса - считавшего, что свет это волновой процесс. Эти теории приводили к одинаковым результатам, но долгое время они конфликтовали между собой из-за принципиальных разногласий. Однако большее предпочтение отдавалось корпускулярной, во многом благодаря огромному авторитету Ньютона. Лишь спустя более 100 лет Френелю удалось теоретически и экспериментально показать справедливость волнового представления света. Непротиворечивость этих подходов к природе света была доказана лишь после появления системы уравнений Максвелла, показывающих, что электромагнитные поля распространяются в виде волн, а вся теория Френеля может быть получена как следствие этих уравнений. Вскоре трудами Гамильтона, Шварцшильда и других было показано, что корпускулярная теория как анализ систем уравнений хода лучей, которые могут быть интерпретированы как траектории корпускул, может быть построена на решениях уравнения эйконала, получаемого из уравнений Максвелла предельным переходом 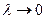. При этом физическое наличие же самих световых частиц - корпускул не предполагалось. Таким образом, произошло примирение подходов к оптике Ньютона и Гюйгенса.

На рубеже XIX и XX веков в физике произошла настоящая революция: наука столкнулась с явлениями, которые, разработанные к тому времени теории не могли объяснить. Это были вопросы, связанные с излучением черного тела и постоянства скорости света относительно систем, движущихся с разными скоростями. Как известно, первое из этих затруднений было преодолено благодаря квантовой теории, в основе которой было предположение (вскоре экспериментально подтвержденное), что все материальные тела имеют волновые свойства (т.н. волны де Бройля) и их влияние усиливается с уменьшением длины волны, которая, в свою очередь, обратно пропорциональна энергии и импульсу этого тела. Де Бройль выдвинул эту гипотезу по аналогии связи лучевой ( корпускулярной ) и волновой теорией распространения света. В квантовой механике это положение так и называется - оптико-механические аналогии.

Второй, упомянутый выше эффект, был обнаружен с помощью оптического прибора - интерферометра Майкельсона и положил начало другой, не менее впечатляющей и плодотворной теории - теории относительности. Одним из ее выводов является, что электромагнитное поле обладают массой и импульсом, т.е. в какой-то мере подобно материальному телу и его можно считать потоком элементарных частиц - фотонов. Их наличие было также экспериментально обнаружено. Таким образом, спустя много лет, подтвердилась и гипотеза Ньютона о корпускулярной теории света, уже как о потоке частиц фотонов - корпускул. В настоящее время никаких противоречий между волновым и фотонным подходам к оптике нет, они описывают разные свойства одного явления, и это обстоятельство называется дуализмом света.

В настоящее время оптика продолжает бурно развиваться. Изобретение лазеров в середине ХХ века привела к появлению таких новых направлений, как голография, оптическая связь, лазерные технологии, интегральная оптика и многие другие; прогресс в оптическом производстве и внедрение вычислительной техники позволило создать как высококачественные оптические приборы для массового спроса, так и уникальные, в частности сверхмощные телескопы; оптические приборы для измерения и контроля подняли уровень автоматизации производства практически во всех отраслях на небывало высокую уровень - все это свидетельствует о той важной роли, которую играет оптика в нынешнюю эпоху научно - технической революции.

Надо полагать, что и в дальнейшем оптика будет занимать достойное место в науке и технике. Конечно, трудно заглядывать в будущее, но одно несомненное качество оптических систем - их колоссальное информационное пропускание, наверняка будет востребовано.

Основы электромагнитной теории света

В настоящем курсе будет рассматриваться лишь волновая теория света. Представление света потоком фотонов изучается в других дисциплинах. Это касается, в основном, взаимодействия света с веществом, здесь мы этих вопросов касаться не будем.

Уравнения Максвелла

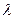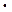Диапазоном световых колебаний или оптическим диапазоном считается интервал длин волн электромагнитных колебаний от =0,01 10 ^-3 мм до 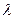=10 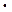10 ^-3 мм. При этом интервал от 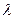=0,38 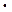10 ^-3 мм до 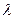=0.76 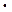10^{- 3 мм называется видимым диапазоном, так как свет только из этого промежутка длин волн воспринимается человеческим глазом. Оптическое излучение, с длинами волн, больших, чем у видимого интервала, называется инфракрасным, а меньшим - ультрафиолетовым излучением.}

Из курса физики известно, что все электромагнитные явления, соответственно электромагнитные волны оптического диапазона, подчиняются системе уравнений Максвелла, которые в интегральной и дифференциальной форме имеют вид

.

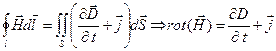(1,1)

закон Био и Саварра.

;

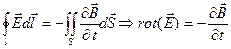(1.2)

закон электромагнитной индукции.

;

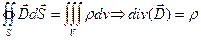(1.3)

закон Гаусса.

;

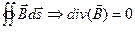(1.4)

отсутствие магнитных зарядов ( невозможность разделить полюса магнита )

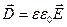;	(1.5)
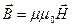,	(1.6)

так называемые материальные уравнения, где 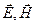- векторы напряженности электрического и магнитного поля, соответственно; 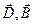- векторы электрической и магнитной индукции, соответственно; 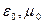- диэлектрическая и магнитная проницаемости вакуума, соответственно. 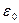=8,8542 10^-12 ф/м, 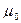=1,256637 10^-6 гн/м, 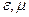- диэлектрическая и магнитная проницаемости среды, соответственно; 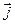- плотность тока; 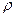-объемная плотность зарядов.

Здесь необходимо отметить, что выражения (1.5) и (1.6) предполагают, что векторы напряженностей электрического и магнитного полей 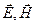коллинеарны соответствующим индукциям, поэтому считается, что 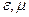скаляры. Это справедливо лишь для изотропных сред, для анизотропных же это условие не выполняется. В этом случае для однородных, но анизотропных сред 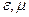являются постоянными тензорами, т.е. имеют вид матриц.

Будем предполагать, что свет распространяется в однородных диэлектрических средах ( 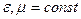и скаляры) в которых отсутствуют заряды ( 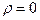) и не должно быть токов ( 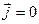). Получим из этой системы волновое уравнение. Для этого применим к обеим частям уравнения (1,1) операцию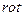

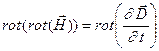. (1.7)

Воспользовавшись известной формулой векторного анализа

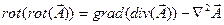, (1.8)

где 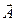- произвольный вектор, а 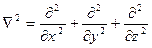- оператор Лапласа. Меняя порядок дифференцирования в правой части (по времени и координатам), а, также учитывая, что 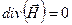, так как из (1,6) 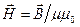в силу (1.3) получим

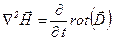. (1.9)

Учитывая, что 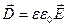и воспользовавшись уравнением (1.2), где в правой части с помощью (1.6) , 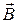надо выразить через 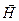, окончательно получим

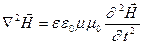. (1.10)

Данное выражение представляет волновое уравнение и его решение описывает бегущую волну. Покажем это.

Для простоты рассмотрим одномерный случай, когда электромагнитное поле изменяется лишь вдоль оси 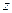(общий случай получится по аналогии). Тогда 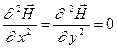и волновое уравнение примет вид

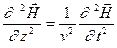, (1.11)

где .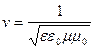

Уравнение Гельмгольца

Следует напомнить, что 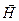- вектор, состоящий из трех компонент

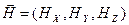, (2.1)

и уравнение (1.11) представляет собой систему из трех аналогичных уравнений для каждой такой компоненты, т.е. каждое уравнение будет иметь такой же вид как (1.11), но вместо 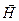, надо писать 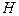с индексом, соответствующий данной компоненте. Для определенности выберем 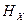. Т.е. уравнение будет выглядеть как

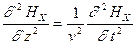. (2.2)

В курсах математики доказывается, что решение такого типа уравнения выглядит следующим образом

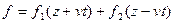, (2.3)

где 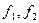- произвольные функции, . Проанализируем полученное выражение.

Решение состоит из двух слагаемых. Рассмотрим каждое из них. Удобнее начать со второго. В силу однозначности функции 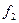из условия 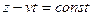следует, что 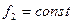, т.е. положение 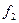однозначно зависит от времени, при этом вид функции 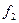не меняется. Другими словами, если 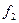в момент времени 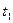она находилась в точке с координатой 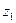, то в момент времени 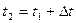, эта функция, без всяких деформаций будет находиться в точке с координатой 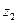, которую можно определить из следующего соотношения

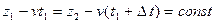. (2.4)

Откуда смещение

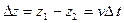. (2.5)

Таким образом, за время 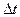функция 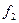(в нашем случае компонента магнитного поля) двигалась с постоянной скоростью 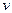в направлении оси 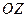. Первое слагаемое описывает аналогичный процесс, только поле в этом случае движется в противоположную сторону. Таким образом, решение этого уравнения, в общем случае, описывает движения двух, вообще говоря, разных компонентов 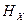(а это и есть электромагнитные волны) в двух противоположных направлениях.

Таким образом, 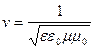является скоростью распространения электромагнитных волн. В вакууме 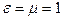; подставляя сюда значения 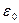и 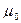из (1.6), найдем, что скорость электромагнитных волн в вакууме или скорость света равна (ее принято обозначать буквой ).

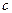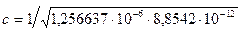=2,9979 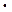10⁸ [м/сек], (2.6)

т.к. [генри 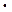фарада] = [сек²].

Из выражения для 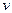следует, что если электромагнитные волны распространяются в среде, где 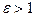и 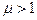, их скорость уменьшается, т.к. .

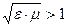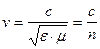, (2.7)

где 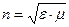. Величина 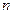, показывающая, во сколько раз скорость света в среде меньше скорости света в вакууме называется показателем преломления этой среды. Это параметр характеризует среду и, поэтому, он играет очень большую роль в оптике.

Общее решение уравнения в частных производных определяются с точностью до произвольных функций. Конкретное решение получается после задания начальных и граничных условий, т.е. если 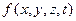- решение волнового уравнения, то

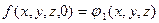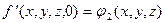; - начальные условия , (2.7а)

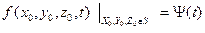-граничное условие, (2.7б)

Граничные условия в волновых процессах в подавляющем большинстве случаев представляют собой периодические функции времени и их можно представить в виде рядов Фурье.

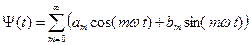. (2.8)

Если ограничиться рассмотрением установившихся процессов, т.е. пренебречь переходными процессами (в оптическом диапазоне это вполне оправдано), то решение будет иметь вид

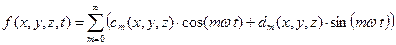, (2,9)

где 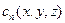и 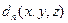пока неизвестные функции, представляющие собой амплитуды. После подстановки (2.9) в волновое уравнение и приравнивания выражений у одинаковых гармоник, для каждой амплитуды мы получим уравнение в частных производных, не содержащее .

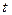Очень удобно представлять периодические процессы в комплексной форме, используя формулу Эйлера

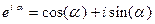. (2.10)

Тогда выражение (2.9) будет выглядеть следующим образом

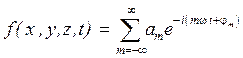, (2.11)

где 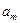- амплитуда, 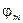- фаза. При такой записи, все промежуточные преобразования проводятся значительно проще, а обратный переход к тригонометрической форме записи осуществляется при помощи операции взятия действительной части комплексного выражения, правда все преобразования должны быть линейными.

Будем решать волновое уравнение (1.10) для одной из компонент 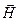(для определенности 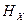) в предположении, что граничное условие представляет собой одночастотную периодическую функцию времени (для оптического диапазона это условие имеет физический смысл, об этом позже). Т.е. будем искать решение в виде

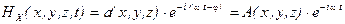, (2.12)

где 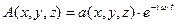- т.н. комплексная амплитуда. После подстановки (2.12) (1.10) и упрощений получим

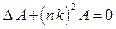, (2.13)

т.к. 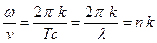, где 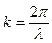- параметр, называемый волновым числом. Полученное выражение называется уравнением Гельмгольца, оно проще волнового тем, что не имеет зависимости от времени.