Справочный материал к выполнению ргз

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО РЫБОЛОВСТВУ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

“МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ”

Кафедра высшей математики

и программного обеспечения ЭВМ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ,

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И

СЛУЧАЙНЫЕ ПРОЦЕССЫ

Методические рекомендации к выполнению РГЗ

для студентов 2 курса

по дисциплине «Математика»

Мурманск

Составитель: Казакова Галина Борисовна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Методические рекомендации рассмотрены и одобрены кафедрой 2 апреля 2008 г., протокол № 6

Рецензент: Кацуба В.С., канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ.. 4

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РГЗ. 4

СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА.. 13

И ССЫЛКИ НА ЛИТЕРАТУРУ.. 13

СПРАВОЧНЫЙ МАТЕРИАЛ К ВЫПОЛНЕНИЮ РГЗ. 14

1. Случайные величины.. 14

1.1. Случайные величины.. 14

1.2 Дискретная случайная величина и ее числовые характеристики. 15

1.3. Непрерывная случайная величина и ее числовые характеристики. 16

1.4. Нормальное распределение. 16

2. Математическая статистика.. 17

2.1. Генеральная и выборочная совокупности. 17

2.2. Вариационные ряды.. 18

2.3. Числовые характеристики. 19

2.4. Точечные оценки. 21

2.5. Интервальные оценки. 22

2.6. Проверка статистических гипотез. 25

2.7. Основные понятия корреляционного и регрессионного анализов. 27

2.8. Парная регрессия. 28

2.9. Выборочный коэффициент корреляции. 29

3. Случайные процессы.. 31

РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА РГЗ. 32

СПИСОК ЛИТЕРАТУРЫ... 46

ВВЕДЕНИЕ

Настоящее пособие предназначено для студентов и курсантов 2 курса, обучающихся по техническим специальностям. В пособии содержатся методические рекомендации к изучению теоретического материала и выполнению РГЗ по теме "Теория вероятностей, математическая статистика и случайные процессы", варианты РГЗ и список рекомендуемой литературы.

В результате изучения этой темы студенты(курсанты) должны:

· знать основные положения теории вероятностей; основные положения математической статистики; основы теории случайных процессов;

· уметь применять методы теории вероятностей, математической статистики и теории случайных процессов для решения практических задач.

Данные методические рекомендации включают краткий справочный материал для выполнения контрольной работы, который нужно рассматривать как дополнение к имеющимся учебникам по теории вероятностей и математической статистике. Так же в пособии содержится подробное решение примерного варианта контрольной работы со ссылками на используемый справочный материал.

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РГЗ

Перед выполнением РГЗ необходимо ознакомится сначала со справочным материалом, затем более глубоко изучить теоретический материал и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу.

Задача 1.

В каждом варианте для заданной случайной величины 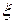составить закон распределения, построить многоугольник распределения вероятностей, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

Вариант 1. Вероятность отказа каждого прибора при проведении испытания равна 0,4, для испытания было отобрано 4 прибора, случайная величина 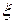– число приборов, отказавших при проведении испытаний.

Вариант 2. Вероятность совершить покупку для каждого покупателя магазина равна 0,3, в магазин пришли 4 покупателя, случайная величина 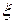– число покупателей, совершивших покупку.

Вариант 3. По многолетним статистическим данным известно, что вероятность рождения мальчика равна 0,515, случайная величина 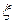– число мальчиков в семье из 4 детей.

Вариант 4. Вероятность того, что корреспондент примет вызов радиста, равна 0,4, случайная величина 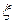– число вызовов, принятых корреспондентом, если радистом было передано 4 вызова.

Вариант 5. В рекламных целях торговая фирма вкладывает в единицу товара денежный приз размером 1 тыс. руб., случайная величина 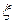– размер выигрыша при четырех сделанных покупках, если вероятность выигрыша в каждой покупке равна 0,1.

Вариант 6. В контрольной работе 4 задачи, вероятность правильного решения учеником каждой задачи 0,7, случайная величина 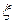– число правильно решенных задач.

Вариант 7. Торговый агент имеет четырех потенциальных покупателей, вероятность того, что потенциальный покупатель сделает заказ, равна 0,4, случайная величина 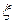– число покупателей, сделавших заказ.

Вариант 8. Студент должен сдать в сессию 4 экзамена, вероятность успешной сдачи каждого экзамена 0,7, случайная величина 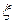– число экзаменов, которые сдал студент в сессию.

Вариант 9. Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0,2. В случайном порядке выбраны четыре телезрителя, случайная величина 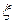– число лиц, видевших рекламу.

Вариант 10. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна 0,75, контроль расхода электроэнергии производится в течение четырех суток, случайная величина 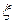– число дней, в которые расход электроэнергии был выше установленной нормы.

Задача 2

Вариант 1. Значения теста IQ (коэффициента интеллекта) Стэнфорда – Бине распределены приблизительно по нормальному закону с математическим ожиданием 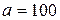и средним квадратическим отклонением 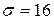. Найти вероятность того, что коэффициент интеллекта у случайно отобранного для тестирования человека окажется меньше 95.

Вариант 2. Заряд охотничьего пороха отвешивается на весах. Вес заряда - нормально распределенная случайная величина c параметрами а = 2,3 г и 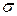=150 мг. Найти вероятность повреждения ружья при выстреле, если максимально допустимый вес заряда пороха равен 2,5 г.

Вариант 3. Размер детали подчинен нормальному закону с параметрами 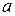= 30 см и 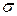= 5 см. Детали считаются годными, если их размер находится в пределах от 20 до 40 см. Если размер детали больше 40 см, то она подлежит переделке. Найти вероятность того, что случайно отобранная деталь подлежит переделке.

Вариант 4. Значения теста IQ (коэффициента интеллекта) Стэнфорда – Бине распределены приблизительно по нормальному закону с математическим ожиданием 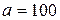и средним квадратичным отклонением 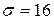. Найти вероятность того, что коэффициент интеллекта у случайно отобранного для тестирования человека окажется в пределах от 80 до 120.

Вариант 5. Средняя длина взрослой рыбы оценивается в 65 см. со стандартным отклонением в 5 см. Считая распределение длины рыбы нормальным, найдите вероятность того, что длина конкретной рыбы будет больше 70 см.

Вариант 6. Спортсмен бросает копье. Дальность полета копья – нормально распределенная случайная величина со средним значением 70 м и средним квадратическим отклонением 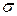=5 м. Найти вероятность того, что дальность полета копья будет от 65 до 72 м.

Вариант 7. На рынок поступила крупная партия говядины. Предполагается, что вес туш – случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием 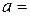950 кг и средним квадратическим отклонением 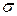=150 кг. Определить вероятность того, что вес случайно отобранной туши будет между 800 и 1300 кг.

Вариант 8. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед. Найти вероятность того, что цена акции будет не выше 15,3 ден. ед.

Вариант 9. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед. Найти вероятность того, что цена акции будет в интервале от 14,9 до 15,3 ден. ед.

Вариант 10. На рынок поступила крупная партия говядины. Предполагается, что вес туш – случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием 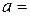950 кг и средним квадратическим отклонением 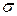=150 кг. Найти вероятность того, что вес случайно отобранной туши окажется больше 1250 кг.

Задача 3.

Из генеральной совокупности, распределенной по нормальному закону, сделана выборка. Найти: 1) числовые характеристики выборки – выборочную среднюю, выборочную дисперсия, выборочное среднее квадратическое отклонение; 2) несмещенные оценки для генеральной средней и генеральной дисперсии; 3) доверительный интервал для оценки генеральной средней с заданной надежностью γ.

Вариант 1.

	54-58	58-62	62-66	66-70	70-74	74-78	78-82

.

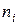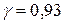Вариант 2

	154-158	158-162	162-166	166-170	170-174	174-178	178-182

.

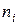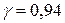Вариант 3.

	0-200	200-300	300-400	400-500	500-600	600-700

.

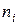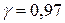Вариант 4.

	33,2	38,2	43,2	48,2	53,2

.

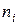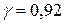Вариант 5.

	15,4	18,4	21,4	24,4	27,4

.

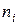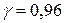Вариант 6.

.

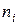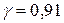Вариант 7.

	4 - 9	9 - 14	14 - 19	19 - 24	24 - 29

.

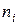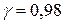Вариант 8.

	12,4	16,4	20,4	24,4	28,4	32,4	36,4

.

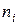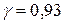Вариант 9.

	1,7– 2,8	2,8– 3,9	3,9-5,0	5,0-6,1	6,1-7,2	7,2-8,3

.

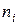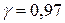Вариант 10.

	3 - 7	7 - 11	11- 15	15 - 19	19 - 23

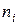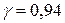
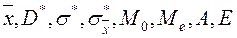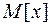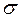Задача 4. Систематизировать выборку из n вариант по разрядам и выполнить её статическую обработку по способу моментов, вычислив и доверительные интервалы для и при g=0,95, а также построить полигон частостей, гистограмму и кумуляту.

Нагрузки x (кВт) на вспомогательный двигатель БМРТ «Алтай» во время промысла в районе Баренцева моря в течение n часов характеризуется выборкой объёма n, извлечённой из машинного электротехнического журнала.

Вариант 1.

850, 860, 900, 920, 650, 640, 620, 600, 600, 600, 580, 560, 550, 640, 640, 650, 670, 700, 700, 700, 720, 740, 750, 760, 780, 800, 800, 840, 840, 550, 550, 540, 540, 520, 500, 500, 500, 480, 460, 460, 460, 460, 450, 440, 440, 400, 400, 380, 350, 300.

Вариант 2.

600, 610, 620, 630, 640, 650, 650, 670, 670, 670, 690, 690, 700, 720, 730, 750, 750, 790, 790, 790, 800, 820, 840, 850, 850, 856, 500, 480, 450, 450, 430, 420, 420, 420, 310, 350, 350, 380, 380, 380, 500, 510, 520, 550, 550, 550, 550, 580, 580, 590.

Вариант 3.

510, 520, 530, 550, 550, 550, 550, 560, 570, 590, 600, 600, 630, 640, 650, 650, 650, 650, 650, 650, 650, 660, 680, 690, 500, 480, 470, 450, 450, 450, 450, 440, 430, 700, 710, 720, 750, 750, 780, 800, 850, 850, 800, 400, 390, 380, 350, 350, 350,340.

Вариант 4.

420, 430, 450, 450, 450, 450, 450, 480, 480, 490, 490, 500, 500, 620, 610, 620, 640, 650, 650, 650, 680, 690, 700, 600, 580, 570, 560, 560, 550, 550, 550, 550, 540, 520, 550, 550, 520, 520, 510, 500, 500, 390, 380, 370, 350, 350, 330, 300, 250, 240.

Вариант 5

510, 510, 520, 520, 530, 540, 550, 550, 550, 550, 550, 560, 560, 580, 590, 600, 610, 640, 650, 670, 500, 480, 470, 460, 450, 450, 450, 450, 450, 440, 430, 420, 410, 410, 400, 390, 380, 350, 350, 350, 340, 330, 320, 310, 300, 290, 280, 250, 250,230.

Вариант 6

460, 470, 480, 500, 520, 540, 650, 670, 700, 700, 720, 650, 640, 630, 600, 600, 600, 600, 600, 600, 600, 580, 560, 560, 570, 570, 540, 540, 500, 350, 340, 300, 290, 360, 380, 400, 400, 410, 440.

Вариант 7.

560, 570, 580, 590, 600, 600, 600, 600, 600, 600, 610, 620, 630, 640, 650, 660, 680, 700, 700, 740, 360, 370, 380, 400, 400, 400, 410, 430, 440, 440, 460, 470, 470, 480, 480, 490, 490, 500, 500, 500, 500, 520, 510, 540, 300, 300, 290, 270, 310, 320.

Вариант 8.

360, 370, 380, 400, 400, 400, 400, 420, 420, 440, 650, 650, 670, 680, 690, 690, 700, 700, 700, 710, 760, 640, 640, 630, 630, 620, 600, 600, 600, 600, 600, 590, 580, 580, 570, 570, 540, 540, 530, 520, 510, 500, 500, 500, 500, 500, 490, 470, 460, 450.

Вариант 9.

460, 470, 480, 490, 500, 500, 500, 500, 500, 500, 510, 520, 530, 540, 550, 400, 400, 400, 400, 420, 440, 390, 380, 370, 360, 340, 330, 300, 300, 290, 280, 660, 670, 690, 700, 700, 700, 710, 730, 740, 652, 640, 630, 600, 600, 600, 590, 580, 570, 560.

Вариант 10.

500, 500, 500, 500, 510, 530, 550, 490, 490, 480, 470, 460, 460, 470, 470, 460, 450, 440, 440, 430, 420, 410, 410, 410, 400, 400, 400, 390, 380, 360, 360, 380, 400, 300, 320, 610, 620, 600, 600, 600, 700, 720, 640, 630, 590, 580, 570, 560, 570, 600.

Вариант 11.

410, 420, 430, 440, 450, 450, 450, 450, 450, 450, 460, 470, 480, 480, 490, 500, 490, 510, 520, 530, 540, 550, 550, 560, 570, 580, 580, 310, 320, 330, 340, 350, 350, 350, 350, 370, 360, 310, 320, 310, 250, 240, 700, 750, 690, 680, 670, 650, 650, 630.

Вариант 12.

520, 520, 530, 540, 550, 550, 550, 550, 550, 550, 570, 580, 590, 510, 510, 490, 490, 480, 470, 460, 450, 450, 450, 450, 440, 430, 420, 610, 620, 640, 650, 650, 660, 660, 670, 680, 690, 710, 750, 390, 380, 370, 350, 350, 350, 350, 340, 330, 290, 250.

Задача5 .

Имеются две нормально распределенные генеральные совокупност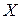и и 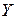, из которых были сделаны выборки. По полученным выборкам на уровне значимости 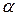проверить гипотезу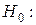 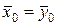, считая дисперсии неизвестными, но равными.

Вариант 1.

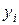Уровень значимости 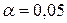, альтернативная гипотеза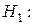

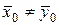
Вариант 2.

Уровень значимости 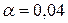, альтернативная гипотеза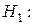

Вариант 3.

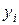Уровень значимости 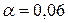, альтернативная гипотеза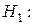

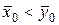
Вариант 4.

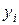Уровень значимости 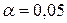, альтернативная гипотеза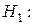

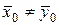
Вариант 5.

Уровень значимости 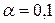, альтернативная гипотеза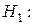

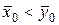
Вариант 6.

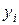Уровень значимости 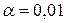, альтернативная гипотеза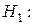

Вариант 7.

Уровень значимости 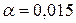, альтернативная гипотеза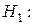

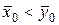
Вариант 8.

Уровень значимости 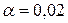, альтернативная гипотеза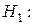

Вариант 9.

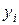Уровень значимости 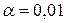, альтернативная гипотеза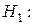

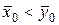
Вариант 10.

Уровень значимости 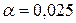, альтернативная гипотеза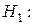

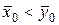
Задача 5.

Была исследована зависимость признака 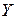от признака 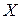. В результате проведения 10 измерений были получены результаты, представленные в таблице.

Требуется: 1) оценить тесноту и направление связи между признаками с помощью коэффициента корреляции и оценить значимость коэффициента корреляции на уровне значимости 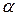; 2) найти уравнение линейной регрессии 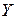на 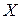; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.

Вариант 1.

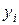Уровень значимости .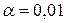

Вариант 2.

	6,0	6,5	6,8	7,0	7,4	8,0	8,2	8,7	9,0	10,0

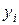Уровень значимости .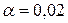

Вариант 3.

	39,0	38,7	38,9	40,1	39,4	39,4	39,5	39,1	40,4	39,5

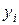Уровень значимости .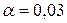

Вариант 4.

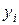Уровень значимости .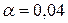

Вариант 5.

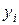Уровень значимости .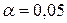

Вариант 6.

	3,5	4,0	3,8	4,6	3,9	3,0	3,5	3,9	4,5	4,1
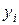	4,2	3,9	3,8	4,5	4,2	3,4	3,8	3,9	4,6	3,0

Уровень значимости .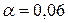

Вариант 7.

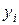				2,5	3,5

Уровень значимости .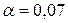

Вариант 8.

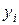Уровень значимости .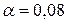

Вариант 9.

	2,8	2,2	3,0	3,5	3,2	3,7	4,0	4,8	6,0	5,4
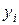	6,7	6,9	7,2	7,3	8,4	8,8	9,1	9,8	10,6	10,7

Уровень значимости .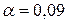

Вариант 10.

	3,2	3,7	4,0	4,8	6,0	5,4	5,2	5,4	6,0	9,0
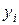	8,4	8,8	9,1	9,8	10,6	10,7	11,1	11,8	12,1	12,4

Уровень значимости .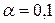

Задача 6.

Задан процесс Пуассона 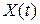с интенсивностью 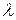. Найти вероятность того, что за время 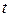событие 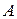произойдет: 1) ровно 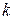раз; 2) меньше, чем 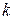раз; 3) не больше, чем 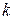раз.

№ варианта		№ варианта

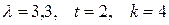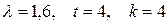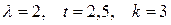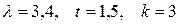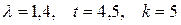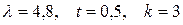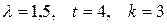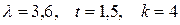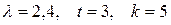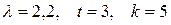СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

И ССЫЛКИ НА ЛИТЕРАТУРУ

№ темы	Содержание	Литература
	Дискретные случайные величины, их числовые характеристики и законы распределения	[1], гл. 3, § 3.1, 3.3, 3.4, 3.8; [2], гл. 2, § 2.1, 2.2, 2.5; [3], Ч. 2, гл. 6, § 1, 2, 3; гл. 7, § 1, 2; гл. 8, § 2–4, 7; [4], Ч. 2, гл. 4, § 1, № 165, 166, 171, 173; § 3, № 188, 211, 219; [5], гл. V, § 5, 860–867, § 6, № 873, 874
	Непрерывные случайные величины. Нормальный закон распределения	[1], гл. 3, § 3.6; гл. 4, § 4.7; [2], гл. 2, 2.4, 2.5, 2.7; [3], Ч. 2, гл. 12, § 1–3, 5; [4], Ч. 2, гл. 9, № 322, 328, 329, 332, 335; [5], гл. V, § 11, № 904–916
	Выборки и их числовые характеристики. Статистические оценки неизвестных параметров генеральной совокупности	[1], гл. 8, § 8.1, 8.2; гл. 9, § 9.1, 9.2, 9.4, 9.6, 9.7; [2], гл. 6, 6.1–6.5; гл. 7, § 7.1, 7.3, 7.4; [3], Ч. 3, гл. 15, § 1, 3, 6; гл. 16, §1, 3, 4, 8–10, 13–16; [4], Ч. 3, гл. 10, § 1, № 450, 454–457, 459, 461, 466; [5], гл. V, § 17, № 947, 948, 950, 951, 953
	Проверка статистических гипотез	[1], гл. 10, § 10.1–10.3; [2], гл. 7, § 7.5, 7.6; [3], Ч. 3. гл. 19, § 1, 3–6, § 10; [4], Ч. 3, гл. 13, § 1, § 4, № 568, 569; §5, № 570, 573;
	Элементы корреляционного и регрессионного анализа	[1], гл. 12, § 12.1–12.5; [3], Ч. 3, гл. 18, § 1–4, 7; гл. 19, §22; [4], Ч. 3, гл. 12, § 1; гл. 13, § 12, №611, 612; [5], гл. V, § 16, № 943–945
	Случайные процессы. Процесс Пуассона (простейший поток событий)	[1], гл. 7, § 7.1, 7.4; [2], гл. 1, § 1.21; [3], Ч. 2, гл. 6, § 6; [4], Ч. 2, гл. 4, § 2;

Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.

СПРАВОЧНЫЙ МАТЕРИАЛ К ВЫПОЛНЕНИЮ РГЗ

Случайные величины

Случайные величины

Случайной величиной 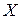называется числовая функция, определенная на пространстве элементарных исходов 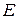, которая каждому элементарному исходу 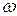ставит в соответствие число .

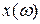Условимся в дальнейшем, как правило, случайные величины обозначать буквами: 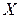, , 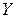…, а принимаемые ими значения – строчными латинскими (с индексами или без): 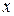, 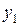и т.д.

Случайные величины делятся на дискретные и непрерывные.

Случайная величина называется дискретной, если значения, которые может принимать данная случайная величина, образуют дискретное (конечное или бесконечное) множество чисел , , …, , …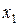

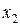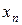Под непрерывной случайной величиной будем понимать величину, значения которой, заполняют конечный или бесконечный промежуток числовой оси .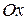

Например, число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.