Лекция №1. Проецирование простых геометрических объектов

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГТУ Московский Институт Стали и Сплавов

Кафедра Инженерной графики

Соломонов К.Н., Чиченева О.Н., Мокрецова Л.О., Головкина В.Б.

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Курс лекций

СОДЕРЖАНИЕ

Раздел 1. Основы образования чертежа. 3

Лекция №1. Проецирование простых геометрических объектов. 3

1.1. Начертательная геометрия, инженерная и компьютерная графика: роль предмета в инженерной деятельности 3

1.2. Методы проецирования. 5

1.3. Комплексный чертеж Монжа. 7

1.4. Графическое отображение точки на комплексном чертеже. 10

1.5. Графическое отображение прямой на комплексном чертеже. 13

1.6. Безосные чертежи. 21

1.7. Взаимное положение прямых. 23

Лекция №2. Плоскость. Позиционные и метрические задачи на плоскости. 26

2.1. Плоскость и ее задание на чертеже. 26

2.2. Плоскости частного и общего положения. 27

2.3. Принадлежность точки и прямой плоскости. 30

2.4. Линии уровня в плоскости. 33

2.5. Взаимное положение прямых и плоскостей. 35

2.6. Графическое решение позиционных и метрических задач. 40

Раздел 2. Поверхности. 48

Лекция №3. Образование поверхностей. Гранные поверхности. 48

3.1. Образование и приближенная классификация поверхностей. 48

3.2. Гранные поверхности. 55

3.3. Принадлежность точки и линии поверхности. 55

3.4. Пересечение гранных поверхностей плоскостями. 62

3.5. Определение натуральной величины фигуры сечения. 64

Лекция №4. Кривые поверхности. Поверхности вращения. 67

4.1. Поверхности вращения. 67

4.2. Принадлежность точки и линии поверхности. 70

4.3. Пересечение поверхностей вращения плоскостями частного положения. 77

4.4. Определение натуральной величины фигуры сечения. 80

Раздел 3. Аксонометрические проекции. 81

Лекция №5. Аксонометрические проекции. 81

5.1. Образование и виды аксонометрических проекций. Коэффициенты искажения. 81

5.2. Прямоугольные изометрическая и диметрическая проекции. 83

5.3. Изображение окружностей на аксонометрических плоскостях. 84

Раздел 4. Пересечение поверхностей. 90

Лекция №6. Пересечение поверхностей, одна из которых занимает частное положение в пространстве. 90

6.1. Алгоритм построения линии пересечения двух поверхностей, 90

6.2. Пересечение гранных поверхностей. 91

6.3. Пересечение гранных поверхностей с поверхностями вращения. 97

Лекция №7. Пересечение поверхностей общего положения. 99

7.1. Взаимное пересечение поверхностей вращения. Метод вспомогательных секущих плоскостей. 99

7.2. Пересечение соосных поверхностей вращения. Метод концентрических сфер. 101

7.3. Теорема Монжа. 105

Раздел 5. Наглядные изображения. Область применения и правила построения. 107

Лекция №8. Единая система конструкторской документации. 107

8.1. Форматы.. 108

8.2. Масштабы.. 110

8.3. Линии чертежа. 110

8.4. Шрифты чертежные. 111

8.5. Нанесение размеров на чертеже. 112

Лекция №9. Виды. Разрезы. Сечения. 114

9.1. Виды.. 114

9.2. Краткая классификация разрезов. 116

9.3. Сечения. 121

9.4. Условности и упрощения. 122

Список использованных источников. 124

Раздел 1. Основы образования чертежа

Лекция №1. Проецирование простых геометрических объектов

1.1. Начертательная геометрия, инженерная и компьютерная графика: роль предмета в инженерной деятельности

Одним из распространенных методов познания природы, законов ее развития, исследования явлений и процессов, происходящих в природе, а также выявления их главных свойств является моделирование, в котором человек создает физическую или абстрактную (математическую) модель процесса или объекта. Физические модели сохраняют природу изучаемого объекта, повторяя его в малых масштабах, а математические модели представляются различного рода уравнениями, которые описывают основные свойства изучаемых процессов.

В инженерной практике мы постоянно встречаемся с геометрическими моделями в виде чертежей, которые и являются средством общения людей в их производственной деятельности.

Математическая наука, занимающаяся изучением графических методов отображения пространства, разработкой научных основ построения и исследования геометрических моделей, проецируемых геометрических объектов (точек, линий, поверхностей) и их отображения на плоскости, называется НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИЕЙ.

Наряду с этим начертательная геометрия развивает пространственное воображение, что позволяет решать графические задачи из других областей знаний.

Основы НГ были обобщены Гаспаром Монжем (1746-1818) — выдающимся французским математиком и инженером, — издавшем в 1799 году книгу под названием «Geometrie descriptive» (начертательная геометрия), базовые понятия которой не претерпели изменений до наших дней.

Название этой дисциплины Г. Монж определил следующим образом:

«Начертательная геометрия преследует две цели. Первая заключается в том, чтобы на чертеже, имеющем лишь два измерения, с точностью изобразить тела трех измерений, лишь бы они были вполне определенными. С этой точки зрения эта геометрия должна быть языком, необходимым как для инженера, составляющего проекты, так и для того, кто по этим проектам должен выполнять работу.

Вторая цель этой науки заключается в способах выводить на основании точного описания тел все свойства, относящиеся к их форме, к их относительному расположению. В этом смысле она является средством изыскания истины и представляет примеры перехода от известного к неизвестному, будучи всегда прилагаема к предметам, подлежащим наибольшей очевидности».

Если, используя высказывание Г. Монжа, считать «чертеж языком техники», то «начертательная геометрия является грамматикой этого языка». Так продолжил мысль Г. Монжа замечательный русский геометр В.И. Курдюмов (1853-1904), развивший в своих трудах ряд положений НГ.

Таким образом, современный инженер должен одинаково свободно владеть как самим языком технического общения (ИНЖЕНЕРНОЙ И КОМПЬЮТЕРНОЙ ГРАФИКОЙ), так и основными правилами, методами и способами построения графических изображений (НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИЕЙ).

Методы проецирования

Правила построения изображений, излагаемые в курсе начертательной геометрии, основаны на методе проекций. Рассмотрение метода проекций начинают с построения проекции точки, на примере которого рассматривают все базовые понятия и правила проецирования.

Это не сужает круг решаемых задач в начертательной геометрии, т.к. все линии и поверхности можно представить как совокупность точек.

Центральное проецирование

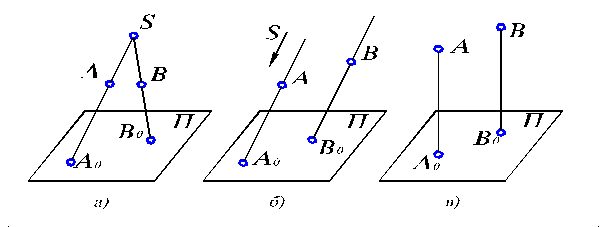
Наиболее общим методом проецирования является центральное проецирование (рис.1.1, а).

Рис. 1.1. Методы проецирования: а) центральное; б) параллельное; в) ортогональное.

Сущность центрального проецирования заключается в следующем: пусть даны плоскость П и точка S (SÏП). Возьмем произвольную точку А (АÏП, АÏS). Через заданную точку S и точку А проводим прямую SА и отмечаем точку А₀, в которой эта прямая пересекает плоскость П. Плоскость П называют плоскостью проекций, точку S центром проецирования, полученную точку А₀ – центральной проекцией точки А на плоскость П, прямую SА – проецирующей прямой. Аналогично можно получить проекцию любой другой точки, например точки В, на том же чертеже. Характерной особенностью получаемых проекций является то, что размеры геометрических объектов будут искаженными. Так, на указанном чертеже видно, что если соединить точки А и В прямой, то ее проекция А₀В₀ значительно больше в размерах, чем прямая АВ.

Наглядным примером центрального проецирования на практике может служить тень на некоторой поверхности (в частности, плоскости) какого-либо предмета, освещенного лампочкой (т.е. точечным источником света).

Параллельное проецирование

Частным случаем центрального проецирования является параллельное (рис. 1.1, б), когда центр проецирования находится в бесконечности. Тогда проецирующие лучи параллельны друг другу. Поскольку в природе трудно представить наглядно такой центр, то образным примером может служить тень, отбрасывыаемая каким-либо предметом, освещенным солнцем. В этом случае солнечные лучи можно считать параллельными друг другу.

Ортогональное проецирование

Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций (рис. 1.1, в), называется ортогональным проецированием.

В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение плоских изображений основано на этом методе.

Из принципов построения ортогональных проекций вытекают основные свойства ортогонального проецирования, которые здесь приведем без доказательства.

Свойства ортогонального проецирования:

v Проекция точки – точка.

v Проекция прямой – прямая.

v Проецирующий луч проецируется в точку.

v Точка принадлежит прямой линии, если одноименные проекции точки принадлежат одноименным проекциям прямой линии.

v Прямые в пространстве параллельны, если их одноименные проекции параллельны.

v Прямой угол проецируется в прямой, если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна к ней (Теорема о прямом угле).

v Прямая линия параллельна плоскости, если она параллельна любой прямой, принадлежащей заданной плоскости.

v Проекция плоской фигуры – плоская фигура.

v Решение задач начертательной геометрии и все дальнейшие построения основываются именно на этих свойствах.

Комплексный чертеж Монжа

Проекция геометрического объекта на одну плоскость, рассмотренная нами ранее, не дает полного и однозначного представления о форме геометрического объекта. Поэтому рассмотрим проецирование хотя бы на две взаимно перпендикулярные плоскости (рис. 1.2), одна из которых расположена горизонтально, а другая вертикально.

Несмотря на наглядность, с чертежом, изображенным на рис 1.2, а работать неудобно, т.к. горизонтальная плоскость на нем показана с искажением. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость развернуть вокруг оси ОХ на 90° и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя вверх. Этот метод предложил Г. Монж.

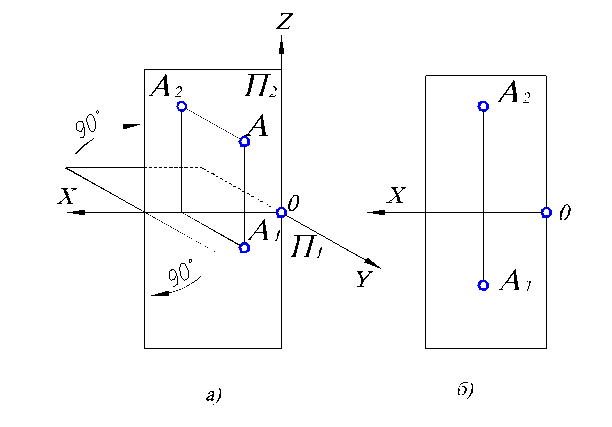
Рис. 1.2. Построение эпюра Монжа:

а) пространственная картина расположения проекций точки А; б) плоскостная картина расположения проекций точки А.

Поэтому чертеж, полученный таким образом (рис. 1.2, б), называется эпюром Монжа или комплексным чертежом.

Обычно двух проекций недостаточно, чтобы составить полное представление о рассматриваемом геометрическом объекте. Поэтому предлагается ввести третью плоскость проекций, ортогональную первым двум (рис.1. 3, а).

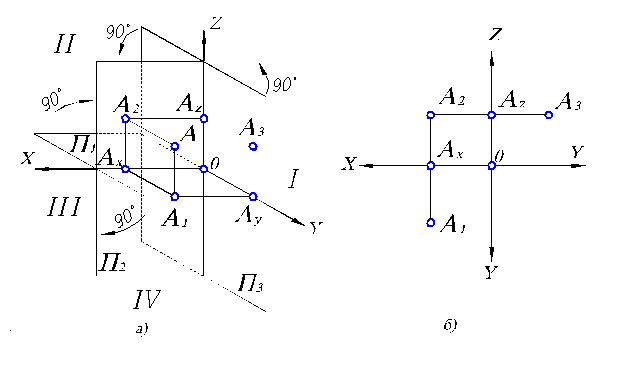
Рис. 1.3. Построение трехкартинного комплексного чертежа (эпюра Монжа):

а) пространственная модель плоскостей проекций; б) трехкартинный комплексный чертеж.

Тогда плоскость П₁ называется горизонтальной плоскостью проекций, П₂ — фронтальной плоскостью проекций (т.к. она расположена перед нами по фронту), П₃ — профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю). Соответственно А₁ — горизонтальная проекция точки А, А₂ — фронтальная проекция точки А, А₃ — профильная проекция точки А.

Оси ОХ, ОY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево. Теперь, чтобы получить проекции в одной плоскости (плоскости чертежа) необходимо и профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. В результате получим трехкартинный комплексный чертеж (эпюр Монжа), показанный на рис. 1.3, б. Так как ось ОY разворачивается вместе с двумя плоскостями П₁ и П₃ , то на комплексном чертеже ее изображают дважды.

Из этого следует важное правило взаимосвязи проекций. А именно, исходя из рис. 1.3, а, в математической форме его можно записать в виде: А₁А_x = ОА_y = А_zА₃. Следовательно, в текстологическом виде оно звучит так: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции указанной точки до оси ОZ. Тогда по двум любым проекциям точки можно построить третью. Горизонтальную и фронтальную проекции точки А связывает вертикальная линия связи, а фронтальную и профильную проекции – горизонтальная.

В связи с тем, что комплексный чертеж представляет собой свернутую в плоскости модель пространства, на нем нельзя изобразить проецируемую точку (за исключением случаев, когда ее положение совпадает с одной из проекций). Исходя из этого, следует иметь в виду, что на комплексном чертеже мы оперируем не самими геометрическими объектами, а их проекциями.