Жай сандар және олардың қасиеттері
8-анықтама.Бүтін  саны 0 мен
саны 0 мен 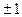 -ден өзге болса және
-ден өзге болса және 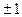 мен
мен 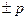 сандарынан басқа бөлгіштері болмаса, жай сан деп аталады.
сандарынан басқа бөлгіштері болмаса, жай сан деп аталады.
Мысалы, 2,3,5,7,11,13,17,19,23,29 сандары алғашқы оң жай сандар болса -2,-3,-5,-7,-11,-13,-17,-19,-23,-29 алғашқы теріс жай сандар болып табылады.
9-анықтама.Бүтін 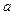 саны мен 0 мен
саны мен 0 мен 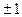 -ден өзге болса және
-ден өзге болса және 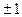 мен
мен 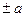 сандарынан басқа да бөлгіштері болса, құрама сан деп аталады.
сандарынан басқа да бөлгіштері болса, құрама сан деп аталады.
Мысалы, 4,6,8,9,10 сандары құрама сандар. Жай санның анықтамасынан бірталай салдарлар шығады. Алдағы уақытта тұжырымдарды оң жай сандарға қатысты қарастырамыз.
15-теорема. Егер  жай сан болса, онда кез келген
жай сан болса, онда кез келген 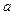 саны не
саны не  санына бөлінеді, не
санына бөлінеді, не  мен өз ара жай болады.
мен өз ара жай болады.
Дәлелдеуі. Шынында да, анықтама бойынша,  санының екі бөлгіші 1 және
санының екі бөлгіші 1 және  бар, сондықтан
бар, сондықтан 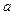 мен
мен  сандарының ортақ бөлгіші не 1 саны, не
сандарының ортақ бөлгіші не 1 саны, не  саны болуы мүмкін. Егер ортақ бөлгіші
саны болуы мүмкін. Егер ортақ бөлгіші  болса, онда
болса, онда 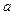 саны
саны  -ға бөлінеді, ал ортақ бөлгіші 1 болса, онда
-ға бөлінеді, ал ортақ бөлгіші 1 болса, онда 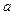 мен
мен  өз ара жай сандар болады.
өз ара жай сандар болады.
16-теорема. Егер екі немесе бірнеше бүтін сандардың көбейтіндісі жай санға бөлінсе, онда бұл санға көбейткіштердің кемінде біреуі бөлінеді.
Дәлелдеуі. Математикалық индукция әдісімен дәлелдейміз. Әуеліекі 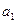 және
және 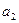 сандарының көбейтіндісін қарастырайық. Егер
сандарының көбейтіндісін қарастырайық. Егер 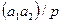 болса, онда
болса, онда 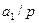 немесе
немесе 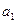 саны
саны  -ға бөлінбейді.
-ға бөлінбейді. 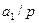 болса, онда теорема дәлелденді. Ал, егер
болса, онда теорема дәлелденді. Ал, егер 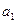 саны
саны  -ға бөлінбесе, онда, жоғарыдағы теорема бойынша,
-ға бөлінбесе, онда, жоғарыдағы теорема бойынша, 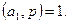 Онда 8-теорема бойынша
Онда 8-теорема бойынша 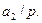 Енді теорема, көбейткіштер саны
Енді теорема, көбейткіштер саны 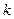 -дан кіші болғанда дұрыс деп есептеп, олардың саны
-дан кіші болғанда дұрыс деп есептеп, олардың саны 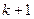 болғанда да дұрыстығын дәлелдейік.
болғанда да дұрыстығын дәлелдейік.
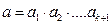
көбейтіндісін қарастырайық. Бұл көбейтіндіні көбейтудің ассоциативтігін пайдаланып, екі көбейтінді түрінде өрнектеуімізге болады.
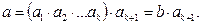
Ал, екі көбейткіш үшін теорема дұрыс болғандықтан 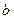 немесе
немесе 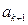 сандарының бірі
сандарының бірі  -ға бөлінеді. Егер
-ға бөлінеді. Егер 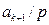 болса теорма дәлелденді. Егер
болса теорма дәлелденді. Егер 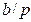 болса, индуктивтік ұйғарым бойынша,
болса, индуктивтік ұйғарым бойынша, 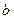 саны
саны 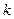 көбейткіштен тұратын болғандықтан,
көбейткіштен тұратын болғандықтан, 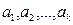 сандарының бірі
сандарының бірі  -ға бөлінеді. Теорема толық дәлелденді.
-ға бөлінеді. Теорема толық дәлелденді.
17-теорема. Кез келген бүтін сан, кем дегенде бір жай санға бөлінеді.
Дәлелдеуі. Математикалық индукция әдісін пайдаланайық.
1. 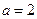 болса, онда теорема дұрыс. Себебі 2 саны, жай сан 2-ге бөлінеді.
болса, онда теорема дұрыс. Себебі 2 саны, жай сан 2-ге бөлінеді.
2. 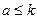 болғанда теореманы дұрыс деп есептеп,
болғанда теореманы дұрыс деп есептеп, 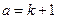 болғанда да дқрыстығын дәлелдейік.
болғанда да дқрыстығын дәлелдейік.
3. 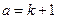 болсын. Егер
болсын. Егер 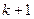 жай сан болса, онда ол
жай сан болса, онда ол 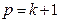 жай санына бөлінетіндіктен, теорема дәлелденген болады. Егер құрама сан болса,онда
жай санына бөлінетіндіктен, теорема дәлелденген болады. Егер құрама сан болса,онда 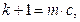
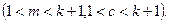 Ал
Ал 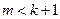 болғандықтан, индуктивтік ұйғарым бойынша,m саны үшін теорема дұрыс, яғни ол кем дегенде бір жай
болғандықтан, индуктивтік ұйғарым бойынша,m саны үшін теорема дұрыс, яғни ол кем дегенде бір жай  санына бөлінеді. Онда бөлінгіштің қасиеті бойынша
санына бөлінеді. Онда бөлінгіштің қасиеті бойынша 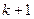 саны да
саны да  -ға бөлінеді. Теорема дәлелденді.
-ға бөлінеді. Теорема дәлелденді.
Біз қарастырып отырған бүтін сандар сақинасының структуралық ерекшелігі мына теоремамен өрнектеледі.
18-теорема. Кез келген бірден өзге бүтін сан не жай сан, немесе ақырлы жай сандардың көбейтіндісі түрінде бір ғана тәсілмен өрнектеледі.
Дәлелдеуі. 1. 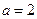 болсын. Онда 2 жай сан болғандықтан теоремадағы тұжырым
болсын. Онда 2 жай сан болғандықтан теоремадағы тұжырым 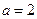 үшін дұрыс.
үшін дұрыс.
2.Енді теоремадағы тұжырым 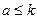 болғанда дұрыс деп есептеп,
болғанда дұрыс деп есептеп, 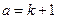 болғанда дұрыстығын дәлелдейік.
болғанда дұрыстығын дәлелдейік.
3. 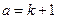 бүтін санын қарастырайық. Егер
бүтін санын қарастырайық. Егер 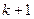 жай сан болса, онда оны екі санның көбейтіндісі түрінде өрнектей аламыз:
жай сан болса, онда оны екі санның көбейтіндісі түрінде өрнектей аламыз:
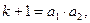
мұндағы,
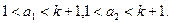
Ал, 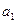 және
және 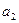 сандары
сандары 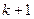 -ден кіші болғандықтан, индуктивтік ұйғарым бойынша, ол сандарға қатысты теоремадағы тұжырым орындалады; яғни
-ден кіші болғандықтан, индуктивтік ұйғарым бойынша, ол сандарға қатысты теоремадағы тұжырым орындалады; яғни 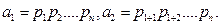 Демек,
Демек, 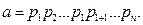
Жалғыздығын да индукция әдісімен дәлелдейміз.
1. 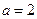 болсын. 2 жай сан болғандықтан,ол басқа сандар көбейтіндісі түрінде жіктелмейді. Демек,
болсын. 2 жай сан болғандықтан,ол басқа сандар көбейтіндісі түрінде жіктелмейді. Демек, 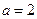 болғанда тұжырым дұрыс.
болғанда тұжырым дұрыс.
2. Тұжырым 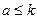 болғанда дұрыс деп есептеп,
болғанда дұрыс деп есептеп, 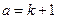 болғанда дұрыстығын дәлелдейік.
болғанда дұрыстығын дәлелдейік.
3. 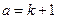 болсын, егер
болсын, егер 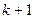 жай сан болса, онда ол жай сандар көбейтіндісіне жіктелмейді. Енді
жай сан болса, онда ол жай сандар көбейтіндісіне жіктелмейді. Енді 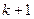 құрама сан болсын және ол жай сандар көбейтіндісі түрінде екі тәсілмен жіктеледі дейік:
құрама сан болсын және ол жай сандар көбейтіндісі түрінде екі тәсілмен жіктеледі дейік:
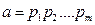 және
және 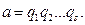
Онда 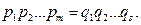 Бұл теңдіктің сол жағындағы өрнек жай сан
Бұл теңдіктің сол жағындағы өрнек жай сан 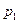 -ге бөлінетіндіктен, оң жағындығы өрнек те
-ге бөлінетіндіктен, оң жағындығы өрнек те 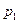 -ге бөлінеді. Онда, 15- теорема бойынша,
-ге бөлінеді. Онда, 15- теорема бойынша, 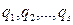 көбейткіштерінің бірі
көбейткіштерінің бірі 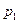 -ге бөлінеді.
-ге бөлінеді. 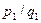 дейік. Ал
дейік. Ал 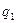 жай сан болғандықтан
жай сан болғандықтан 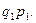 Жоғарыдағы теңдіктің екі жағын да
Жоғарыдағы теңдіктің екі жағын да 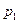 -ге бөлсек
-ге бөлсек
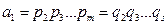
теңдігін аламыз.
Ал 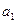 саны
саны 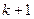 -ден кіші болғандықтан, индуктивтік ұйғарым бойынша, ол жай сандар көбейтіндісі түрінде жалғыз тәсілмен өрнектеледі, яғни, m=s. Демек,
-ден кіші болғандықтан, индуктивтік ұйғарым бойынша, ол жай сандар көбейтіндісі түрінде жалғыз тәсілмен өрнектеледі, яғни, m=s. Демек, 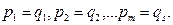
Кез келген құрама санының жай көбейткіштерге жіктелуінде, кейбір
көбейткіштердің тең болуы мүмкін.
Айталық 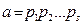 жіктелуіне
жіктелуіне 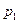 саны
саны 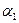 рет,
рет, 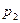 саны
саны 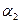 рет т.с.с. ақырында
рет т.с.с. ақырында 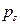 саны
саны 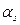 рет енеді делік, онда
рет енеді делік, онда 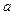 санын
санын
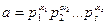 (4)
(4)
түрінде жаза аламыз, мұндағы 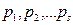 сандары
сандары  -ның әр түрлі жай бөлгіштері, ал
-ның әр түрлі жай бөлгіштері, ал 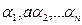 -натурал сандар. Әдетте
-натурал сандар. Әдетте 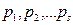 сандарын өсу реті бойынша орналастырылады.Осы (4) өрнек
сандарын өсу реті бойынша орналастырылады.Осы (4) өрнек  санының канондық жіктелуі деп аталады. Бұл өрнекті
санының канондық жіктелуі деп аталады. Бұл өрнекті  санын факторизациялау деп те атайды.
санын факторизациялау деп те атайды.
Мысалы, 432 санының канондық жіктелуі 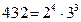 болады. Санның канондық жіктелуін білгеннен кейін, бір санның екінші санға бөлінгіштік критерийін тағайындауға болады. Айталық
болады. Санның канондық жіктелуін білгеннен кейін, бір санның екінші санға бөлінгіштік критерийін тағайындауға болады. Айталық  саны с санына бөлінеді дейік:
саны с санына бөлінеді дейік:
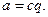
Сонда с санының канондық жіктеуіндегі әрбір жай сан  санының жіктеуіне де қатысуы тиіс және керісінше, с саны
санының жіктеуіне де қатысуы тиіс және керісінше, с саны  санының бөлгіші болғандықтан,
санының бөлгіші болғандықтан,  санының канондық жіктеуіндегі жай сандарға ғана бөлінуге тиісті. Сонымен бірге, с санының жіктеуіндегі жай бөлгіштің қай-қайсысыныңда дәреже көрсеткіші, осы жай санының
санының канондық жіктеуіндегі жай сандарға ғана бөлінуге тиісті. Сонымен бірге, с санының жіктеуіндегі жай бөлгіштің қай-қайсысыныңда дәреже көрсеткіші, осы жай санының  санының канондық жіктеуіндегі дәреже көрсеткішінен артпауы тиіс. Бұдан мынандай маңызды қорытынды шығады:
санының канондық жіктеуіндегі дәреже көрсеткішінен артпауы тиіс. Бұдан мынандай маңызды қорытынды шығады:
1-салдар. Егер  санының канондық жіктеуі
санының канондық жіктеуі
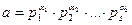
болса, онда мұның кез келген с бөлгішінің жіктеуі
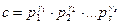
болады, мұнда 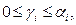
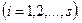
Канондық жіктеуі берілгеннен кейін, екі не бірнеше санының ең үлкен ортақ бөлгішін және ең кіші ортақ еселігін табуға болады. а және b сандарының канондық жіктеулері белгілі болсын.
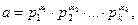
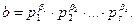
Мұндағы, 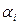 және
және 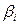 сандары нольге де тең болуы мүмкін. Онда а және b сандарының канондық жіктеулерінің екеуін де бірдей
сандары нольге де тең болуы мүмкін. Онда а және b сандарының канондық жіктеулерінің екеуін де бірдей 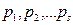 жай сандар арқылы өрнектеуімізге болады.
жай сандар арқылы өрнектеуімізге болады.
2-салдар. а және b сандарының ең үлкен ортақ бөлгіші төмендегіше анықталады:
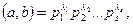
мұнда 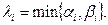
Мысалы, 360 және 96 сандарының канондық жіктелуі
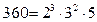 және
және 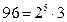
белгілі, енді осы екі санның ең үлкен ортақ бөлгішін табу керек болсын. Жай екі және үш сандары берілген екі санның да ал, 5 саны тек 360 санының жіктелуіне еніп отыр. Олай болса, жай 2 және 3 сандарының еі кіші 23 және 31 дәрежелерінің көбейтіндісі ізделінді, ең үлкен ортақ бөлгіші болып табылады

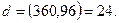 3-салдар. а және b сандарының ең кіші ортақ еселігі төмендегіше анықталады:
3-салдар. а және b сандарының ең кіші ортақ еселігі төмендегіше анықталады:
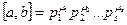
мұнда 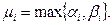
Алдыңғы мысалда жай 2,3,5, сандары 360-пен 96 сандарының кемінде біреуінің жіктеуіне еніп отыр, атап айтқанда 25,32,51 –ең үлкен дәрежелер. Сондықтан
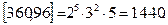
Үш не одан артық сандардың ең үлкен ортақ бөлгіші және ең кіші ортақ еселігі де осылайша табылады.
Енді  санының бөлгіштерінің табу мәселесімен шұғылданайық, атап айтқанда осы санның барлық бөлгіштерінің санын табайық.
санының бөлгіштерінің табу мәселесімен шұғылданайық, атап айтқанда осы санның барлық бөлгіштерінің санын табайық.
19-теорема. Егер  санының канондық жіктеуі
санының канондық жіктеуі 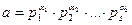 болса, онда
болса, онда  санының барлық натурал бөлгіштерінің саны
санының барлық натурал бөлгіштерінің саны 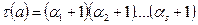 формуласымен анықталады.
формуласымен анықталады.
Дәлелдеуі. 18-теореманың 1-ші салдары бойынша,  санының кез келген с бөлгіші төмендегіше өрнектеледі:
санының кез келген с бөлгіші төмендегіше өрнектеледі:
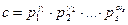
мұнда,
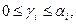
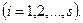 Сондықтан,
Сондықтан,  санының барлық натурал бөлгіштерінің санын анықтау үшін,
санының барлық натурал бөлгіштерінің санын анықтау үшін, 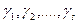 -терден тұратын және
-терден тұратын және 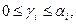
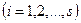 теңсіздігін қанағаттандыратын, жиынтықтардың мүмкін комбинациясын есептеуіміз керек.
теңсіздігін қанағаттандыратын, жиынтықтардың мүмкін комбинациясын есептеуіміз керек. 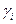 -лардың қабылдай алатын, жоғарыдағы теңсіздікті қанағаттандыратын мәндерінің саны
-лардың қабылдай алатын, жоғарыдағы теңсіздікті қанағаттандыратын мәндерінің саны 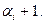
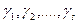 көрсеткіштері
көрсеткіштері 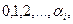

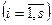 мәндерін бір-бірінен тәуелсіз қабылдайтындықтан және жай сандар көбейтіндісіне жіктеу жалғыз болатындықтан (18-теорема), көрсеткіштер мәндерінің әр түрлі
мәндерін бір-бірінен тәуелсіз қабылдайтындықтан және жай сандар көбейтіндісіне жіктеу жалғыз болатындықтан (18-теорема), көрсеткіштер мәндерінің әр түрлі 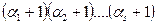 комбинациясын шығарып аламыз. Демек,
комбинациясын шығарып аламыз. Демек,  санының барлық бөлгіштерінің санын
санының барлық бөлгіштерінің санын 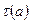 деп белгілесек, ол мына формуламен табылады
деп белгілесек, ол мына формуламен табылады
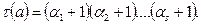
мысалдар, 1. Айталық 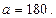 Онда
Онда 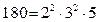 болғандықтан,
болғандықтан,
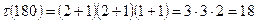
2.Айталық 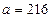 санының бөлгіштерін табу керек болсын. Ол санның канондық жіктеуі
санының бөлгіштерін табу керек болсын. Ол санның канондық жіктеуі 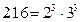 болады. Олай болса,
болады. Олай болса,
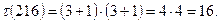
Енді, осы 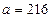 санының бөлгіштерін тауып көрейік. Ол үшін, жалпы формуланы жазамыз
санының бөлгіштерін тауып көрейік. Ол үшін, жалпы формуланы жазамыз 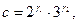 мұнда
мұнда 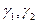 -лер 0,1,2,3 мәндерін қабылдайды.
-лер 0,1,2,3 мәндерін қабылдайды. 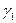 мен
мен 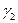 мәндерін өз ара комбинациялай отырып, сәйкес бөлгіштерді табамыз:
мәндерін өз ара комбинациялай отырып, сәйкес бөлгіштерді табамыз:
Мұнда жазу керек
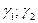 | ||||
| 0;0 | ||||
Енді берілген  санының барлық бөлгіштерінің қосындысын есептеуге формула қорытып шығарайық.
санының барлық бөлгіштерінің қосындысын есептеуге формула қорытып шығарайық.
20-теорема. Егер  санының, канондық
санының, канондық 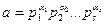 жіктеуі белгілі болса, онда бұл санның барлық натурал бөлгіштерін қосындысы
жіктеуі белгілі болса, онда бұл санның барлық натурал бөлгіштерін қосындысы
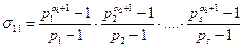
формуласымен анықталады.
Дәлелдеуі.  санының кез келген с бөлгіші, 18-теореманың 3-ші салдары бойынша,
санының кез келген с бөлгіші, 18-теореманың 3-ші салдары бойынша, 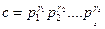 түрінде жіктелетінін білеміз. Енді s жақшадан тұратын мына өрнекті
түрінде жіктелетінін білеміз. Енді s жақшадан тұратын мына өрнекті 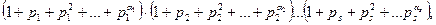 (5)
(5)
қарастырайық. Бұл өрнектің 1-ші жақшасы 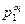 санының барлық
санының барлық 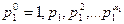 бөлгіштерінің қосындысы, ал 2-ші жақша
бөлгіштерінің қосындысы, ал 2-ші жақша 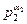 санының барлық
санының барлық 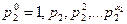 бөлгіштерінің қосындысы т.с.с. Сонымен, ақырында соңғы жақша
бөлгіштерінің қосындысы т.с.с. Сонымен, ақырында соңғы жақша 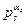 санының барлық
санының барлық 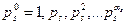 бөлгішгіштерінің қосындысы. (5) өрнектегі жақшаларды ашып, мына қосындыны табамыз:
бөлгішгіштерінің қосындысы. (5) өрнектегі жақшаларды ашып, мына қосындыны табамыз:
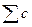 (6)
(6)
бұл қосындының әрқайсысы  санының бөлгіші болатын
санының бөлгіші болатын
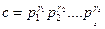
түріндегі әр түрлі қосылғыштардан құралған
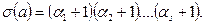
бөлгіштердің қосындысы болып табылады. Демек, (6) өрнек  санының барлық
санының барлық 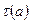 бөлгіштерінің қосындысы болмақ. Ал егер (5) өрнектің әрбір жақшасын өз алдына жеке есептеп алатын болсақ, онда біз бірден
бөлгіштерінің қосындысы болмақ. Ал егер (5) өрнектің әрбір жақшасын өз алдына жеке есептеп алатын болсақ, онда біз бірден  санының барлық бөлгіштерінің қосындысын беретін формуланы табамыз:
санының барлық бөлгіштерінің қосындысын беретін формуланы табамыз:
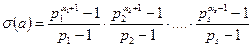
Мысалдар. 1. 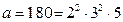 санының барлық бөлгіштерінің қосындысын табайық.
санының барлық бөлгіштерінің қосындысын табайық. 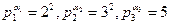 болғандықтан, жоғарыдағы формула бойынша,
болғандықтан, жоғарыдағы формула бойынша,
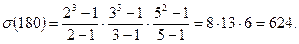
2. 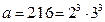 санының барлық бөлгіштерінің қосындысын табайық.
санының барлық бөлгіштерінің қосындысын табайық.