Запишите решение заданий уровня В с полным обоснованием. В1. Найдите значение производной функции в точке x0 = 2001
В1. Найдите значение производной функции 
в точке x0 = 2001.
В2.Укажите количество промежутков убывания функции 
, заданной на отрезке [0; 2π].
В3.Найдите максимум функции 
.
Запишите решение заданий уровня С с полным обоснованием
С1. При каком значении параметра а функция 
имеет минимум в точке x0 = 1?
С2.Определите промежутки возрастания функции .
Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной »
Вариант 12
Запишите вариант правильного ответа заданий уровня А
А1.Найти производную функции 
.
а)  | б)  | в)  | г)  |
А2.Найти производную функции 
.
а)  | б)  | в)  | г)  |
А3.Найти производную функции 
.
а)  | б)  | в)  | г)  |
А4.Вычислить 
, если f(x)= 
.
а) 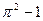 | б)2π+1 | в)2 π-1 | г)2 π |
А5.Найти значение производной функции 
в точке x0=1
а)  | б)  | в)  | г)  |
А6.Найти значение производной функции 
в точкеx0=0.
| а) 1 | б) 0 | в) 0,5 | г) -1 |
А7.Найти тангенс угла наклона касательной, проведенной к графику функции 
в его точке с абсциссой x0= -2.
| а) 1 | б) 2 | в) 0 | г) -1 |
А8.Найти угловой коэффициент касательной, проведенной к графику функции 
в его точке с абсциссой x0=1.
| а) 1,4 | б) 2 | в) 7 | г) 12 |
А9.Найти угловой коэффициент касательной, проведенной к графику функции 
в его точке с абсциссой x0=0.
| а) -3 | б) -2 | в) 2 | г) 3 |
А10.Координата материальной точки изменяется с течением времени по закону 
. Найдите скорость точки в момент времени t=2.
| а) 48 | б) 54 | в) 70 | г) 88 |
А11.Найдите значение производной 
в точке x0=0.
а)  | б) 0 | в) 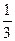 | г) 1 |
А12.Найдите значение производной функции 
в точке t0=1.
| а) -8 | б) 8 | в) 6 | г) -6 |