Бұрыштық модуляция

Фазалық модуляция x(t) біріншілік сигналдың фазасының пропорционалды өзгерісі.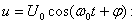

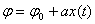. (8.1)

Бұл жерде а-пропорциональдық коэффиценті. Фазалық модуляция кезінде тербеліс амплитудасы өзгермейді, сондықтан да тербелістің фазалық модуляциясы былай өрнектеледі:

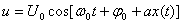. (8.2)

Егер де модуляция гармоникалық сигналмен өрнектелетін болса x(t) =Xsin Ωt, онда лездік фаза

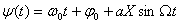. (8.3)

(8.3) алғашқы екі қосылғыштар модуляцияланбаған тербелістің фазасын анықтайды, ол үшіншісі-модуляция әсерінен тербелістің фазасының өзгеруін. Фаза модуляцияланған тербеліс 8.1- суреттегі векторлық диаграммамен сипатталады. Ол жазықтықта құрылған, сағат тілінің бойымен айналатын бұрыштық жиілігі w₀. Модуляцияланбаған тербеліске жылжымайтын вектор U₀ сәйкес келеді.

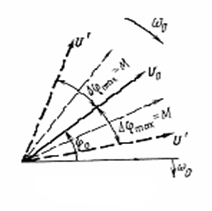
8.1 Сурет - Фаза модуляцияланған тербелістің векторлық диаграммасы

U векторының шеткі орналасулары U’ және U’’ деп белгіленген. Модуляцияланған тербелістің фазасының модуляцияланбаған тербелістің фазасынан максималды ауытқуы

M=∆φ_max=aX. (8.4)

Модуляция индексі деп аталады. Модуляция индексі М модуляциланбаған сигналдың Х амплитудасына пропорционал. Ол сол деңгейде ФМ тербелісті де сипаттайды, модуляция коэффициенті т ретінде-АМ тербелісі.

(8.4) қолдана отырып, ФМ тербелісті (8.2)былай көшіреміз

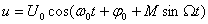. (8.5)

ФМ тербелістің лездік жиілігі

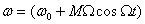. (8.6)

Осылайша ФМ тербелісі әртүрлі уақыт мезетінде әртүрлі лездік жиіліктерге ие, ω₀ тасушы тербелістің жиілігінен 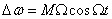шамасына айрықшаланатын, бұл ФМ тербелісті жиілік бойынша модуляцияланған деп қарастыруға мүмкіндік береді. ω жиіліктің ω₀ -дан үлкен ауытқуы жиілік девиациясы ∆ω_Д деп аталады. (8.6) сәйкес

∆ω_д =MΩ және ∆f_Д =MF. (8.7)

Жиіліктік модуляция біріншілік сигналға x(t) тасушының лездік жиілігінің өзгерісне пропорционал

ω=ω₀+ax(t). (8.8)

Бұл жерде а-пропорционалдық коэффициенті. ЖМ тербелістің лездік фазасы.

ЖМ тербелістің аналитикалық теңдігін амплитуданың тұрақты екенін ескере отырып былай жазуға болады

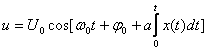. (8.9)

Қарапайым жағдайда модуляциялар гармоникалар тербеліспен лездік жиілік 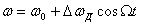, бұл жерде 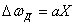–жиілік девиациясы, яғни ω₀, тасушы жиіліктен максималды ауытқуы, модуляция әсерінен. Бұл ЖМ тербелістің (8.9) сәкес аналитикалық теңдеуі былай болады .

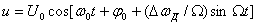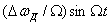қосылғышы ЖМ кезінде алынатын фазасы өзгерісін сипаттайды. Бұл ЖМ тербелістің модуляция индексі бар ФМ тербелісі деп қарастыруға мүмкіндік береді.

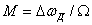, (8.10)

және оны (8.9) ұқсас етіп жазсақ

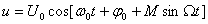. (8.11)

Бұл айтылғаннан, ФМ және ЖМ тербелістердің ортақ ұқсастықтарын байқауға болады. (8.11) түрінде тербеліс ФМ-ң шешімі бола алады,сонымен қатар ЖМ гармонкалық біріншілік сигналдың да. Одан басқа ФМ және ЖМ бірдей параметрлерімен сипатталады, өзара байланысқан бірдей қатынастармен (8.7) және (8.10). Белгіленген жиіліктік және фазалық модуляциялардың ұқсастықтарымен қоса олардың айырмашылықтары да бар, біріншілік сигналдан F М және ∆f_Д шамаларының тәуелділіктерінің әртүрлі қасиетімен байланысты -ФМ кезінде модуляция индексі F жиіліккке тәуелді емес, ал жиілік девиациясы (1.23) сәйкес F–ке пропорционал;

-ЖМ кезінде жиілік девиациясы жиілікке тәуелді емес, ал модуляция индексі сәйкес F–ке кері пропорционал.

Егер де әртүрлі жиіліктерден тұратын санынан тұратын модуляция күрделі сигналмен іске асырылатын болса, онда жиіліктік және фазалық модуляция араларында айырмашылық қатты байқалады. Айтылғанды түсіндіру үшін 8.2 б,в суретінде ЖМ және ФМ тербелістерінің графиктері тұрғызылған, (8.2 а суретті қара) x(t) сигналына сәйкес үшбұрышты формада. ЖМ кезінде x(t) жоғарлауы w жоғарлауына байланысты және керісінше ФМ кезінде ∆φ(t) = ax (t), a ω= ω₀+adx/dt.

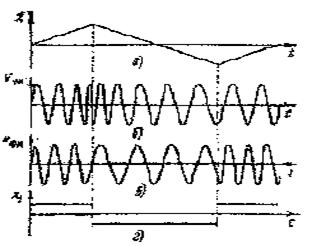
8.2 Сурет

Сондықтанда dx/dt>0, облыстарында лездік жиілік тасушыдан 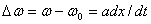шамасына үлкен; dx/dt>0 облыстарында ФМ тербелістің ω₀ жиілігі ∆ω шамасына аз. Осылайша ФМ x(t) үшбұрышты формалы сигналмен ЖМ x₁(t) тікбұрышты формалы сигналы сәйкес келеді (8.2 суретті қара). Жалпы бұрыштық модуляциямен кез-келген тербелісі ФМ біріншілік сигнал x(t) ретінде, сонымен қатар ЖМ х₁(t)=dx/dt сигналының шешімі ретінде алуға болады. Осы айтылғанға қосатын нәрсе, жиіліктік және фазалық модуляция олардың орындау тәсілдерінде де айрықшаланады.