В древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел.
I V X L C D M
1 5 10 50 100 500 1000
Используя циферблат часов с римской нумерацией, установите, как обозначается число 8?

А) VIII Б) VII В) IIIV Г) XIII
4. Пётр I ввёл в России привычные для нас цифры. Сколько цифр небходимо, чтобы записать любое натуральное число?

А) две Б) девять В) десять Г) бесконечно много
5. Укажите неверное утверждение:
А) В натуральном ряду каждое следующее число на 1 больше предыдущего
Б) Самое маленькое натуральное число – нуль
В) Натуральный ряд бесконечен, наибольшего числа в нем нет
Г) Класс единиц натурального числа составляют три первые цифры справа
На свитке должны быть записаны три числа, стоящие в натуральном ряду после числа 80 010 и три числа, стоящие в натуральном ряду до числа 8 998. Найдите лишнее число.

А) 8 989 Б) 80 001 В) 80 011 Г) 8 001
Разбейте на классы и прочитайте число 9780521062.
А) девять миллиардов семьдесят восемь миллионов пятьсот двадцать одна тысяча шестдесят два
Б) девяносто семь миллионов восемьсот пятьдесят две тысячи сто шестдесят два
В) девятьсот семьдесят восемь миллионов пятьсот двадцать одна тысяча шестдесят два
Г) девять миллиардов семьсот восемьдесят миллионов пятьсот двадцать одна тысяча шестдесят два
8. Знаки «+» и «-» впервые появились в печати в 1489 году в книге немец-кого математика, который также первым напечатал таблицу умножения. Расшифруйте его имя и фамилию:
А) Ян Вадмин Б) Ям Виднам В) Ян Видман Г) Ив Яндман
9. Умножение столбиком придумал английский математик Уильям Оутред. Замените звёздочки цифрами так, чтобы получился правильно выполнен-ный пример на умножение. В ответе укажите результат примера.
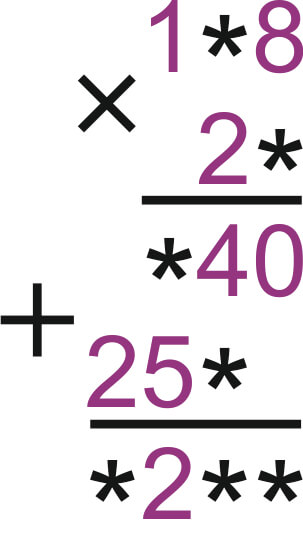

А) 3 200 Б) 2 200 В) 2 250 Г) 3 250
10. У пятиклассника Димы коллекция динозавров: травоядных – чётное количество, а хищных – нечётное. Диме подарили ещё двух динозавров. Сколько динозавров не может быть у Димы?


А) 15 Б) 28 В) 27 Г) 25
11. Вычислите удобным способом: 65·17+28·20+83·65+20·72.
А) 5 800 Б) 850 В) 9 500 Г) 8 500
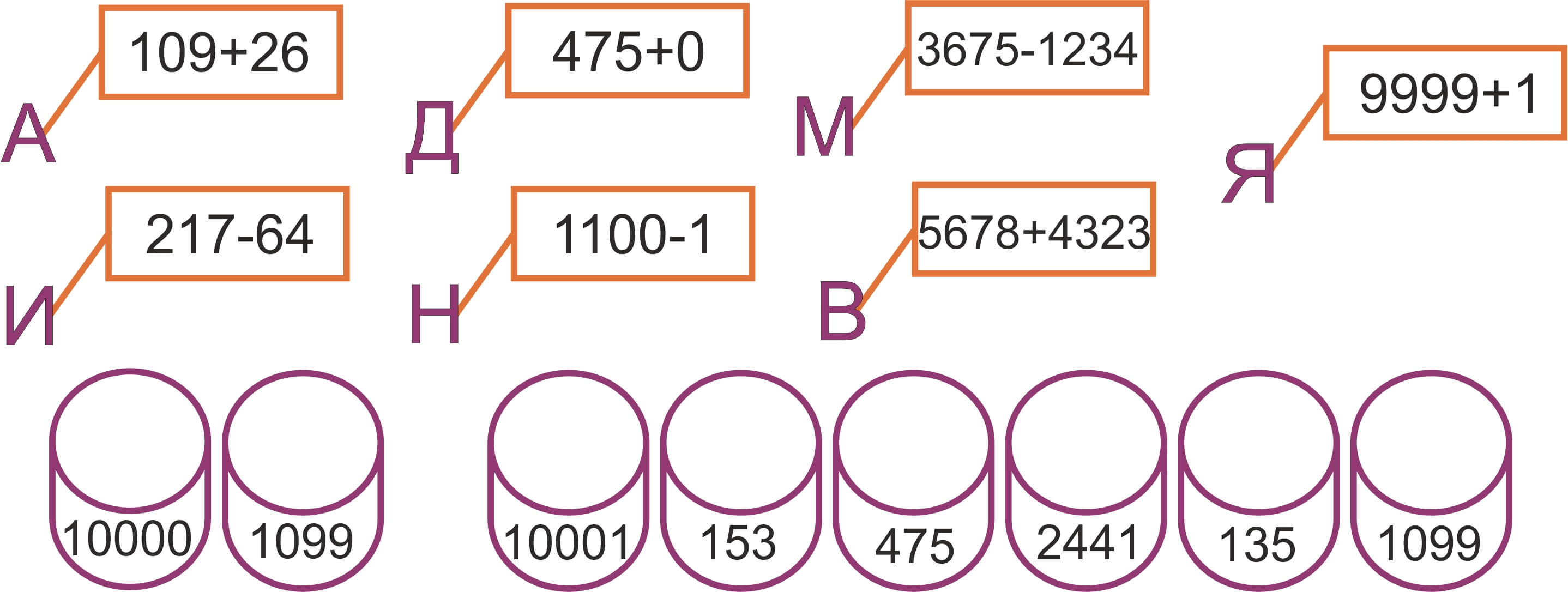
12. Скобки – это особые «знаки препинания» в математическом языке, которые были введены в обиход саксонским математиком Готфридом Лейбницем. Установите соответствие:
| Выражение |  | Значение выражения | ||
| А | 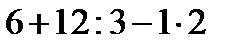 | |||
| Б | 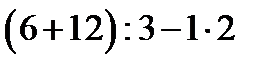 | |||
| В | 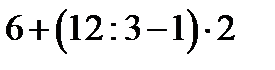 | |||
| Г | 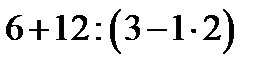 | |||
А) А - 2, Б - 4, В - 1, Г - 2 Б) А - 5, Б - 4, В - 1, Г - 2
В) А - 2, Б - 1, В - 4, Г - 5 Г) А - 3, Б - 4, В - 5, Г - 2
Обозначение неизвестных буквами латынского алфавита x, y, z пришло в математику благодаря французу Рене Декарту.

Решите уравнение: 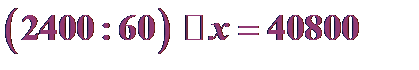 .
.
А) 100 Б) 1020 В) 102 Г) 120
Первые пятьдесят чисел натурального ряда записали без пропусков и получили число 12345678910111213141516...47484950. Определите количество классов в записи этого числа.
А) 18 Б) 29 В) 31 Г) 30
В древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел.

При записи числа иероглифы единицы, десятка, сотни и т. д. писались столько раз, сколько в этом числе единиц соответствующего разряда. Разряды писались справа налево (слева – меньшие, справа – большие) – в обратном порядке, чем у нас сейчас. Например, запись числа 102 934 выглядит так:

А числа 25 400 000 так:

В каком случае число не соответствует записи в древнеегипетской нумерации?
| Число | Запись | |
| А) | 13 642 |  |
| Б) | 23 641 |  |
| В) | 23 451 |  |
| Г) | 32 641 |  |
