Алгоритмы эффективного кодирования неравновероятных взаимозависимых символов сообщений
Устранение взаимной зависимости символов источника сообщения может быть осуществлено путем укрупнения алфавита исходного источника сообщения. Для этого подлежащие кодированию сообщения последовательно разбиваются на двух-, трех- или n-знаковые сочетания (блоки), вероятности которых известны, а затем эти сочетания кодируются в соответствии с алгоритмами Шеннона-Фено или Хаффмена.
Недостаток этого алгоритма состоит в том, что при его использовании не учитываются связи между символами, входящими в состав соседних сочетаний (блоков).
Этот недостаток может быть устранен кодированием по методу диаграмм, триграмм или в общем случае k-грамм. k-граммой называют последовательность из k смежных символов сообщения. При k=2 сочетание смежных знаков называют диаграммой, при k=3 — триграммой и т.д.
В процессе кодирования по методу k-грамм производят непрерывное последовательное перемещение k-граммы по сообщению с шагом равным одному символу. Этот процесс (получение 3-х k-грамм) иллюстрируется рис. 2.3, где xi - символы сообщения.
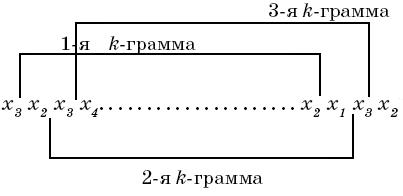 Рис 2.3. Процесс непрерывного последовательного перемещения k-граммы по сообщению. |
Если вероятности появления различных k-грамм известны, то их эффективное кодирование, в частности, может быть выполнено по алгоритмам Шеннона-Фено или Хаффмена. Конкретное значение k выбирается исходя из степени взаимозависимости между символами сообщения и сложности технической реализации кодирующих и декодирующих устройств.