Исследование законов распределения случайных процессов

Цель работы: изучение аппаратурного метода измерения плотности распределения вероятностей случайных процессов и исследование преобразования плотностей распределения типовыми звеньями радиотехнических устройств. Изучение некогерентного приема сигналов (приема по огибающей).

Опыт 1. Изучение аппаратурного метода измерения плотности распределения вероятностей случайного процесса с помощью фотооптического анализатора

1.1 Вероятность ошибки при некогерентной обработке сигналов в каналах с нормальной аддитивной помехой [1]

В ряде случаев нецелесообразно применять сложное и дорогое приемное устройство, обеспечивающее высокую помехоустойчивость по отношению к флуктуационному шуму в канале связи. Часто можно ограничиться использованием более простых методов обработки смеси сигнала и шума и получить необходимую достоверность приема. Кроме того, из-за случайного изменения параметров каналов (нестабильности характеристик передающего устройства, изменения параметров среды распространения
и т.д.) под действием случайных факторов параметры принятых сигналов также становятся случайными. Если фаза принимаемых сигналов случайна, то прием называют некогерентным.

Когерентный и некогерентный способы приема могут применяться для любых видов модуляции сигналов. Однако для простых двоичных АМ- и ЧМ-сигналов когерентный прием обычно не используется, так как его аппаратурная реализация сложнее некогерентного приема, и если уж идти на такое усложнение, то целесообразнее применять ФМ-сигналы. В случае некогерентного приема используются АМ- и ЧМ-сигналы.

При передаче измерительной информации простыми АМ-сигналами с пассивной паузой на вход приемника поступает колебание

,

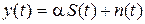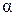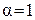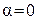где – модулирующий параметр, принимающий значения: или , соответственно, при наличии и отсутствии сигнала; 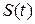– переданный сигнал; 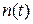– аддитивная помеха.

На интервале времени 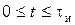( 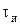- длительность импульса в канале связи) сигнал .

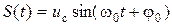На рис. 3.1 приведена упрощенная структура приемника, осуществляющего некогерентный прием простых АМ-сигналов по огибающей колебаний, приходящих на вход приемника. Линейную фильтрацию на входе детектора выполняют входные цепи приемника, усилитель высокой частоты, преобразователь и усилитель промежуточной частоты. Линейный фильтр обеспечивает основную селекцию сигнала от помехи. Алгоритм принятия решения основан на сравнении мгновенного значения огибающей посылок сигнала с некоторым напряжением – оптимальным порогом. В соответствии с этим правилом принимается решение о том, что сигнал есть, если напряжение огибающей превысит оптимальный порог; если не превысит – сигнала нет.

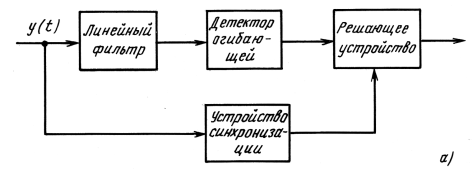
Рисунок 3.1 – Схема некогерентного приема AM-сигналов

Полагаем, что априорные вероятности появления 1 и 0 одинаковы, т.е. P(0) = P(1) = 0,5. Тогда вероятность ошибки при передаче одного символа сообщения P_ош = 0,5 (P_л.т + P_пр)., где – соответственно вероятности, ложной теории и пропуска сигнала.

Обозначим огибающую напряжения на выходе детектора при наличии сигнала через u_с.ш, а при его отсутствии – через u_ш.

Тогда условные вероятности ошибок можно записать в виде

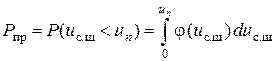; (3.1)

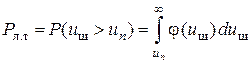, (3.2)

где 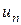– пороговое напряжение, j(u_с.ш) и j(u_ш) – одномерные функции распределения вероятностей огибающих u_с.ш и u_ш соответственно.

Как известно [1], распределение огибающей смеси синусои­дального колебания с амплитудой u_с и нормального шума подчиняется закону Райса

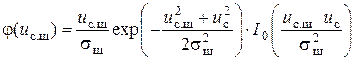, (3.3)

где s_ш² — дисперсия шума; I₀ — функция Бесселя нулевого порядка от мнимого аргумента.

Распределение (3.3) также называют обобщенным распределением Релея. При отсутствии сигнала распределение (3.3) принимает вид

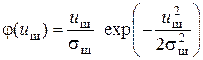, так как I₀ =1. (3.4)

Полученная зависимость носит название «распределение Релея» и описывает плотность вероятностей огибающей нормального шума.

Введем обозначения: u_с.ш /s_ш = h; u_с /s_ш = q; u_ш /s_ш = z.

Тогда (3.3) и (3.4) примут вид

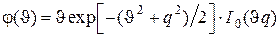; (3.5)

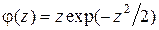. (3.6)

На рис. 3.2 приведены зависимости j(h) и j(z). При увеличении q кривая j(h) смещается вправо, приближаясь к нормальному закону распределения.

С учетом (3.1), (3.2) и (3.5), (3.6) выражение для вероятности ошибки при некогерентном приеме простых АМ-сигналов можно записать в виде

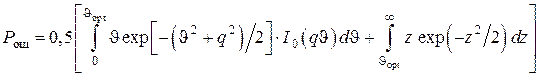. (3.7)

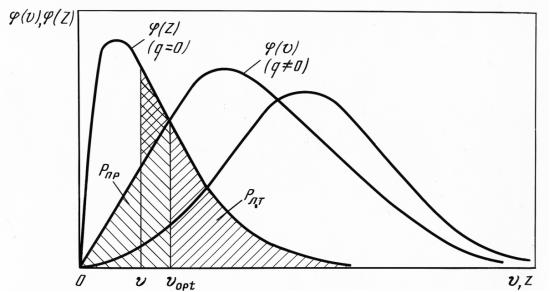
Рисунок 3.2 – Дифференциальные законы распределения
колебаний на выходе детектора огибающей

Выражение для оптимального порога можно получить, исследуя функцию (3.7) на минимум. Однако эту задачу можно решить проще. Как видно из рис. 3.2, минимальное значение вероятности ошибки обеспечивается при выборе порога на пересечении кривых j(z) и j(h). Любое изменение порога увеличивает полную вероятность ошибки на значение, соответствующее площади зачерченного криволинейного треугольника. Анализ различных способов модуляции при некогерентном приеме двоичных сигналов показывает, что для достаточно больших отношений сигнал/шум (h > 4) и оптимальном пороге вероятность ошибки будет определяться следующими выражениями:

при приеме АМ-сигналов ;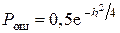

при приеме ЧМ-сигналов ;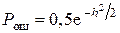

при использовании относительной фазовой модуляции .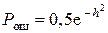

Тогда общее выражение для вероятности ошибки при некогерентном приеме двоичных сигналов можно записать в виде

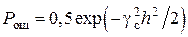, (3.8)

где g_с – коэффициент, зависящий от способа модуляции сигналов.

1.2 Ознакомление с принципом действия и функциональной схемой фотооптического анализатора плотности распределения мгновенных значений случайного процесса в режиме автоматического измерения (экспресс-анализ) [2]

Рассматривая некоторый стационарный эргодический случайный процесс , можно показать, что существует определенная связь между плотностью распределения и относительным временем пребывания реализации внутри интервала 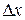(между уровням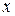и и 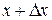), рис.3.3.

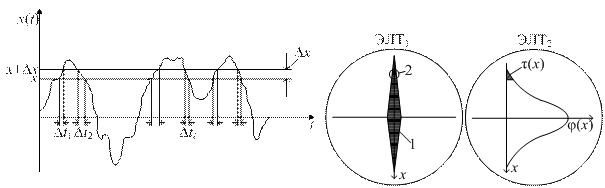
а) б) в)

Рисунок 3.3 – Иллюстрация зависимости плотности распределения вероятностей 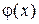от относительного времени пребывания реализации внутри интервала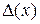

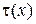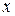Она заключается в том, что относительное время пребывания реализации (рис. 3.3 а) между уровнями и 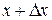дает оценку вероятности:

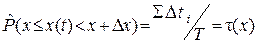, (3.9)

где 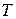– интервал наблюдения; 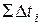– суммарное время пребывания процесса в интервале 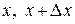за время .

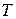Для достаточно малых 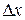оценка плотности 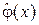распределения вероятностей мгновенных значений случайного процесса

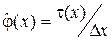. (3.10)

Таким образом, при 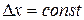измерение 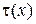дает оценку плотности вероятности .

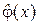В фотооптическом анализаторе электрическая реализация случайного процесса преобразуется с помощью электронно-лучевой трубки ЭЛТ₁ осциллографа в светящееся изображение 1 (рис. 3.3 б). Яркость 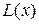этого изображения в различных точках будет неодинакова и зависит от относительного времени пребывания луча в этих точках, т.е. пропорциональна числу электронов, попадающих в эти точки в единицу времени (закон Ленарда).

Преобразуя яркость 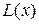в данной точке изображения 1 в величину электрического напряжения 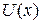с помощью фоторезистора 2 (рис. 3.3 б), получим количественную, легко измеряемую электрическую величину, по которой можно оценить плотность 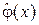, например, на экране другой электронно-лучевой трубки ЭЛТ₂ (рис. 3.3 в), преобразовав 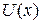в амплитуду отклонения луча.

Принцип действия фотооптического преобразователя основан, таким образом, на цепочке преобразований

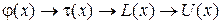. (3.11)

Функциональная схема фотооптического анализатора в режиме автоматического измерения плотности распределения вероятностей (экспресс-анализ) случайного процесса приведена на рис. 3.4.

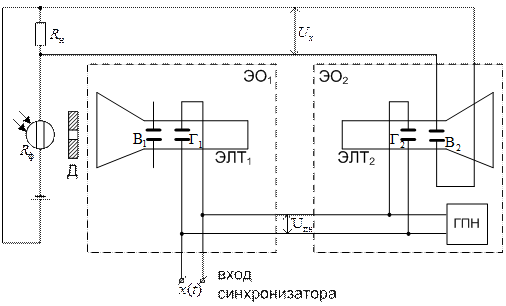
Рисунок 3.4 – Функциональная схема фотооптического анализатора

Анализатор состоит из двух осциллографов ЭО₁ и ЭО₂ с электронно-лучевыми трубками ЭЛТ₁ и ЭЛТ₂. Исследуемый процесс подается на горизонтально отклоняющие Г₁ пластины ЭЛТ₁, перед экраном которой установлена диафрагма Д и фоторезистор 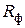. К этим же пластинам подводится пилообразное напряжение 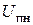генератора пилообразного напряжения ГПН осциллографа ЭО₂. Напряжение 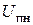вызывает медленное автоматическое перемещение изображения на ЭЛТ₁ относительно диафрагмы Д. Напряжение 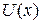, пропорциональное плотности 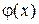, подается с резистора 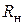на вертикально отклоняющие пластины B₂ осциллографа ЭО₂, а на пластины Г₂ подается напряжение 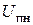. Луч осциллографа ЭО₂ совершает перемещение в системе двух координат:

а) вертикальная ось – ;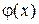

б) горизонтальная ось – .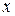

Изображение на экране ЭЛТ₂ является, таким образом, оценкой плотности распределения вероятностей 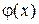.