Опишите, как свести вычисление определителя порядка n к вычислению определителя порядка n-1
В строке 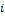 получить все нули за исключением элемента
получить все нули за исключением элемента 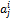 , затем найти алгебраическое дополнение этого элемента.
, затем найти алгебраическое дополнение этого элемента.
Дайте определение обратной матрицы.
Обратная матрица 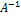 – такая матрица, при умножении на которую квадратная матрица с определителем, отличным от нуля, даёт единичную матрицу.
– такая матрица, при умножении на которую квадратная матрица с определителем, отличным от нуля, даёт единичную матрицу.
31. Какие матрицы имеют обратную?
Только квадратные матрицы с определителем, отличным от нуля.
32. Как найти элемент 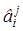 обратной матрицы?
обратной матрицы?
Для этого нужно найти алгебраическое дополнение элемента 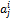 .
.
33. Как найти матрицу Х из уравнения А·Х=В, если detА≠0?
Для этого нужно найти обратную матрицу 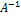 и умножить на неё обе части уравнения, приписывая её слева.
и умножить на неё обе части уравнения, приписывая её слева.
34. Как найти матрицу Х из уравнения Х·А=В, если detА≠0?
Для этого нужно найти обратную матрицу 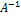 и умножить на неё обе части уравнения, приписывая её справа.
и умножить на неё обе части уравнения, приписывая её справа.
35. Объясните, как понимаете слова: «Определена внутренняя операция над элементами множества А».
Значит, задан закон, согласно которому двум элементам из множества 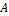 ставится в соответствие третий элемент также из этого множества. В линейном пространстве это сумма.
ставится в соответствие третий элемент также из этого множества. В линейном пространстве это сумма.
36. Объясните, как понимаете слова: «Определена внешняя операция над элементами множества А».
Значит, задан закон, согласно которому одному элементу из множества 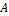 и другому элементу из множества
и другому элементу из множества 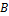 ставится в соответствие третий элемент из множества
ставится в соответствие третий элемент из множества 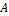 . В линейном пространстве это произведение.
. В линейном пространстве это произведение.
Сформулируйте аксиомы, характеризующие внутреннюю операцию в определении линейного пространства.
1) 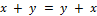 ;
;
2) 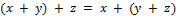 ;
;
3) 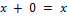 ;
;
4) 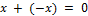 ;
;
5) 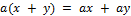 .
.
Сформулируйте аксиомы, характеризующие внешнюю операцию в определении линейного пространства.
1) 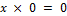 ;
;
2) 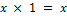 .
.
Сформулируйте аксиомы, связывающие внешнюю и внутреннюю операции в определении линейного пространства.
1) 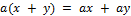 ;
;
2) 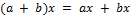 .
.
Дайте определение понятий линейной комбинации, линейно зависимой и линейно независимой систем векторов.
Линейная комбинация – вектор, являющийся суммой нескольких векторов, умноженных на не обязательно одинаковые коэффициенты.
Линейно зависимая система векторов – система векторов, которая возможна при наличии таких коэффициентов при векторах, что их сумма равна нулевому вектору. В такой системе хотя бы один вектор является линейной комбинацией других.
Линейно независимая система векторов – система векторов, в которой ни один вектор не является линейной комбинацией других.
Сформулируйте теорему о необходимом и достаточном условии линейной зависимости системы векторов.
Для того чтобы система векторов была линейно зависима, необходимо и достаточно, наличие хотя бы одного вектора, являющегося линейной комбинацией других.
