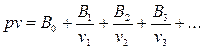I.5. Реальные свойства газа. Уравнение состояния реального газа

При высоких давлениях и очень низких температурах использовать уравнение Менделеева-Клапейрона нельзя и следует использовать уравнения состояния реального газа.

Известно много уравнений состояния реального газа, каждое из которых имеет свою область применения. Рассмотрим некоторые из этих уравнений. Наиболее теоретически обоснованными являются уравнения состояния ре­ального газа в виде ряда с вириальными коэффициентами:

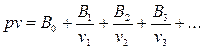(23)

Здесь, B₀, B₁, B₂, B₃, … - вириальные коэффициенты, определяемые опытным путём. На практике ограничиваются первыми тремя вириальными коэффициентами.

Уравнение (23) имеет и другие формы записи. Впервые уравнение состояния реального газа было получено в 1887 году голландцем Ван-дер-Ваальсом:

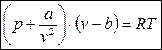(24)

Здесь, b – это поправка на собственный объём молекул (коволюм), 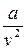- поправка на силу межмолекулярного взаимодействия (внутреннее давление).

Уравнение (24) не учитывает ассоциации молекул, но оно впервые позволило опи­сать с единой позиции процессы с фазовыми переходами, например, сжижение газа при его изотермическом сжатии.

Изотермический процесс идеального газа записывается в виде уравнения pv = const, которое в pv – координатах изображается как гипербола первого порядка (рис.3)

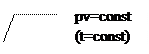
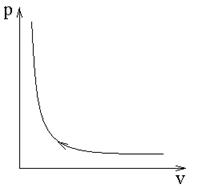
рис.3. Изотермическое сжатие идеального газа

р

V

рис.4. Изотермическое сжижение реального газа при его сжатии.

Обозначения: - - - - - расчет по уравнению Ван-дер-Ваальса.

- опыт.

Как показывают многочисленные опыты, процесс изотермического сжижения газа имеет типичный вид, представленный на рис.4.

В целом, уравнение Ван-дер-Ваальса качественно правильно и удовлетвори­тельно количественно описывает процессы реального газа.

Заштрихованные области - области метастабильного состояния вещества.

Ассоциация молекул – объединение двух и более молекул в группы. При высоких температурах поправка на межмолекулярное взаимодействие мала, и ею можно пренебречь.

Поэтому, для артиллерийской практики, где p = 30-700 МПа и температура 500-3000°K используется уравнение Дюпре:

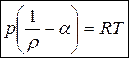(25)

где 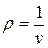- плотность, α – коволюм.

Уравнение Дюпре – частный случай уравнения (24) при внутреннем давлении равном 0.

Для практических расчётов используют уравнение Майера-Боголюбова:

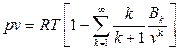(26)

Здесь, B_k – k-ый вириальный коэффициент. Как показали опыты, для реального газа под разряжением достаточно взять k=1, то есть:

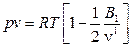(27)

Для расчёта процессов с водяным паром широко используется уравнение Вукаловича-Новикова:

,

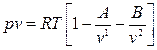Здесь A и B – эмпирические коэффициенты.

Известны и другие уравнения состояния реального газа. Все эти уравнения (Ван-дер-Ваальса, Дюпре и т.д) являются частными случаями уравнения состояния реального газа в виде ряда с вириальными коэффициентами: