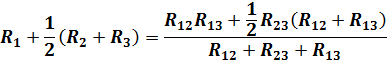Закон Ома. Напряжение на резисторе равно произведению силы тока на его сопротивление.

Откуда

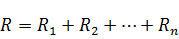
Т.е. при последовательном соединении резисторов их сопротивления складываются.

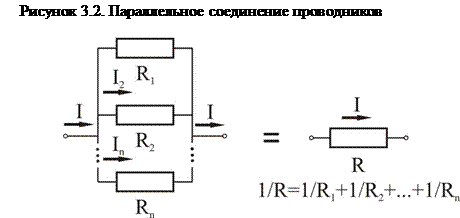Параллельное соединение. Когда несколько проводников или резисторов соединены параллельно(рисунок 3.2), то уже напряжение на всех резисторах одинаковое, и равно U, разности потенциалов между входом и выходом .

Ток I на входе и на выходе цепи равен сумме сил токов в отдельных ветвях параллельной цепи:

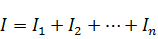
Подставляя в это выражение I=U/R и I_i=U/R_i получаем

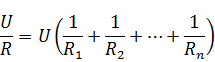
Откуда

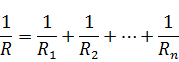
Т.е. при параллельном соединении складываются величины обратные сопротивлению-проводимости. Сопротивление параллельной цепи всегда меньше сопротивления любого резистора входящего в нее.

Эквивалентные схемы. Многие цепи можно значительно упростить, шаг за шагом заменяя участки параллельного и последовательного соединения их эквивалентными сопротивлениями.

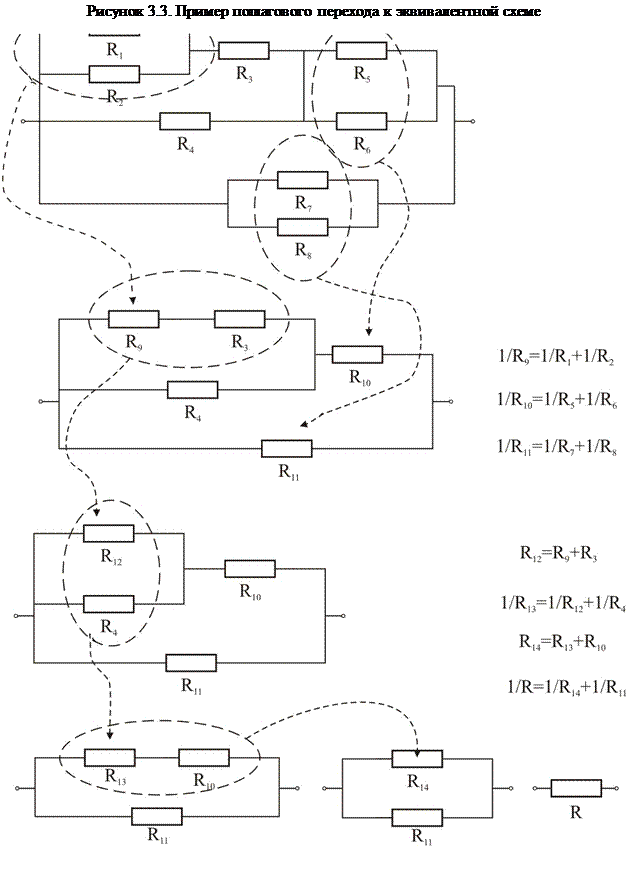
Однако не любую электрическую цепь можно представить как комбинацию последовательных и параллельных соединений. При рассмотрении таких «сложных» цепей нужно руководствоваться следующими правилами:

Закон Ома. Напряжение на резисторе равно произведению силы тока на его сопротивление.

2. Правило сложение токов. В любом узле алгебраическая сумма токов равна нулю: сумма втекающих токов равна сумме вытекающих.

3. Сумма напряжений на отдельных участках цепи при проходе по любому контору от «входа» к «выходу» равна приложенному напряжению.

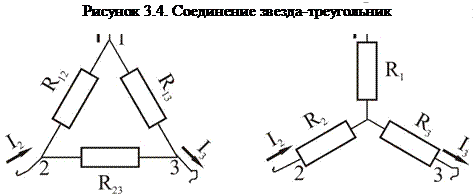Звезда-треугольник. Рассмотрим ряд примеров. В некоторых случаях расчет сложной цепи значительно упрощается, если треугольник сопротивлений заменить звездой сопротивлений, т. е. тремя ветвями, имеющими дополнительный общий узел (рисунок 3.4.). В других случаях расчета цепей встречается необходимость звезду заменить треугольником. Эти взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами 1, 2 и 3 треугольника и звезды токи I₁, I₂, I₃ в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.

Сопротивления эквивалентной звезды R₁, R₂, R₃ находятся в определенных соотношениях с сопротивлениями треугольника R₁₂, R₂₃, R₁₃. Для выяснения этой зависимости допустим сначала, что в вершине 1 произошел обрыв подводящего провода и, следовательно, ток I₁=0. Сопротивления между двумя оставшимися присоединенными вершинами 2 и 3 для обеих схем должны быть одинаковы, чтобы были соответственно равны токи I₂ и I₃ в обеих схемах. После обрыва в вершине 1 сопротивления R₂ и R₃ звезде соединены последовательно, а в треугольнике сопротивления R₁₃ и R₁₂ соединенные последовательно, образуют одну ветвь с суммарным сопротивлением R₁₃+ R₁₂, параллельно которой подключено сопротивление R₂₃. Поэтому можно написать

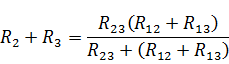
Рассуждая аналогично для случая обрыва в вершине 2, при котором ток I₂ = 0, а затем провода 3, при котором ток I₃=0, получим аналогичные выражения:

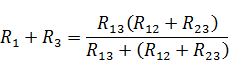
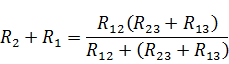
Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника R₁₂,R₂₃, R₁₃, требуется определить сопротивления лучей эквивалентной звезды R₁, R₂, R₃ . Для этого составим полусумму левых и правых частей двух последних уравнений