Примеры. Задача 1. В партии товара 80% изделий стандартны
Задача 1. В партии товара 80% изделий стандартны. Случайным образом отобрано пять изделий. Найти вероятность того, что три из них стандартны; стандартных не менее трех; стандартно хотя бы одно.
Каково наивероятнейшее число стандартных изделий и соответствующая ему вероятность?
Решение: Обозначим: событие А — взятое изделие стандартно. По условию 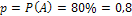 ;
; 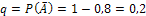 ;
;
а) 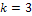
Так как число повторных испытаний 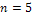 , применим формулу Бернулли.
, применим формулу Бернулли.
Таким образом,
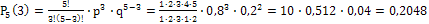 .
.
б) 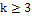 , то есть
, то есть 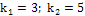 .
.
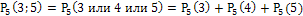 ;
;
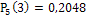 – найдено выше.
– найдено выше.
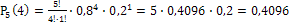 .
.
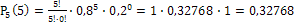 .
.
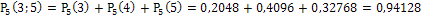 .
.
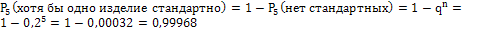 .
.
Найдем наивероятнейшее число 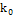
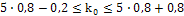 ;
;
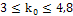 .
.
Единственное целое число из этого промежутка равно 4.
Итак, ему 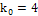 соответствует вероятность:
соответствует вероятность: 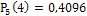 - она была найдена выше.
- она была найдена выше.
Ответ: 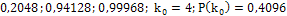 .
.
Задача 2. Вероятность того, что изделие прослужит гарантийный срок, равна 0,9. Организация закупила 60 изделий. Найти вероятность того, что прослужит гарантийный срок: а) половина всех изделий; б) не менее 52 и не более 58 изделий; в) хотя бы одно изделие.
Каково наивероятнейшее число изделий, которые прослужат гарантийный срок? Чему равна его вероятность?
Решение: Дано 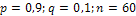 .
.
Так как 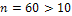 , то применим формулы Лапласа.
, то применим формулы Лапласа.
а) 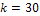 . По локальной формуле Лапласа находим:
. По локальной формуле Лапласа находим:
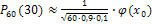 , где
, где 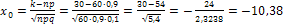 .
.
По таблице приближения 1: 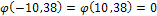 . Здесь учтено, что функции
. Здесь учтено, что функции 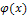 - четная. Тогда
- четная. Тогда 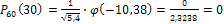 .
.
б) 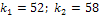 . По интегральной формуле Лапласа
. По интегральной формуле Лапласа
 , где
, где 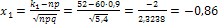 ,
, 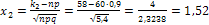 .
.
Значения 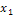 и
и 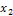 округляем до двух знаков после запятой.
округляем до двух знаков после запятой.
По таблице приложения 2 находим значения функции 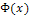 , учитывая, что она нечетная:
, учитывая, что она нечетная:
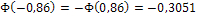 ;
;
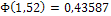 .
.
Таким образом.
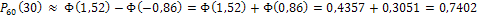 .
.
в) 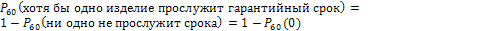 .
.
По локальной формуле Лапласа найдем:
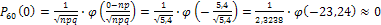 ,
,
так как по таблице приложения 1: 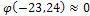 .
.
Если вероятность события равна нулю, оно называется НЕВОЗМОЖНЫМ. Отсюда следует, что 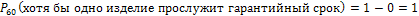 , то есть это событие обязательно произойдет, оно называется ДОСТОВЕРНЫМ.
, то есть это событие обязательно произойдет, оно называется ДОСТОВЕРНЫМ.
Наивероятнейшее число 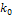 :
:
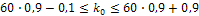 ;
;
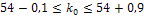 ,
,
то есть 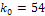 . Соответствующую ему вероятность находим по локальной формуле Лапласа:
. Соответствующую ему вероятность находим по локальной формуле Лапласа: 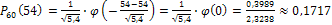 ,
,
где 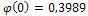 - значение найдено по таблице приложения 1.
- значение найдено по таблице приложения 1.
Ответ: 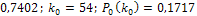 .
.
Задача 3. Вероятность выиграть по лотерейному билету равна 0,3. Какова вероятность, что выиграет, по крайней мере один из четырех купленных билетов?
Решение: 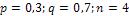 .
.
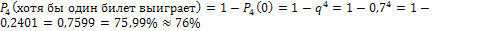 .
.
Ответ: 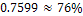 .
.
