Первая теорема двойственности

Связь между оптимальными решениями пары двойственных задач устанавливается с помощью теоремы двойственности. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить ее отсутствие.

Основное неравенство теории двойственности.

Пусть имеется пара двойственных задач. Для любых допустимых решений X=(x₁, x₂,…, x_n), Y=(y₁, y₂,…, y_m) исходной и двойственной задач справедливо неравенство

L(Х)£Z(Y) или 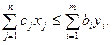(7)

Доказательство. Умножим неравенства системы ограничений исходной задачи AX£B соответственно на переменные двойственной задачи y₁, y₂,…, y_m и сложим правые и левые части полученных неравенств, получим

YAX £ BY = Z(Y) (8)

Аналогично преобразовав систему ограничений двойственной задачи AY³C путем умножения обеих частей на переменные исходной задачи x₁, x₂,…, x_n и последующего их сложения, получим

ХAY ³ CХ = L(Х) (9)

Т.к. левые части неравенств (8) и (9) представляют одно и тоже выражение AXY, тогда получим CХ = L(Х) £ AXY £ BY = Z(Y)

В силу свойства транзитивности неравенств получим доказываемое неравенство .¨

Теперь можно перейти к признакам оптимальности решений.

Теорема (достаточный признак оптимальности).

Если X^*=(x^*₁, x^*₂,…, x^*_n) и Y^*=(y^*₁, y^*₂,…, y^*_m) – допустимые решения взаимно двойственных задач, для которых выполняется равенство

L(Х^*)= Z(Y^*),

то Х^* - оптимальное решение исходной задачи I, а Y^* - двойственной задачи II.

Доказательство. Пусть Х₁ – любое допустимое решение исходной задачи I. Тогда на основании основного неравенства (8) получим L(Х₁)£Z(Y^*)=| по условию |= L(Х^*), т.е.

L(Х₁)£ L(Х^*).

Однако Х₁ – произвольное решение задачи I, отсюда следует, что Х^* - оптимальное решение исходной задачи I. Аналогично доказывается, что решение оптимально для задачи II. ¨

Возникают вопросы: всегда ли для каждой пары двойственных задач есть одновременно оптимальные решения; возможна ли ситуация, когда одна из двойственных задач имеет решение, а другая нет. Ответ на эти вопросы дает следующая теорема.

Первая (основная) теорема двойственности. Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:

L_max= Z_min или L(Х^*)= Z(Y^*),

где X^*=(x^*₁, x^*₂,…, x^*_n), Y^*=(y^*₁, y^*₂,…, y^*_m) – оптимальные решения взаимно двойственных задач.

Если одна из задач не имеет решения в виду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.

Доказательство. Из первой части утверждения теоремы (которую мы принимаем без доказательства) следует, что равенство L(Х^*)= Z(Y^*) является не только достаточным признаком оптимальности решений (доказанным выше), но и необходимым признаком оптимальности решений взаимно двойственных задач.

Утверждение второй части докажем методом от противного.

Предположим, что в исходной задаче линейная функция не ограничена сверху, т.е. L_max=µ, а условия двойственной задачи не противоречивы, т.е. существует хотя бы одно допустимое решение Y=(y₁, y₂,…, y_m). Тогда в силу основного неравенства теории двойственности L(Х)£Z(Y), что противоречит условию неограниченности L(Х). Следовательно, при L_max=µ в исходной задаче допустимых решений в двойственной задаче быть не может.¨

Экономический смысл первой (основной) теоремы двойственности. План производства X^*=(x^*₁, x^*₂,…, x^*_n) и набор цен (оценок) ресурсов Y^*=(y^*₁, y^*₂,…, y^*_m) оказывается оптимальным тогда и только тогда, когда прибыль от продукции, найденная при “внешних” (известных заранее) ценах с₁, с₂,…,с_n, равна затратам по “внутренним” (определенным только из решения задачи) ценам y₁, y₂,…, y_m . Для всех же других планов Х и Y обеих задач в соответствии с основным неравенством L(Х)£Z(Y) теории двойственности прибыль от продукции всегда меньше (или равна) затрат на ресурсы.

Экономический смысл первой (основной) теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить продукцию по оптимальному плану X^*=(x^*₁, x^*₂,…, x^*_n) и получить максимальную прибыль F_max или продавать ресурсы по оптимальным ценам Y^*=(y^*₁, y^*₂,…, y^*_m) и возместить от продажи равные ей минимальные затраты на ресурсы Z_min.