По сопротивлению материалов

ЛАБОРАТОРНЫЕ РАБОТЫ

ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ

Студент_____________________

Группа______________________

20____/20____учебный год

Севастополь

620.10(076.5)

К 518

УДК 620.10(076.5)

Клыков А.Е., Наземцев А.П., Пичугова Л.Н.

К 518 Лабораторные работы по сопротивлению материалов. – Севастополь: СНУЯЭиП, 2012. – 56 с., ил.

Издание СНУЯЭиП, 2012

ИНСТРУКЦИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ ПРИ РАБОТЕ

В ЛАБОРАТОРИИ МЕХАНИЧЕСКИХ ИСПЫТАНИЙ

Перед началом работы необходимо ознакомиться с устройством ма-шин, приборов и помнить следующее:

1. Категорически запрещается прикасаться к токоведущим частям испытательных машин и приборов.

2. Если корпус машин (приборов) оказался под напряжением, их необходимо немедленно выключить и доложить об этом преподавателю или лаборанту.

3. Необходимо выполнять только ту работу, которая поручена, и при условии, что известны безопасные способы ее выполнения.

4. Если при включении машины слышно гудение электромотора, необходимо немедленно выключить машину и доложить преподавателю или лаборанту.

5. Категорически запрещается класть на испытательные машины инструменты, образцы и другие предметы.

С настоящей инструкцией ознакомился:

Подпись студента___________________

Методические указания к выполнению лабораторных работ

1. Каждый студент к началу лабораторной работы должен проработать

контрольные вопросы и рекомендуемую литературу.

2. Все расчеты, которые необходимо производить при оформлении лабораторной работы, выполняются с помощью калькулятора.

3. Отчет о выполненной лабораторной работе и ее зачет, как правило, должны полностью заканчиваться в часы занятий.

4. При защите отчетов студент должен показать знания основ теории, понимании физической сущности проведенных экспериментов и знакомство как с устройством испытательных машин и приборов, так и с постановкой лабораторных работ.

Перевод механических величин из технической системы

единиц в международную

1. Сила F: 1 кгс ≈ 10 Н = 10^-5 МН = 10^-2 кН.

2. Момент М (или Т): 1 кгс∙м ≈ 10 Нм.

3. Напряжения σ, τ и давление: 1 кгс/см² ≈ 0,1 МН/м² (МПа).

4. Удельный вес γ : 1г/см³ ≈ 0,01 МН/м³.

5. Площадь А : 1см² = 10^{-4 м2}.

6. Момент инерции I_x , I_xy , I_p :1см⁴ = 10^-8 м⁴.

7. Момент сопротивления W_x , W_p : 1 см³ = 10^{-6 м3} .

Лабораторная работа № 1

ОПРЕДЕЛЕНИЕ УПРУГИХ ПОСТОЯННЫХ СТАЛИ

Цель работы: Экспериментально определить модуль упругости

и коэффициент Пуассона для стали.

Задание для самостоятельной подготовки к работе

Подготовить ответы на предлагаемые к данной работе вопросы.

Литература

1. Конспект лекций.

2. Ямпольский Е.Д. Сопротивление материалов, 1972.

3. Феодосьев В.И. Сопротивление материалов. М., 1970.

1. Подготовка к испытанию

1.1. Испытательная машина и её характеристики:

марка __________________________

наибольшее создаваемое усилие ____________ тс _____________ кН

способ создания усилия ______________________________________

способ измерения нагрузки на образец _________________________

1.2. Устройство рычажно-стрелочного механического тензометра:

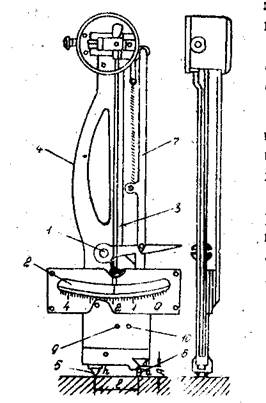
1 – фиксатор рычага и стрелки;

2 – шкала;

3 – стрелка, фиксирующая показания

тензометра;

4 – станина;

5 – неподвижная опора тензометра;

6 – подвижная опора (призма);

7 – рычаг, связанный возвратной пру-

жиной с подвижной опорой и

стрелкой.

Рис. 8.

1.3. Геометрические характеристики образца:

ширина в = ______см; толщина t = ______см;

площадь поперечного сечения А = _________см².

1.4. Установка продольного Т₁ и поперечного Т₂ тензометров на образце

(рис. 9).

Основные требования:

а) растягивающая сила должна быть направлена вдоль оси образца;

б) тензометр нельзя устанавливать в непосредственной близости от торцов и краев рабочей части образца.

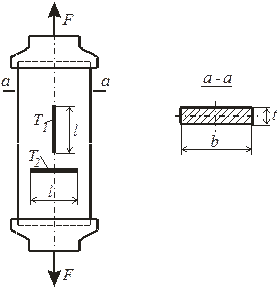
Рис. 9.

1.5. Кинематическая схема рычажного тензометра:

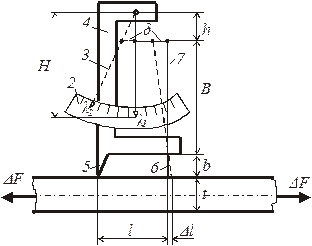
Δλ = λ₂ – λ₁; k = Δλ/Δl;

Δλ/H = δ/h; Δl/b = δ/B;

k = B∙H/b∙h

Рис. 10.

1.6. Параметры рычажного тензометра, используемого в лабораторной

работе:

база l = 20мм;

коэффициент увеличения k = 1000.

1.7. Определение максимальной нагрузки на образец.

По условию прочности действующее в образце напряжение σ не должно превышать предельно допускаемой величины [σ]:

σ = F/A ≤ [σ].

Допускаемое напряжение испытываемой стали [σ] = 1600кгс/см².

Находим максимальное усилие, которое может быть приложено к образцу:

F_max = [σ]∙A = _____________ = __________ кгс.

2. Результаты наблюдений

2.1. Журнал наблюдений

№№ ступ. нагр.	Нагрузка F , кгс	Ступень нагруж., ΔFi , кгс	Отсчеты по тензометрам
вдоль волокон	поперек волокон
отсчет λ1	разность отсчетов Δλ1	отсчет λ2	разность отсчетов Δλ2
Среднее значение ΔF = ______кгс	Средняя разность Δλ1 =_____мм	Средняя разность Δλ2 =_____мм

2.2. Определение модуля упругости Е:

а) абсолютное продольное удлинение образца на длине базы тензометра

Δl₁ = Δλ₁/k = __________________ = ___________мм

б) относительная продольная деформация

ε₁ = Δl₁/l = _____________________ = _____________

в) напряжение, соответствующее ступени нагружения ΔF = ______кгс,

σ = ΔF/A =__________=_____________кгс/см²;

г) модуль упругости материала

Е = σ/ε₁ = ______________ = __________ кгс/см² = __________МПа.

2.3. Определение коэффициента Пуассона:

а) абсолютная поперечная деформация образца на длине базы прибора

Δl₂ = Δλ₂/k _______________ = __________мм;

б) относительная поперечная деформация

ε₂ = Δl₂/l _________________= _________ мм;

в) коэффициент Пуассона

μ = ‌|ε₂/ε₁| = _____________________ = ___________

3. Выводы

3.1. В результате проделанной работы определены следующие значения упругих постоянных стали:

модуль упругости при растяжении Е = ______ кг/см² = _______МПа;

коэффициент Пуассона μ = ____________

3.2. Модуль упругости при сдвиге зависит от найденных упругих постоянных и определяется следующим образом:

G = E/2(1 + μ) = __________________________ = ___________ МПа.

Работу выполнил студент____________________

Оценка теоретических знаний____________________

Работу проверил____________________

«____»______________20 г.

Контрольные вопросы

1. В чем заключается физический и геометрический смысл модуля упругости?

2. Что представляет собой коэффициент Пуассона?

3. По какой формуле определяется модуль упругости в лабораторной работе?

4. Что такое абсолютное абсолютное удлинение и абсолютное укорочение?

5. Как определяются нормальные напряжения в поперечном сечении растянутого стержня?

6. Дать определение относительного удлинения.

7. Как называется параметр, являющийся коэффициентом пропорцио-нальности между нормальным напряжением σ и относительной деформацией ε ?

8. Дать определение относительного сужения.

9. Как связан коэффициент Пуассона с относительными изменениями размеров образца в продольном и поперечном направлениях?

10. Описать принцип работы и общее устройство рычажного тензометра.

11. Для какой цели создают предварительную нагрузку на образец?

12. Какими соображениями следует руководствоваться при определении максимальной силы, приложенной при испытании к образцу?

13. Как по показаниям тензометра определить деформацию образца?

14. Для чего необходима центровка образца?

15. Почему рекомендуется устанавливать тензометры с обеих сторон образца?

16. В каких пределах изменяется коэффициент Пуассона?

17. Каким материалам соответствуют крайние значения коэффициента Пуассона?

18. Какое свойство материала характеризует модуль упругости?

19. Какие параметры характеризуют жесткость стержня при растяжении или сжатии?

Лабораторная работа № 2

ИСПЫТАНИЕ МАЛОУГЛЕРОДИСТОЙ СТАЛИ НА РАСТЯЖЕНИЕ

Цель работы: 1. Получить диаграмму напряжений при растяжении.

2. Определить основные механические характеристики стали

3. Ознакомиться с устройством испытательной машины.

Задание для самостоятельной подготовки к работе

Подготовить ответы на предлагаемые к данной работе вопросы.

Литература

1. Конспект лекций.

2. Ямпольский Е.Д. Сопротивление материалов, 1972.

3. Феодосьев В.И. Сопротивление материалов. М., 1970.

1. Подготовка к испытанию

1.1. Испытательная машина и её характеристики (рис.1):

марка_____________________________

наибольшее разрывное усилие_________тс ________кН

способ создания усилия _________________________

способ измерения нагрузки на образец _____________

масштабы машинной диаграммы:

для нагрузок _m_F = ________кгс/см,

удлинений _ m_Δl = __________см/см.

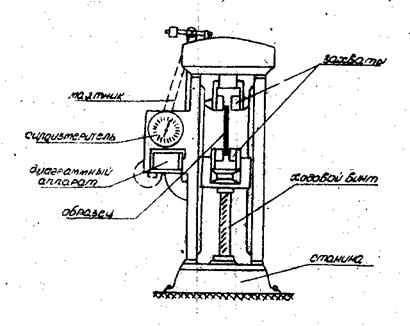
Рис.1.

1.2. Геометрические характеристики образца до испытания:

диаметр d_о = _____________________см;

рабочая длина l_о = ________________см;

площадь поперечного сечения А_о = ____________________см² .

1.3. Вид образца до испытания (пропорциональный цилиндрический образец, тип II, ГОСТ 1497-61)

Рис.2.

1.4. Масштабы перехода к напряжениям и и относительным деформациям:

масштаб напряжений m_σ = m_F / А_о = _________________кгс/см²∙см

_________________МПа/см;

масштаб относительных удлинений m_ε = 100∙m_Δl / l_о = _________% /см.

2. Результаты испытаний

2.1. Геометрические характеристики образца после разрыва:

конечный диаметр в районе шейки d_к = ________см;

конечная длина рабочей части l_к =______________см;

площадь поперечного сечения шейки А_ш =_________ = ________см² .

2.2. Вид образца после испытания

Рис.3.

2.3. Координаты y_i характерных точек машинной диаграммы, соответству-

ющие им усилия F_i = y_i ∙m_F и напряжения σ_i = y_i ∙m_σ :

Точка
Координата yi , см	______	______	______	______
Усилие Fi , кгс
Напряжение σi , МПа

2.4. Характеристики прочности материала:

1. Предел пропорциональности σ_п =___________МПа.

2. Предел текучести σ_т =___________МПа.

3. Предел прочности или временное сопротивление растяжению

σ_в =___________МПа.

4. Условное напряжение при разрыве σ_р =___________МПа.

5. Истинное напряжение при разрыве σ_ри =___________МПа.

2.5. Деформация образца на пределе пропорциональности (точка 1) при

модуле упругости материала Е = __________кгс/см² :

относительное удлинение ε_п = σ_п /E = _____________= _________;

абсолютное удлинение Δ l_п = ε_п∙l_o =____________=________см;

отрезок на оси x машинной диаграммы Δ l_пд = Δ l_п /m_Δl = _________см

= _________мм.

2.6. Остаточная деформация образца при разрыве:

абсолютное остаточное удлинение Δl_ост =___________см;

относительное остаточное удлинение ε_ост= Δl_ост /l_о =________=______;

отрезок на оси x машинной диаграммы Δl_остд = Δl_ост / m_Δl =_________=

=_________см.

2.7. Координаты x_i характерных точек машинной диаграммы и соответст-

вующие им относительные удлинения ε_i = x_i∙m_ε:

Точка
Координата, xi ,см
Относительное удлинение εi, %

2.8. Характеристики пластичности материала:

1. Относительное остаточное удлинение при разрыве

δ = 100∙(l_к – l_о )/ l_о = _________________=________%

2. Относительное остаточное сужение (уменьшение площади попереч-

ного сечения в месте шейки):

ψ = 100∙(А_о – А_ш)/ А_о = ___________

2.9. Характеристики вязкости материала:

1. Удельная работа, затраченная машиной на разрыв образца

w = 0,01η∙σ_в∙δ = ______________________=_______МНм/м³ ,

где η = 0,85 – коэффициент полноты диаграммы;

2. Полная работа

W = w∙l_o∙A_o = __________________=_________Hм.

2.10. Диаграмма условных напряжений при растяжении стали

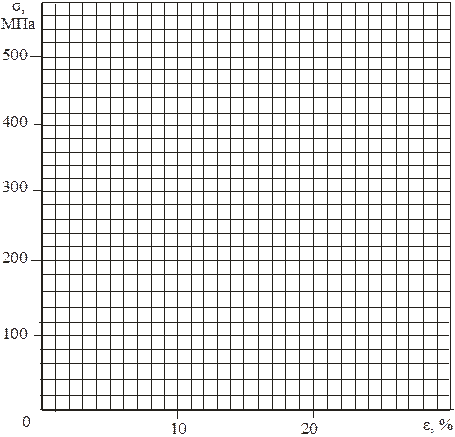
Рис.4.

3. Выводы.

3.1. Какой марке стали ориентировочно соответствует материал образца?

3.2. Какие напряжения являются опасными для данной стали ? Подсчитать коэффициент запаса прочности исследуемой стали, полагая допускаемое напряжение [σ] = 160МПа.

Работу выполнил студент____________________

Оценка теоретических знаний____________________

Работу проверил____________________

«____»______________20 г.

Контрольные вопросы

1. Какой вид нагружения называют растяжением?

2. По какой формуле определяют нормальные напряжения при

растяжении?

3. Записать два вида выражения закона Гука.

4. Каков примерный вид диаграммы условных напряжений для малоуглеродистых и легированных сталей?

5. Какова зависимость для вычисления удельной работы, затрачиваемой на разрыв образца?

6. Какие деформации называют упругими и остаточными?

7. Что такое предел упругости?

8. Что называют пределом пропорциональности?

9. Что называют пределом прочности или временным сопротивлением

растяжению?

10. В каких координатах строится машинная диаграмма при растяжении?

11. Что такое относительное остаточное удлинение?

12. Что называют относительным сужением площади поперечного сечения образца при разрыве?

13. В чем состоит сущность явления наклепа?

14. Как построить диаграмму условных напряжений при растяжении по машинной диаграмме?

15. Что называется пределом текучести?

16. На каком участке диаграммы растяжения соблюдается закон Гука?

17. Как зависит деформация образца от силы на пределе текучести?

18. Какой участок диаграммы соответствует стадии вторичного упрочнения?

19. На каком участке диаграммы формируется местное сужение образца?

20. По какому закону распределяются нормальные напряжения в поперечном сечении при растяжении?

21. В каком напряженном состоянии находится материал растянутого стержня?

22. По каким формулам определяются напряжения на наклонном сечении при растяжении?

23. В каких сечениях растянутого стержня возникают максимальные нормальные и касательные напряжения?

24. Каково условие прочности при растяжении?

25. Как определяется коэффициент запаса прочности для пластичных и хрупких материалов?

Лабораторная работа № 3

ИСПЫТАНИЯ НА СЖАТИЕ

Цель работы: 1. Сопоставить процессы деформирования и разрушения при

сжатии различных материалов (пластичных и хрупких,

изотропных и анизотропных).

2. Определить характеристики прочности при сжатии

испытуемых материалов.

3. Получить диаграммы напряжений при сжатии и сравнить

механические характеристики материалов.

Задание для самостоятельной подготовки к работе

Необходимо предварительно усвоить основные допущения, принятые в сопротивлении материалов, понятие о сплошном, однородном, изотропном и анизотропном теле.

Литература

1. Конспект лекций.

2. Ямпольский Е.Д. Сопротивление материалов, 1972.

3. Феодосьев В.И. Сопротивление материалов. М., 1970.

1. Подготовка к испытаниям

1.1. Испытательная машина и её характеристики:

машина______________________;

наибольшее создаваемое усилие______________тс______________кН;

способ создания усилия________________________;

масштабы машинных диаграмм:

для нагрузок_____________кгс/см______________Н/см.

1.2. Геометрические характеристики образцов (ГОСТ 8817-58, 2055-43):

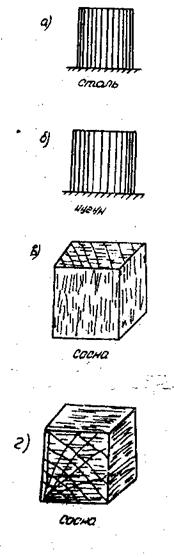а) стальной образец

диаметр d₀ = ________________cм;

высота h₀ = _________________см;

площадь поперечного сечения

А₀ = ___________________см²;

б) чугунный образец

диаметр d₀ = ________________cм;

высота h₀ = _________________см;

площадь поперечного сечения

А₀ = ___________________см²;

в) деревянный образец

(сжатие вдоль волокон)

размеры а = ________________см;

в = ________________см;

высота h₀ = ________________ см;

площадь поперечного сечения

А₀ = ___________________см²;

г) деревянный образец

(сжатие поперек волокон)

размеры а = ________________см;

в = ________________см;

высота h₀ = ________________ см;

площадь поперечного сечения

А₀ = ___________________см²

Рис.5.

Дерево является естественным композиционным материалом (КМ). В настоящее время широкое применение находят искусственные КМ: боро, - угле, - органо, - стеклопластики и им подобные материалы. Их отличительные особенности – высокая удельная прочность, немагнитность, коррозионная стойкость, легкость ремонта и т.п.

2. Результаты испытаний

2.1. Вид образцов после испытания

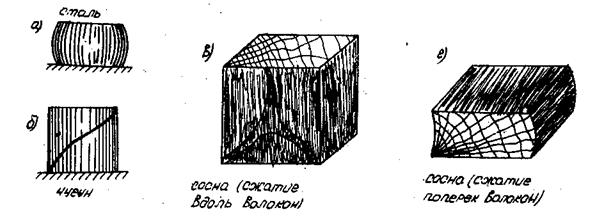
Рис.6.

2.2. Значения сжимающего усилия, напряжения и соответствующие им

деформации на различных стадиях нагружения образцов из пластич-

ных материалов.

2.2.1. Размеры и деформация стального образца при испытании:

высота образца на пределе текучести h_т = ____________см;

абсолютная деформация образца на пределе текучести

Δh_т = h₀ – h_т _______________= ________см;

относительная деформация ε_т = 100∙Δh_т / h₀ = ___________= _____%;

диаметр в конце испытания d_к =____________см:

площадь сечения в конце испытания

A_к = πd_к²/4 = _________________= _________см²;

высота в конце испытания h_к = ____________см;

абсолютная продольная деформация в конце испытания

Δh_к = h₀ – h_к _______________= ________см;

относительная деформация ε_к = 100∙Δh_к / h₀ = ___________= _____%;

усилие, соответствующее пределу текучести F_тс =____________кгс;

предел текучести при сжатии

σ_тс = F_тс /А₀ = _____________=_______кгс/см² =______МПа;

усилие в конце испытания F_кс =____________кгс;

напряжение в конце испытания

σ_кс = F_кс /А_к = _____________=_______кгс/см² =______МПа.

2.2.2. Размеры и деформация образца из дерева при испытании на сжатие

поперек волокон:

высота образца на пределе текучести h_т = ____________см;

абсолютная деформация образца на пределе текучести

Δh_т = h₀ – h_т _______________= ________см;

относительная деформация ε_т = 100∙Δh_т / h₀ = ___________= _____%;

размеры поперечного сечения в конце испытания:

а_к =__________см; b_к = ____________см;

площадь сечения в конце испытания

A_к = а_к ∙ b_к = _________________= _________см²;

высота в конце испытания h_к = ____________см;

абсолютная продольная деформация в конце испытания

Δh_к = h₀ – h_к _______________= ________см;

относительная деформация ε_к = 100∙Δh_к / h₀ = ___________= _____%;

усилие, соответствующее пределу текучести F_тс =____________кгс;

предел текучести при сжатии

σ_тс = F_тс /А₀ = _____________=_______кгс/см² =______МПа;

усилие в конце испытания F_кс =____________кгс;

напряжение в конце испытания

σ_кс = F_кс /А_к = _____________=_______кгс/см² =______МПа.

2.2.3. Напряжения и деформации для построения диаграмм сжатия:

Материал	σтс ,МПа	εт , %	σкс ,МПа	εк , %
Сталь
Дерево поперек волокон

2.3. Значения сжимающего усилия, напряжения и соответствующие им

деформации на различных стадиях нагружения образцов из хрупких

материалов.

2.3.1. Результаты испытания чугунного образца:

максимальное сжимающее усилие F_вс = __________кгс;

предел прочности или временное сопротивление сжатию

σ_вс = F_вс /A₀ =__________= _______кгс/см² =________МПа;

высота образца при разрушении h_к = __________см;

абсолютная продольная деформация при разрушении

Δh_к = h₀ – h_к =_______________= ________см;

относительная деформация ε_к = 100∙Δh_к / h₀ = ___________= _____%;

2.3.2. Результаты испытания дерева вдоль волокон:

максимальное сжимающее усилие F_вс = __________кгс;

предел прочности или временное сопротивление сжатию

σ_вс = F_вс /A₀ =__________= _______кг/см² = _______МПа;

высота образца при разрушении h_к = __________см;

абсолютная продольная деформация при разрушении

Δh_к = h₀ – h_к =_______________= ________см;

относительная деформация ε_к = 100∙Δh_к / h₀ = ___________= _____%;

2.3.3. Напряжения и деформации для построения диаграмм сжатия:

Материал	σвс , МПа	ε к , %
Чугун
Дерево вдоль волокон

2.4. Диаграммы напряжений испытанных материалов:

Рис. 7.

Нумерация диаграмм:

1 – сталь, 2 – дерево поперек волокон, 3 – чугун, 4 – дерево вдоль волокон

3. Выводы

3.1. Какие из данных материалов относятся к пластичным и хрупким,

изотропным и анизотропным, однородным и неоднородным?

3.2. Какие напряжения являются опасными для хрупких и пластичных

материалов?

3.3. Сопоставить удельную прочность σ_вс /γ чугуна и дерева вдоль волокон,

считая их удельные веса равными соответственно 7,7∙10^-2 МН/м³ и

0,54∙10^-2МН/м³.

Чугун - σ_вс /γ =________________= __________Па/Н/м³

Дерево - σ_вс /γ =________________= __________Па/Н/м³

Работу выполнил студент____________________

Оценка теоретических знаний____________________

Работу проверил____________________

«____»______________20 г.

Контрольные вопросы

1. Каково общее устройство испытательной машины?

2. Какие образцы применяются при испытании на растяжение и сжатие?

3. Какие материалы относятся к пластичным и хрупким?

4. Какие материалы являются изотропными и анизотропными?

5. Какие материалы называются однородными и неоднородными?

6. Каковы диаграммы сжатия стали и чугуна?

7. В чем различие диаграмм растяжения и сжатия стального образца?

8. Почему образец из стали при сжатии принимает бочкообразную форму и как можно уменьшить это явление?

9. Как формулируется гипотеза сплошности материала?

10. В каком напряженном состоянии находится материал сжатого образца?

11. На основании какого принципа тип захвата не оказывает существенного влияния на напряженное состояние точек образца, достаточно удаленных от места закреплении?

12. В каком сечении сжатого образца действуют наибольшие касательные напряжения?

13. В каких координатах вычерчивается машинная диаграмма?

14. Как ведут себя деревянные образцы при сжатии вдоль и поперек волокон?

15. Приблизительно с каким отношением высоты к диаметру должен быть выполнен стальной образец при испытании на сжатие?

16. По какой формуле определяются напряжения при испытании на сжатие?

17. Почему стальной образец при испытании на сжатие невозможно разрушить? Какое напряжение для него является опасным?

18. Сопоставить допускаемые напряжения на сжатие и растяжение для рассматриваемых материалов.

19. Что такое удельная прочность.

Лабораторная работа № 4

ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ

ПРИ КРУЧЕНИИ

Цель работы: экспериментально определить касательные напряжения и

угол закручивания вала и сопоставить их с соответствую-

щими теоретическими.

Задание для самостоятельной подготовки к работе

Изучить порядок расчета максимального напряжения и угла закручи-вания при кручении круглого вала.

Литература

1. Конспект лекций.

2. Ямпольский Е.Д. Сопротивление материалов, 1972.

3. Феодосьев В.И. Сопротивление материалов. М., 1970.

1. Подготовка к испытаниям

1.1. Схема установки.

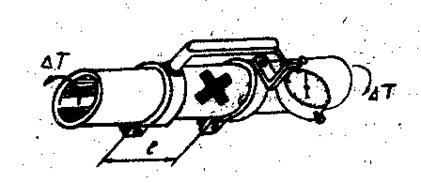
Рис. 14.

l – расстояние между закрепленными на валу кольцами ( рабочая

длина);

ΔТ – крутящий момент.

1.2. Перемещения при закручивании участка вала на рабочей длине.

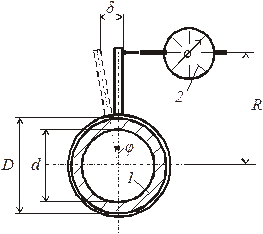
φ – угол закручивания на рабочей длине;

δ – разность перемещений концов консо-

лей, укрепленных на кольцах;

1 – сечение вала;

2 – индикатор часового типа для замера

перемещения δ.

Рис. 15.

1.3. Характеристики торсиометра:

расстояние от оси вала до ножки индикатора R = _____________ см;

рабочая длина вала l = ____________________ cм;

цена деления индикатора С = ________________ мм;

цена деления тензоизмерителя С₁ = ______________.

1.4. Характеристики материала исследуемого вала:

материал вала ________________________;

модуль упругости при растяжении Е = _______кгс/см² = _______МПа;

коэффициент Пуассона μ = ________________;

модуль упругости при сдвиге G = ____________ = ________ кгс/cм².

2. Определение теоретических значений

максимального напряжения и угла закручивания

2.1. Определение максимального напряжения.

2.1.1. Геометрические характеристики сечения вала:

наружный диаметр D = _______________cм;

внутренний диаметр d = _______________ cм;

отношение диаметров α = d/D = ________________

полярный момент инерции I_p = ______________ = ___________ =

= ________см⁴;

полярный момент сопротивления W_р = ____________ = _________=

= _________cм³.

2.1.2. Максимальное касательное напряжение в сечении:

τ_max = ____________ = ___________ = _______кгс/см² = ________МПа.

2.1.3. Распределение касательных напряжений в сечении:

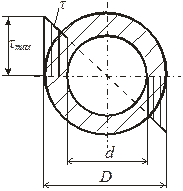
Рис. 16.

2.2. Угол закручивания φ на рабочей длине вала l:

φ = ________________= ______________=_________ рад = _______град;

2.3. Относительный угол закручивания:

θ =____________ = ____________ = ___________ град/м.

3. Определение напряжения и угла закручивания опытным путем

3.1. Журнал наблюдений

№№ ступ. нагр.	Крут. мо- мент Т, кгс∙см	Ступ. нагр. ΔТ, кгс∙см	Показания индикатора	Показания измерителя деформаций
λ	Δλ	λ1	Δλ1	λ3	Δλ3
Средняя ΔТср =	Δλср =	Δλ1ср =	Δλ3ср =

3.2. Обработка результатов наблюдений.

3.2.1. Определение напряжений:

деформации в главных направлениях:

ε₁ = Δλ_1ср∙С₁ = _____________= _____________ ;

ε₃ = Δλ_3ср∙С₁ = _____________= _____________ .

главные напряжения:

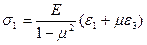= _______________________ = ___________кгс/см² =

= _______________МПа;

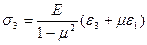= _______________________ = ___________кгс/см² =

= _______________МПа.

максимальное касательное напряжение:

τ_max = (σ₁ - σ₃)/2 = ______________ = ______ кгс/см² = _______МПа.

3.2.2. Определение угла закручивания:

φ = Δλ_ср∙С/R = _______________ = ___________рад = ________град.

4. Выводы

4.1. Сопоставление теоретических и опытных данных

Сравниваемые данные	Теоретическое значение	Опытное значение	Расхождение, %
Напряжение, τmax
Угол закручива- ния, φ

4.2. Напряженное состояние исследованной точки вала:

________________________________________________________________

Работу выполнил студент____________________

Оценка теоретических знаний____________________

Работу проверил____________________

«____»______________20 г.

Контрольные вопросы

1. В чем состоит суть гипотезы плоских сечений при кручении брусьев круглого поперечного сечения?

2. Какой вид имеет закон Гука при кручении?

3. По какой формуле определяют касательные напряжения в произво-льной точке сечения вала?

4. По какой формуле определяются полярные моменты инерции сплошного и кольцевого сечений вала?

5. Какие сечения при кручении наиболее экономичны? Почему?

6. Какие точки сечения вала при кручении являются наиболее нагруженными?

7. Как формулируется и записывается условие прочности при круче-нии вала?

8. Почему при равных площадях полярный момент инерции кольце-вого сечения больше, чем сплошного?

9. Как формулируется и записывается условие жесткости при кру-чении?

10. Как выражается связь между упругими постоянными материала?

11. Какое различие наблюдается при разрушении кручением валов из хрупкого и пластичного материала? Как это объяснить?

12. Что называют жесткостью при кручении? Какова её размерность?

13. Модуль упругости стали в два раза больше, чем меди. Какое различие в углах закручивания и напряжениях двух одинаковых по размеру валов из этих материалов?

14. Объясните устройство торсиометра Бояршинова.

15. Как ориентированы и чему равны главные напряжения при круче-нии вала?

16. Из каких соображений определяется величина ступени нагружения и их количество?

17. Каково влияние рабочей длины торсиометра на показания индика-тора при определении угла закручивания?

Лабораторная работа №5

ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ

ПРИ ИЗГИБЕ БАЛКИ

Цель работы: 1. Экспериментально определить нормальные напряжения и

перемещения при изгибе балки и сопоставить их с соот-

ветствующими теоретическими значениями.

2. Ознакомиться с работой тензодатчиков и индикаторов ча-

сового типа.

Задание для самостоятельной подготовки к работе

Изучить порядок определения внутренних усилий, нормальных и касательных напряжений, перемещений при изгибе.

Литература

1. Конспект лекций.

2. Ямпольский Е.Д. Сопротивление материалов, 1972.

3. Феодосьев В.И. Сопротивление материалов. М., 1970.

1. Подготовка к испытаниям

1.1. Общий вид испытательной установки с измерительными приборами и

определяемые в работе перемещения.

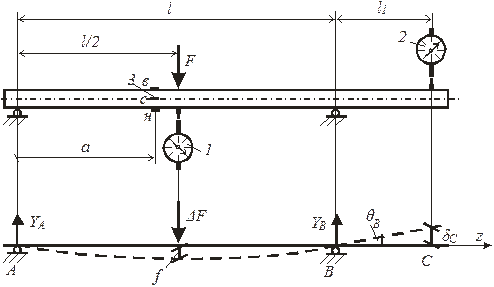
Рис.11.

1 – индикатор часового типа для определения прогиба под силой;

2 – индикатор часового типа для определения перемещения точки С;

3 – расположение тензодатчиков для определения деформации верх-

него, среднего и нижнего волокон балки;

f – прогиб под силой;

δ_С – перемещение сечения С консольной части балки;

θ_В – угол поворота сечения над опорой В.

1.2. Характеристики испытательных установок на различных рабочих

местах (РМ).

Характеристики установок	РМ №1	РМ №2	РМ №3
Длина пролета l , см Расстояние а от левой опоры до сечения, где установлены тензодатчики, см Расстояние L от прибора Мартенса до се- чения, где определяется угол поворота, см Длина консольной части балки l1 , см Сечение балки высота сечения h, см ширина сечения в, см толщина стенки двутавра d, см Материал балки Ступень нагружения, кгс	- 2,2 1,1 - сталь	дв.№12 6,4 0,73 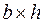сталь	- 1,8 0,8 - сталь

1.3. Измерительные приборы и их характеристики.

Рис. 13. Схема тензодатчика

Рис. 12. Индикатор часового типа

Цена деления шкалы тензоизмерителя С₁ =__________________

Цена деления индикатора часового типа С₂ = 0,01мм.

2. Определение теоретических значений напряжений и перемещений

2.1. Определение напряжений.

2.1.1. Геометрические характеристики сечения балки:

момент инерции сечения I_x =_____________________________см⁴;

момент сопротивления W_x = ______________________________см³;

2.1.2. Внешние и внутренние уилия:

ступень нагружения ΔF = _______________кгс;

реакции опор Y_A = Y_B = _________________кгс;

изгибающий момент в сечении с координатой а:

M(a) = ___________=__________________=________кгс∙см.

2.1.3. Нормальные напряжения в исследуемом сечении:

верхние волокна: σ_вт =_____=__________=_____кгс/см² = _____МПа;

нижние волокна: σ_нт =_____=__________=_____кгс/см² = _____МПа;

средние волокна: σ_ст =_____=__________=_____кгс/см² = _____МПа;

2.1.4. Эпюра распределения нормального напряжения по высоте сечения:

_______________________________________________

________________________________________________

2.2. Определение теоретических значений перемещений

2.2.1. Прогиб посредине пролета

f_т = _____________ = ____________________= ______см =______мм;

2.2.2.Угол поворота опорного сечения

θ_Вт = ______________=_____________________= ___________рад.

3. Результаты испытаний

3.1. Журнал наблюдений деформаций по тензометрам

№№ ступ. нагр.	Наг- рузка F,кгс	Cту- пень ΔF, кгс	Отсчеты по тензометрам
верх. волокна	нижн. волокна	средн.волокна
отсчет λ	разность Δλ	отсчет λ	разность Δλ	отсчет λ	разность Δλ
Среднее ΔF = ______	Средн. Δλв = _______	Средн. Δλн = ________	Средн. Δλс = ________

3.2. Журнал наблюдения перемещений по индикаторам

№№ ступ. нагр.	Нагрузка F , кгс	Ступень нагруж., ΔFi , кгс	Отсчеты по индикаторам
индикатор 1	индикатор 2
отсчет λ1	разность отсчетов Δλ1	отсчет λ2	разность отсчетов Δλ2
Среднее значение ΔF = ______кгс	Средняя разность Δλ1 =_______	Средняя разность Δλ2 =_______

3.3. Обработка результатов наблюдений

3.3.1.Относительные деформации волокон:

верхние: ε_в = Δλ_в∙С₁ = ___________________ = ______________

нижние: ε_н = Δλ_н∙С₁ = ___________________ = ______________

средние: ε_с = Δλ_с∙С₁ = ___________________ = ______________

3.3.2.Экспериментальные значения напряжений в волокнах:

верхние: σ_вэ = Е∙ε_в = _______________ = _______кг/см² _______МПа;

нижние: σ_нэ = Е∙ε_н = _______________ = _______кг/см² _______МПа;

средние: σ_сэ = Е∙ε_с = _______________ = _______кг/см² _______МПа.

3.3.3. Экспериментальные значения перемещений:

стрела прогиба f_э = Δλ₁∙C₂ = ____________ =__________мм;

перемещение точки С δ_С = Δλ₂∙С₂ = ______________= ________мм;

угол поворота сечения над опорой:

θ_Вэ = δ_C/l₁ = _________________ = _________ рад.

4. Выводы

Сравнение теоретических данных с опытными

Сравниваемые величины	Теоретическое значение	Опытное значение	Расхождение, %
Нормальное напряжение σв , МПа
Прогиб f , мм
Угол поворота θВ , рад.

Работу выполнил студент____________________

Оценка теоретических знаний____________________

Работу проверил____________________

«____»______________20 г.

Контрольные вопросы

1. Какой изгиб называется поперечным, плоским, чистым?

2. Чему равны поперечная сила и изгибающий момент в поперечном сечении балки?

3. Сформулировать правило знаков для поперечной силы и изгибаю-щего момента.

4. По каким формулам определяются нормальные напряжения в лю-бой точке сечения балки и максимальные напряжения?

5. По каким формулам вычисляют моменты сопротивления для прямо-угольного сечения?

6. По каким формулам определяют осевые моменты инерции круглого и прямоугольного сечений?

7. По какой формуле определяют касательные напряжения при изгибе?

8. Какой вид напряженного состояния испытывают верхние и нижние волокна балки при изгибе?

9. Как определяется статический момент отсеченной части сечения балки при вычислении касательного напряжения в какой-либо точке сечения по формуле Журавского?

10. В каком напряженном состоянии находится материал нейтрального слоя балки при поперечном изгибе?

11. Что называется жесткостью при изгибе? Какой вид имеет закон Гука при изгибе?

12. Как записывается дифференциальное уравнение оси изогнутой балки?

13. Что представляют собой граничные условия для балки, шарнирно опертой по концам?

14. По какому закону изменяются нормальные напряжения в попереч-ном сечении балки при изгибе?

15. В каком месте исследуемой в лабораторной работе балки угол поворота поперечного сечения балки равен нулю?

16. Каким прибором измеряют прогиб балки? Как он устроен?

17. Каким образом измеряют угол поворота сечения балки?

18. Какие показания дает тензометр, установленный на уровне центров тяжести сечения? Как объяснить эти показания?

19. Как вычислить напряжение по экспериментально найденной деформации?

20. Как и почему изменятся напряжения и перемещения исследуемой в лабораторной работе балки, если развернуть её на 90° и положить на опоры плашмя?

Лабораторная работа № 6

ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ ТОЧКИ

ПОВЕРХНОСТИ ВАЛА ПРИ ИЗГИБЕ С КРУЧЕНИЕМ

Цель работы: 1. Ознакомиться с основами электрического тензометрирова-

ния для определении напряжений при сложном сопротив-

лени.

2. Проверить справедливость теоретических формул опреде-

ления главных напряжений при совместном действии

изгиба и кручения.

Задание для самостоятельной подготовки к работе

Знать основные определения и формулы расчета главных напряжений и положения главных площадок при изгибе с кручением.

Литература

1. Конспект лекций.

2. Ямпольский Е.Д. Сопротивление материалов, 1972.

3. Феодосьев В.И. Сопротивление материалов. М., 1970.

1. Подготовка к испытаниям

1.1. Схема установки:

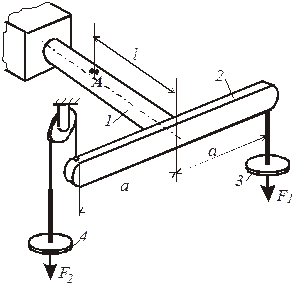
1 - консольно закрепленный вал ко-

льцевого сечения;

2 – рычаг, закрепленный на конце

вала;

3 и 4 – грузы;

А – точка на поверхности вала с нак-

леенными тензодатчиками.

Рис. 17.

1.2. Размеры установки:

расстояние от конца консоли до исследуемой точки l = 40см;

плечо рычага а = 30см;

наружный диаметр вала D = 4,5cм;

внутренний диаметр вала d = 4cм;

отношение диаметров α = d/D = 0,889.

1.3. Характеристики материала вала:

материал – диралюминий;

модуль упругости при растяжении Е = 0,7∙10⁶кгс/см² = 0,7∙10⁵МПа;

коэффициент Пуассона μ = 0,34.

2. Определение теоретических значений главных напряжений и положения

главных площадок

2.1. Схема нагружения балки и эпюры изгибающих и крутящих моментов:

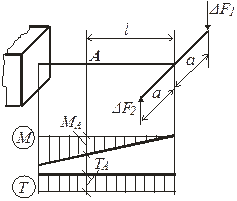
Рис. 18.

2.2.Значение внешних и внутренних сил:

ступени нагружения: ΔF₁ = _______кгс; ΔF₂ = ________кгс;

изгибающий момент в сечении А:

М_А = (ΔF₁ – ΔF₂)l = ____________= _________кгс∙см;

крутящий момент:

Т = (ΔF₁ + ΔF₂)a = ____________ = __________кгс∙см.

2.3.Моменты сопротивления сечения:

осевой W_x = πD³(1 – α⁴)/32 = __________________= ________см³;

полярный W_p = 2W_x = ____________= ___________см³.

2.4. Нормальное и касательное напряжения в исследуемой точке:

σ = М_А / W_x = __________ = _________кгс/см² = __________МПа;

τ = - T /W_p = ____________ = _________кгс/см² = __________Мпа.

2.5. Напряженное состояние точки А:

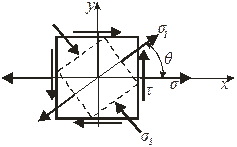
Рис.19.

2.6.Главные напряжения и положение главных площадок:

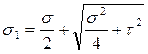= ____________________ = _______кгс/см² =_____Мпа;

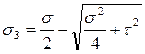= ____________________ = _______кгс/см²