Вдали от излучателя

По определению векторного потенциала

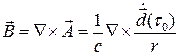
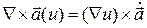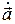Воспользуемся формулой , где - производная по скаляру u. При дифференцировании по координате 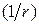можно считать константой (т.к. получим величину 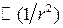). Тогда находим

( )

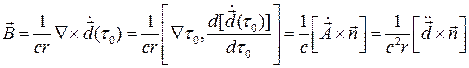Здесь и всюду в этом параграфе .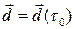

Так как для любого 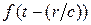имеем 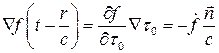поскольку .

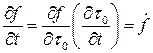Следовательно

( )

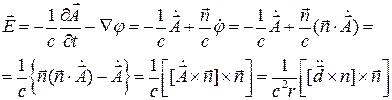Из ( ), ( ) видим, что

( )

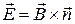Напряжение электрического и магнитного полей зависят от координат по закону

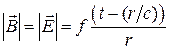
т.е. амплитуда волны уменьшается по закону 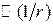в то время как в электростатике: 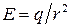. При этом векторы 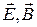и 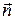взаимно перпендикулярны. Область вдали от излучателя, в которой электромагнитном поля описывается сферическими волнами носит название волновой зоны.

Рассмотрим пространственное распределение поля ( ) относительно вектора 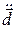. Направим вдоль него ось z сферической системе координат 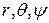, где 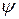- азимут. угол:

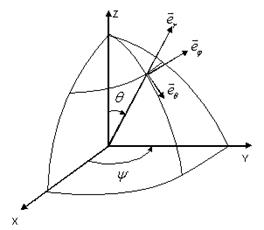
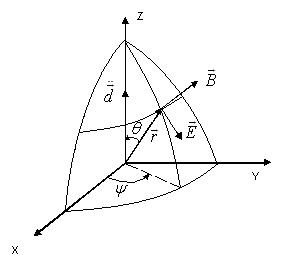
Их формул ( ), ( ) видим, что векторы 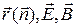параллельны, соответственно, базисным векторам 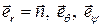сферической системы координат. Поэтому имеем

( )

( )

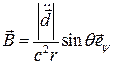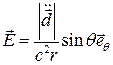С помощью ( ), ( ) находим плотность потока энергии

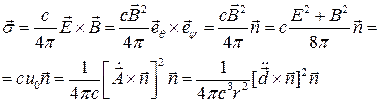
По модулю 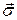равен

( )

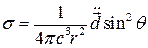Видим, что напряженность поля E и B и плотность потока энергии имеют максимальное значения в плотности 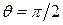(экваториальная плотность). То, что 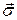отличен от нуля и всегда направлен от излучающей системы имеет простой смысл: имеется поток электромагнитной энергии, направленный от системы в окружающее пространство. Это и оправдывает термины “поле излечения”, “излучатель”.

Найдем мощность, излученную в телесный угол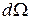

( )

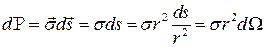
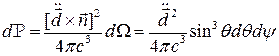Полная мощность, излучаемая системой (полная)

( )

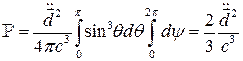Таким образом 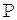определяется только величиной 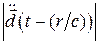и не зависит от расстояния до излучателя, как и следует ожидать на основании закона сохранения энергии.