Аппроксимация источникового члена
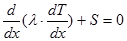
Прежде чем перейти к определению основных правил, рассмотрим источниковый член S уравнения стационарной задачи теплопроводности. Часто источниковый член является функцией самой зависимой переменной Т и тогда желательно учесть эту зависимость при построении дискретного аналога. Однако формально можем учитывать только линейную зависимость, так как решение дискретных уравнений будет осуществляться, как увидим позже, с помощью методов решения систем линейных алгебраических уравнений. Способ линеаризации зависимости S от Т обсуждается далее. Здесь нам достаточно записать среднее значение S в виде
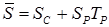 ,
,
где 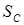 представляет собой постоянную составляющую S, a
представляет собой постоянную составляющую S, a 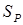 — коэффициент (очевидно, что
— коэффициент (очевидно, что 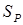 не есть значение S в точке Р).
не есть значение S в точке Р).
Наличие 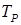 в выражении отражает тот факт, что при записи среднего значения
в выражении отражает тот факт, что при записи среднего значения 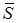 мы предполагали, что значение
мы предполагали, что значение 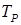 распространяется на весь контрольный объем, другими словами, использовался ступенчатый профиль (следует заметить, что можно использовать ступенчатый профиль для S и кусочно-линейный для члена dT/dx).
распространяется на весь контрольный объем, другими словами, использовался ступенчатый профиль (следует заметить, что можно использовать ступенчатый профиль для S и кусочно-линейный для члена dT/dx).
Дискретный аналог уравнения теплопроводности с линеаризованным источниковым членом будет иметь такой же вид (5.1), но с другими выражениями для коэффициентов
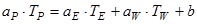 (5.1)
(5.1)
где 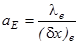 ,
, 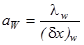 ,
, 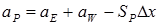 ,
, 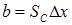 (5.2)
(5.2)
Теперь можно сформулировать основные правела, которым должны подчиняться дискретные аналоги уравнений для обеспечения физичности решения н сохранения полного баланса.
