Ангармонический осциллятор

Если в выражении для восстанавливающей силы (см. рис. 2) учесть член второй степени в х, то уравнение движения принимает вид

х¹¹ + ω₀²х = αх² (90)

Это линейное уравнение называется уравнением ангармонического (нелинейного) осциллятора. Его можно решать методом разложения по малому параметру, каковым может быть начальное смещение или начальная скорость. Решение ищем в виде х = х₁ + х₂, где х₁ и х₂ находим из уравнений

х₁ ¹¹ + ω₀²х₁ = 0, х₂ ¹¹ + ω₀²х₂ = αх₁ ².

Решением первого уравнения при нулевой начальной скорости и начальном смещении a будет функция x₁ = a cos ω₀t, в которой величину a будем считать малым параметром. Подставляя x₁ во второе уравнение, решаем получившееся неоднородное уравнение для функции x₂ (t), которая уточняет решение x₁ (t) появлением колебания удвоенной частоты 2 ω₀.

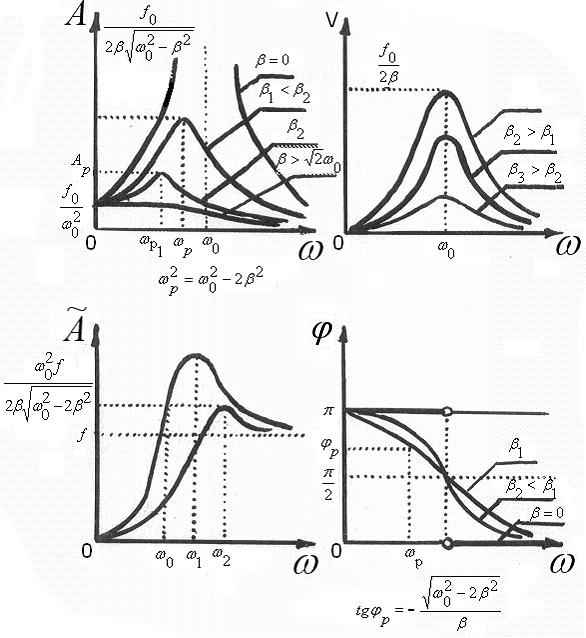
Рис. 22. Резонансные кривые для резонанса смещений, скоростей и ускорений. Фазовые соотношения

Модулированные колебания

Если на осциллятор воздействует негармоническая периодическая сила, то, разложив ее в ряд Фурье, определяем реакцию осциллятора на каждую Фурье-компоненту (гармонику), а затем производим сложение всех полученных реакций. В результате

x(t) = 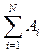cos(ω_i t - j_I ). (91)

Это допустимо в силу линейности исходного дифференциального уравнения колебаний.

Сигнал, поступающий на осциллятор, может быть промодулирован по амплитуде, т.е. вынуждающее воздействие имеет вид

x = А cos(ωt - j),

где, в свою очередь, амплитуда А изменяется также по гармоническому закону, но с меньшей частотойn:

А = а(1 + к cosn t). (92)

Данное сложное колебание разложимо на три гармоники с центральной несущей частотой ω, и с боковыми суммарной ω + n,и разностной ω - n частотами, причем амплитуды боковых частот одинаковы. Множитель к – параметр, характеризующий глубину модуляции, на амплитуду несущей гармоники не влияет. В результате усиления этих трех компонент при их взаимодействии с осциллятором изменяются их амплитуды и фазы. В результате на выходе мы будем иметь искаженный суммарный сигнал. Степень искажения модулированного сигнала после усиления тем больше, чем острее резонансная кривая осциллятора. Таким образом, мы имеем техническое противоречие: для получения больших коэффициентов усиления необходима острая резонансная кривая, а для минимальных искажений сигнала в процессе усиления необходимо сохранение пропорций хотя бы между амплитудами, т.е. широкая резонансная кривая с мальм усилением. На практике ищется компромисс между этими требованиями.

Дальнейший анализ данной задачи такой же, как и для гармонического воздействия на осциллятор.

Рассмотренная задача замечательна еще в одном отношении. В ней рассмотрены колебания, которые совершаются не по гармоническому закону. Однако, если фаза меняется гораздо быстрее, чем амплитуда, то они будут «почти гармоническими». Обобщая, любое выражение вида x(t) = A(ω₁t) cos (ω₂t) , где ω₁ << ω₂ , может рассматриваться как приблизительно гармоническое. Можно дать еще одно определение амплитуды негармонических колебаний: амплитуда – это выражение, стоящее перед гармонической функцией и медленно меняющееся со временем по сравнению с фазой.