Расчет коэффициента усиления регулятора

Введение

Курсовая работа по дисциплине «Теория автоматического управления» предполагает изучение составляющих дисциплины и приобретение навыков расчета параметров элементов систем автоматического управления (САУ) и анализа их характеристик. Данная работа предусматривает возможность практического применения знаний, полученных на лекциях, лабораторных работах и в процессе самостоятельной подготовки. При выполнении курсовой работы необходимо решить ряд задач, тематика которых отражает основные разделы изучаемой дисциплины.

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Задание на курсовую работу

Параметры исходной САУ

a1	0,08	b2	0,018	c1		d2	0,009	g	1,2 … 7
a0		b1	0,13	c0		d1	0,825	z	-10

Система автоматического управления представлена структурной схемой, показанной на рис. 1

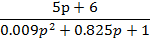2 niVkAzEeoVmuZcBlVlIjm8P4xXCWRzaemyrJgUnVy1i0Mgd6IiM9N6EruzSOyZH2EqpbJMxBv7x4 bCg04D5R0uLiFtR/3DInKFEvDZJ+PppO46YnZTo7G6PiTi3lqYUZjlAFDZT04iqk64h1G7jE4dQy 8Ran2FdyqBkXMjF/OJ648ad68vp14sufAAAA//8DAFBLAwQUAAYACAAAACEA/LL6Ut0AAAAKAQAA DwAAAGRycy9kb3ducmV2LnhtbEyPwW6DMAyG75P2DpEn7TKtYahAoYRqm7Rp13Z9gEBcQCUOImmh bz/vtJ1sy59+fy53ix3EFSffO1LwsopAIDXO9NQqOH5/PG9A+KDJ6MERKrihh111f1fqwriZ9ng9 hFZwCPlCK+hCGAspfdOh1X7lRiTendxkdeBxaqWZ9MzhdpBxFKXS6p74QqdHfO+wOR8uVsHpa35K 8rn+DMdsv07fdJ/V7qbU48PyugURcAl/MPzqszpU7FS7CxkvBgXxJs4ZVbBOuDKQRBk3NZNxmoOs Svn/heoHAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAA AFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAA AAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAWG5L7zkCAAAqBAAADgAAAAAAAAAA AAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEA/LL6Ut0AAAAKAQAADwAAAAAA AAAAAAAAAACTBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAJ0FAAAAAA== " stroked="f">

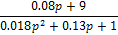K

Рис. 1. Структурная схема САУ.

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Статическая ошибка = 2,5 %

Расчет коэффициента усиления регулятора

Запишем уравнения для нахождения коэффициентов передачи системы автоматического управления (рис.1) в статическом режиме, статический режим характеризуется тем, что в нем все производные равны нулю (p=0).

Коэффициент передачи по задающему воздействию.

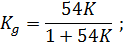
Коэффициент передачи по возмущающему воздействию.

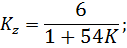
Составим передаточную функцию данной САУ, используя принцип суперпозиции.

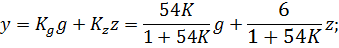
Наибольшее отклонение выходного сигнала достигается при g_min=1.2 и z_max= =-10

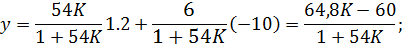
Заданная максимальная допустимая ошибка 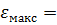2.5%, найдем значение выходной переменной для заданной статической ошибки;

Приравняем два выражения для выходной переменной и найдем коэффициент К при максимальной статической ошибке.

.

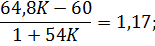
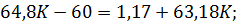
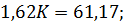
Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Изм.

Лист

№ докум.

Лист

БГТУ. БГТУ. 210100. 12. 000. ПЗ

2. Расчет и построение внешних статических характеристик САУ

Внешняя статическая характеристика отражает изменение выходного параметра САУ при изменении возмущающего воздействия для заданного постоянного значения задающего воздействия. Несколько характеристик, построенных для различных значений задания g, образуют семейство внешних статических характеристик.

Подставим в передаточную функцию нашей САУ найденное в 1 пункте работы значение коэффициента усиления К:

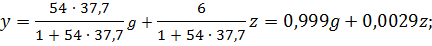
Возьмем минимальное, максимальное и среднее значения g и рассчитаем для каждого из значений по 2 точки функции при изменении z для построения внешних статических характеристик, которые являются прямыми.

Для g_min=1.2

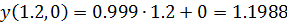
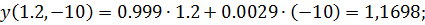
Для g_ср=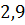

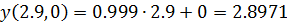
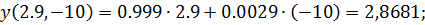
Для g_max=7

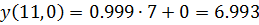
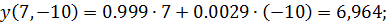
Изм.

Лист

№ докум.

Лист

БГТУ. БГТУ. 210100. 12. 000. ПЗ

Занесем вычисленные данные в таблицу:

z g		-10
1.2	1,1988	1,1698
2.9	2,8971	2,8681
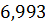		6,964

Рассчитаем статические ошибки

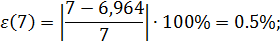
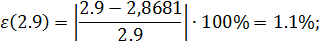
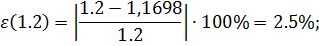
Внешние статические характеристики представлены на рис. 2.

Y

1.2

Изм.

Лист

№ докум.

Лист

БГТУ. БГТУ. 210100. 12. 000. ПЗ

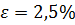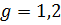1.1988

1.1698

Y

2.9

2.8971

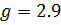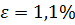2.8681

Y

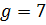6.993

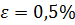6.964

Рис. 2. Внешние статические характеристики.

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

3. Определение передаточной функции САУ, расчёт корней характеристического уравнения

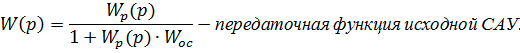
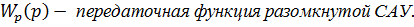
Так как обратная связь единична, то 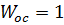, значит

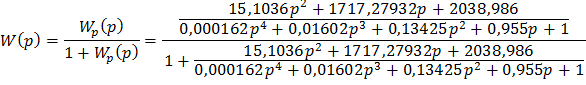
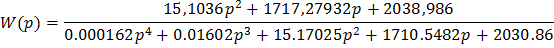
Знаменатель передаточной функции - это характеристический полином системы:

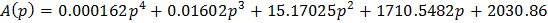
Для определения корней этого уравнения воспользуемся программным комплексом MathCAD (рис. 3).

Рис. 3. Расчет корней характеристического уравнения в MathCAD.

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Получены корни характеристического уравнения

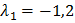
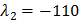
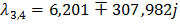
Комплексно-сопряжённые корни с положительной вещественной частью определяют наличие в системе нарастающих гармонических колебаний с частотой колебаний 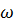=307.982 рад/с, периодом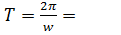 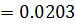, коэффициентом расхождения 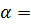6.201, декрементом расхождения 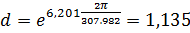, что говорит о неустойчивости данной САУ.

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

37.7

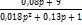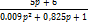g

y

z

4. Расчет и построение частотных характеристик эквивалентной разомкнутой САУ: АФЧХ, ЛАЧХ и ЛФЧХ.

Рис.4. Графическое изображение разомкнутой САУ

Передаточная функция разомкнутой САУ имеет следующий вид:

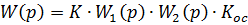
Примем 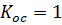, тогда

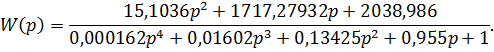
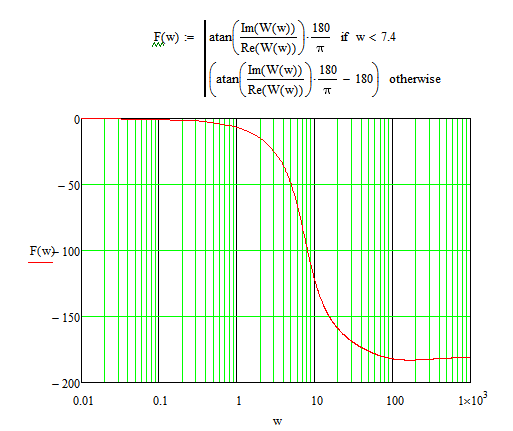
Введём замену p=jw и получим АФЧХ,

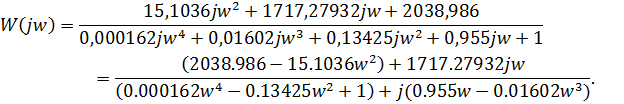
Построим с помощью пакета MatLab логарифмические амплитудную частотную характеристику (ЛАЧХ), фазо-частотную характеристику (ЛФЧХ) и амплитудную фазово-частотную характеристику (АФЧХ) для разомкнутой системы.Структурная схема разомкнутой САУ в среде MatLab представлена на рис.5.

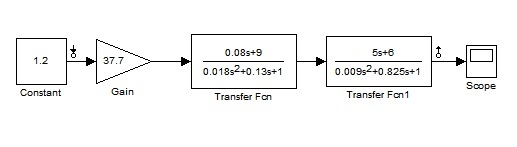
Рис.5. Модель разомкнутой САУ в MatLab Simulink

Логарифмические частотные характеристики определяют усилительные свойства системы (ЛАЧХ) и сдвиг фазы выходной величины (ЛФЧХ) в логарифмическом масштабе.

ЛАЧХ – модуль комплексной функции АФЧХ с учетом логарифмического масштаба, а ЛФЧХ – аргумент комплексной функции.

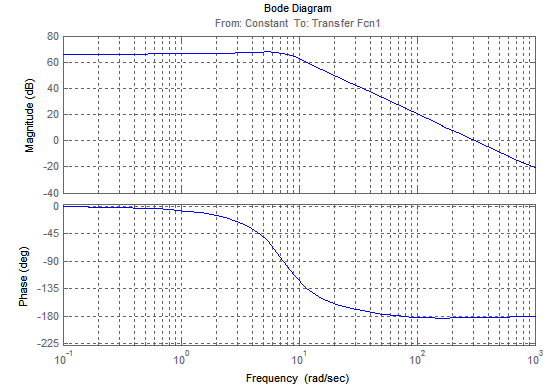
Построим с помощью пакета MatLab логарифмические амплитудную частотную характеристику (ЛАЧХ), фазово-частотную характеристику (ЛФЧХ) и амплитудную фазово-частотную характеристику (АФЧХ) для разомкнутой системы.

дубль и ссылки на рисунки нужны.

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Рис.6. ЛАЧХ и ЛФЧХ исходной САУ

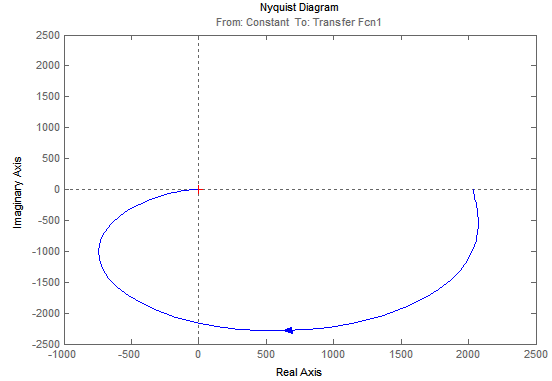
Рис.7. АФЧХ исходной САУ

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Для проверки построим все графики в MathCad

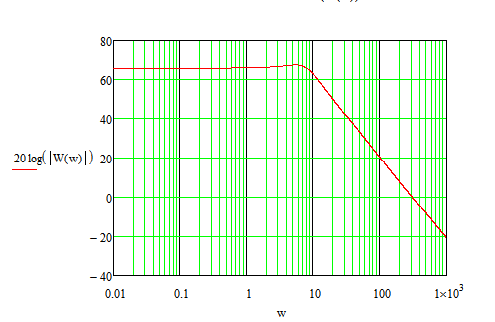
Рис.8. График ЛАЧХ разомкнутой САУ в MathCad

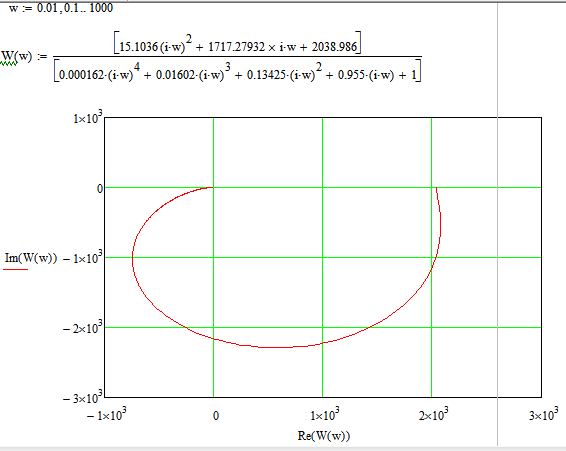
Рис.9. График АФЧХ разомкнутой САУ в MathCad

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Рис.10. График ЛФЧХ разомкнутой САУ в MathCad

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

5. Проверка на устойчивость исходной САУ по критерию Гурвица и Найквиста

Из пункта 3 характеристический полином:

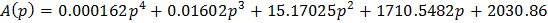
Для того, что бы составить определитель Гурвица надо по диагонали от левого верхнего до правого нижнего элемента матрицы выписать все коэффициенты. Пустые строки заполняем так, что бы чередовались строки с нечетными и четными индексами и когда коэффициент отсутствует на его месте пишем 0. Строим определитель Гурвица:

По определению САУ устойчива, если определитель Гурвица и все его диагональные миноры положительны:

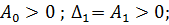
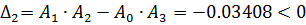
Отсюда следует, что САУ является неустойчивой.

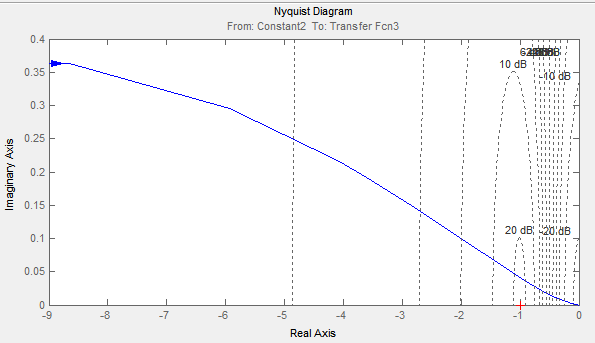
Проверим систему на устойчивость с помощью частотного критерия Найквиста. Для этого возьмем АФЧХ разомкнутой системы, которая была построена ранее (рис. 11).

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Рис.11. АФЧХ в окрестности точке (-1;0)

Формулировка критерия устойчивости по Найквисту: «Если разомкнутая система устойчива, то для устойчивости соответствующей замкнутой системы, необходимо, чтобы АФЧХ разомкнутой цепи не охватывало точку [-1;0] на комплексной плоскости».

Согласно критерию Найквиста, система не устойчива.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

6.Моделирование переходных характеристик исходной САУ

При отсутствии возмущений для граничных значений g. Структурная схема для моделирования в MatLab представлена на рис.12.

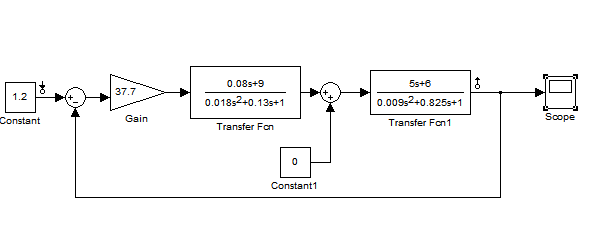
Рис.12. Схема исходной САУ в MatLab

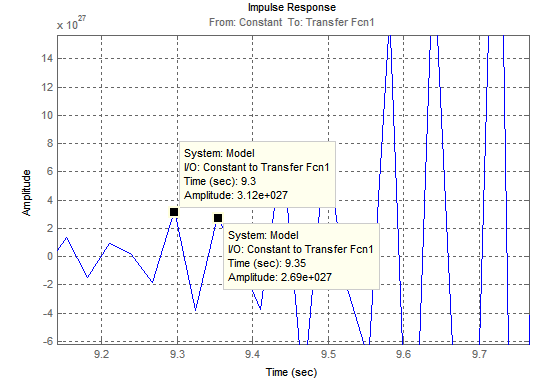
1) Здесь g не изменяется и равно своему минимальному значению 1,2 , возмущающее воздействие z тоже равно своему минимальному значению 0. Результат моделирования представлен на рис.12.

S pMvpfJJMArIGXx901EiHYlayyels7D9fzjJPxgtdBtsxqQYbO1H6yI4nZKDG9UUf1hFfhGrPXQHl HgkzMKgXXxsaNZjPlHSo3JzaT1tmBCXqlUbS53GaeqkHJ51cJOiY80hxHmGaI1ROHSWDuXLhefjG NVzhcioZiHvs5Ng0KjLweXw9XvLnfsh6fOPLXwAAAP//AwBQSwMEFAAGAAgAAAAhABHxqxvgAAAA CwEAAA8AAABkcnMvZG93bnJldi54bWxMj8FOg0AQhu8mvsNmTLwYu7RAaZGlURON19Y+wMBugcjO EnZb6Ns7nuxxZr788/3Fbra9uJjRd44ULBcRCEO10x01Co7fH88bED4gaewdGQVX42FX3t8VmGs3 0d5cDqERHEI+RwVtCEMupa9bY9Ev3GCIbyc3Wgw8jo3UI04cbnu5iqK1tNgRf2hxMO+tqX8OZ6vg 9DU9pdup+gzHbJ+s37DLKndV6vFhfn0BEcwc/mH402d1KNmpcmfSXvQK0jhNGVWQJJsVCCbSLFqC qHizjWOQZSFvO5S/AAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAA AAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsA AAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAGkB/JQ9AgAAKwQAAA4A AAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhABHxqxvgAAAACwEA AA8AAAAAAAAAAAAAAAAAlwQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAACkBQAAAAA= " stroked="f">

T

Рис.13. Переходная характеристика САУ при отсутствии возмущений

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

Как видим, система характеризуется колебаниями с нарастающей амплитудой, что свидетельствует о неустойчивости данной САУ.

Рассчитаем логарифмический декремент затухания, для этого возьмем на графике два амплитудных значения через один период

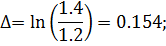
Период колебаний: T=t2-t1=9.85-9.83=0.02c

Частота: 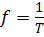=50 Гц, циклическая частота 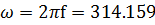рад/с.

Экспериментально полученные частота, период колебаний и логарифмический декремент расхождения совпадают с рассчитанными в 3 пункте, значит, расчет и моделирование выполнены верно.

Как видим, частота ( 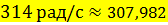рад/с) и декремент расхождения ( 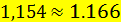) имеют погрешность менее 1% с ранее рассчитанными по п. 3, тем самым мы доказали правильность выполнения расчетов.

дубль

Добавить.

Поскольку система неустойчива её поведение мало зависит от возм и зад воздействий, поэтому построение дополнительных переходных характеристик лишено смысла.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

7. Синтез корректирующего устройства, обеспечивающего настройку исходной системы на технический оптимум.

Для достижения оптимальных показателей качества САУ необходимо настроить её на симметричный оптимум.

Желаемая передаточная функция разомкнутой системы, настроенной на симметричный оптимум, имеет вид:

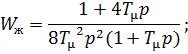
Где 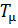- наименьшая постоянная времени нескорректированной системы.

Для определения 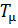запишем передаточную функцию разомкнутой нескорректированной системы

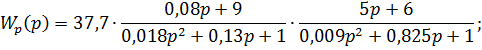
Рассчитаем корни полинома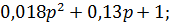

p₁=-3,6111+6,5204i;

p₂=-3,6111-6,5204i ;

Рассчитаем корни полинома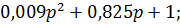

p₁=-90,4381 p₂=-1,2286;

найдём соответствующие им постоянные времени

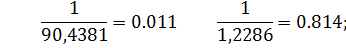
Запишем передаточную функцию САУ, разложив полином 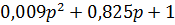на множители

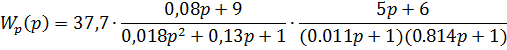
Наименьшая постоянная времени данной системы .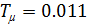

Желаемая передаточная функция системы имеет вид:

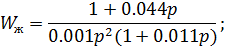
Рассчитаем передаточную функцию корректирующего устройства

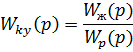
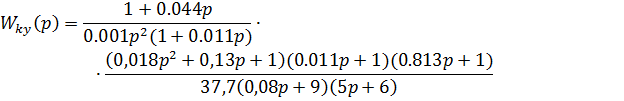
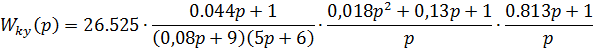
Регулятор включает в себя следующие звенья:

1. П-регулятор Кп=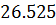

2. ПД-регулятор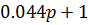

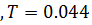
3. Два первогоАпериодическое 2-го порядка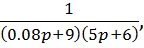

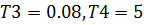
4. ПИД-регулятор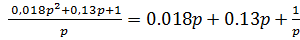

5. ПИ-регулятор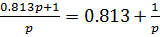

Запишем передаточную функцию скорректированной САУ:

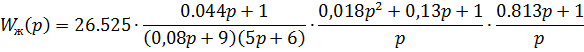
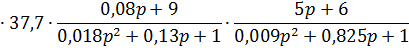
Смоделируем скорректированную САУ в Matlab (рис. 14).

Рис. 14. Блок-схема скорректированной САУ.

Построим ЛАЧХ и ЛФЧХ (рис. 15).

Изм.

Лист

№ докум.

Лист

БГТУ. 210100. 12. 000. ПЗ

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

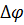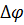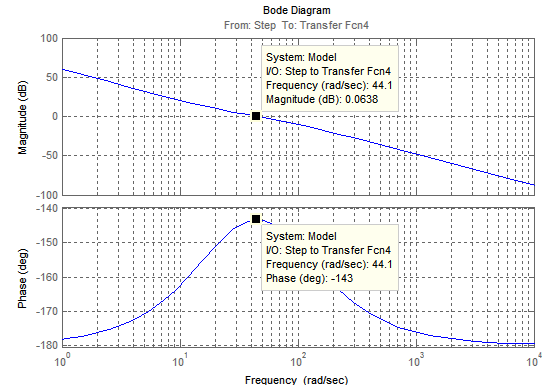
Рис. 15. ЛАЧХ и ЛФЧХ.

Рассчитаем частоту единичного усиления:

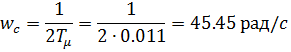
Частоту сопряжения:

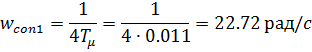
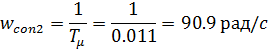
Запас по фазе: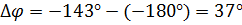

Запас по амплитуде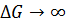

Данное устройство можно упростить, для этого целесообразно провести преобразования в передаточной функции исходной системы.

Передаточная функция исходной системы

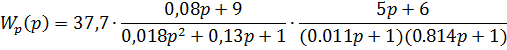
Проанализируем звенья, из которых состоит передаточная функция исходной разомкнутой системы:

Пропорциональное звено Кп=

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

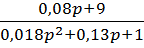Рассмотрим звено , оно состоит из двух звеньев:

1. 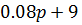-форсирующее звено, его постоянная времени

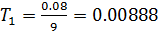
2. 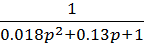-апериодическое звено 2-го порядка,

Постоянная времени 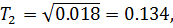постоянная времени 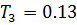, из этого делаем вывод, что 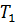можно пренебречь и представить это звено в следующем виде: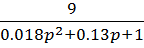

Рассмотрим звено 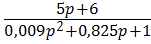, оно состоит из двух звеньев:

1. 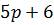- форсирующее звено, его постоянная времени

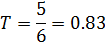
2. 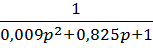- апериодическое звено 2-го порядка,

Постоянная времени 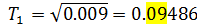, постоянная времени 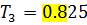, делаем вывод, что постоянные времени соизмеримы друг с другом и поэтому это звено нельзя упростить. Почти 10 раз, проверить возможность. если раскладывается работайте с расложенным

После произведенных упрощений передаточная функция системы примет следующий вид:

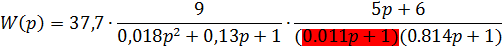
Наименьшая постоянная времени данной системы 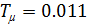другая и т.д. а всё лень матушка. Переделать!

Желаемая передаточная функция системы имеет вид:

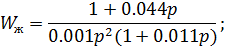
Рассчитаем передаточную функцию корректирующего устройства

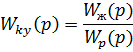
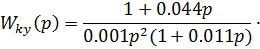
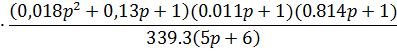
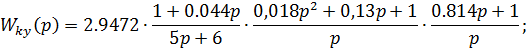
Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

Упрощенное корректирующее устройство состоит из следующих звеньев:

1. П-регулятор Кп=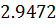

2. ПД-регулятор

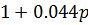
3. Апериодическое 1-го порядка

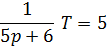
4. ПИД-регулятор

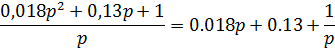
5. ПИ-регулятор

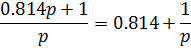
ВЫ ИЗМЕНЯЕТЕ ТОЛЬКО РЕГУЛЯТОР САМА СИСТЕМА ДОЛЖНА БЫТЬ ИСХОДНОЙ!!!!

Запишем передаточную функцию скорректированной САУ:

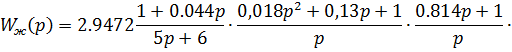
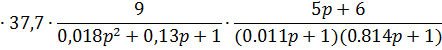
Смоделируем упрощенную скорректированную САУ в Matlab (рис. 16).

Рис. 16. Блок-схема упрощенной скорректированной САУ.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210100. 12. 000. ПЗ

Построим ЛАЧХ и ЛФЧХ упрощенной скорректированной САУ (рис.17).

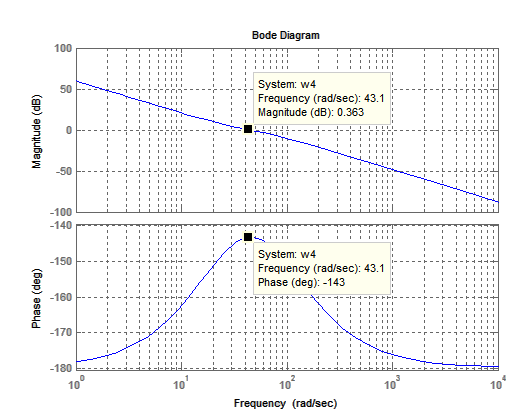
Рис. 17. ЛАЧХ и ЛФЧХ упрощенной САУ.

Рассчитаем частоту единичного усиления

Частоту сопряжения

Определим запас по фазе:

Запас по амплитуде