За даним графіком визначте проміжки спадання функції. 3.Розв’яжіть нерівність х(х – 3) > 0

А) (0; 1); Б) [1; +∞);

В) (–∞; 1); Г) (0; +∞).

3.Розв’яжіть нерівність х(х – 3) > 0 .

А) (–∞; 0)U(3; +∞); Б) [0; 3];

В) (–∞; 0]U[3; +∞); Г) (0; 3).

4. Дано арифметичну прогресію з різницею, що дорівнює 5 та п’ятим членом 12. Знайдіть шостий її член.

А) 17; Б) 37; В) 41; Г) 85.

5. Для поповнення шкільної бібліотеки було витрачено 2400 грн., з яких 18% – на книги з математики. Скільки грошей було витрачено на придбання книг з математики?

А) 400 грн.; Б) 420 грн.; В) 432 грн.; Г)408грн.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6. Спростіть вираз .

7. Знайдіть область визначення функції y= .

ІІІ частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8. Із пунктів А і В, розташованих на відстані 100 км, назустріч один одному одночасно виїхали два велосипедисти. Через 4 год вони зустрілися. Після зустрічі швидкість першого велосипедиста, що рухався з А до В зросла на 5 км/год, а швидкість другого – на 10 км/год. Знайдіть початкову швидкість другого велосипедиста, якщо перший прибув до пункту В на 1 год раніше, ніж другий до пункту А.

Варіант 15

І частина (5 балів)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1. Знайдіть множину розв’язків системи нерівностей

А) х > 5; Б) x > 4; В) x < 5; Г) розв’язків немає.

2.За даним графіком визначте проміжки, на яких функція приймає додатні значення:

А) ; Б) ;

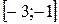В) ; Г) .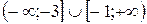

3. Розв’яжіть нерівність (х – 2)(х – 4) < 0.

А) (–∞; 2)U(4; +∞); Б) [2; 4];

В) (–∞; 2]U[4; +∞); Г) (2; 4).

4. Арифметичну прогресію (а_n) задано формулою загального члена . Знайдіть а₄₇.

А) 138; Б) 140; В) 142; Г) 47.

5. Який відсотковий вміст заліза в залізній руді, якщо в 400 г залізної руди міститься 284 г заліза.

А) 71%; Б) 7,1%; В) 0,71 %; Г) 0,071%.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6. Спростіть вираз

7. Відомо, що . Порівняйте: а) і б) і

ІІІ частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8.Сума членів нескінченно спадної геометричної прогресії дорівнює суми квадратів її членів. Знайдіть суму семи перших її членів, якщо другий член дорівнює - 6.

Варіант 16

І частина (5 балів)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1.Знайдіть множину розв’язків системи нерівностей

А) [4; +∞); Б) (4; + ∞); В) (3; 4); Г) [3; 4).

2. За даним графіком визначте проміжки, на яких функція приймає від’ємні значення:

А) (–∞; –2]; Б) (–3; –1);

В) [–3; –1]; Г) (–∞; –3) 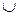(–1; +∞).

3. Розв’яжіть нерівність (х – 3)(х – 1) ≤ 0.

А) (–∞; 1)U(3; +∞); Б) [1; 3];

В) (–∞; 1]U[3; +∞); Г) (1; 3).

4.Арифметичну прогресію (а_n) задано формулою загального члена . Знайдіть а₃₈.

А) 38; Б) 75; В) 77; Г) – 75.

5. Знайдіть відсотковий вміст хрому в чавуні, якщо 300 кг чавуна містять 21 кг хрому.

А) 70%; Б) 14%; В) 7%; Г)1,4%.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6. Спростіть вираз

7. Відомо, що . Порівняйте: а) і б) і

ІІІ частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8. Сума членів нескінченно спадної геометричної прогресії дорівнює 3, а сума кубів усіх її членів дорівнює . Знайдіть прогресію і суму п'яти перших її членів.

Варіант 17

І частина (5 балів)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1. Вираз має зміст, якщо:

А) х 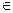(–∞; 10]; Б) х 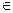[10; +∞); В) х 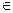(10; +∞); Г) х 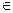(–∞; 10).