Вязкость газов (внутреннее трение)

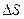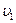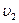Пусть газ течет слоями перпендикулярно оси Х, причем скорость течения слоев убывает по оси Х (рис.12). Перпендикулярно оси Х расположим площадку , по этой площадке соприкасаются два соседних слоя со скоростями течения и .В слоях на хаотичное движение молекул накладывается направленное движение,

причем импульсы направленного движения молекул в соприкасающихся слоях различные ( 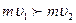). В виду хаотичного движения, молекулы верхнего слоя будут переносить свое количество движения в нижний слой, увеличивая его скорость, а наоборот, молекулы нижнего слоя будут переходить в верхний слой, уменьшая его скорость. В результате возникает сила трения, которая будет действовать вдоль площади 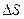параллельно скорости потока слоев. В данном случае переносимой молекулами физической характеристикой является количество движения, т.е. .

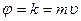Предположим, что во всем объеме концентрация молекул постоянная величина. Тогда

,

,

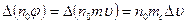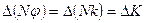где 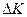- изменение количества движения одного слоя относительно другого за время 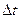по пограничной площадке 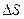. Согласно II закону Ньютона

,

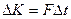где 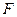-сила взаимодействия между слоями газа, действующие в плоскости соприкосновения слоев, называемая силой внутреннего трения. Таким образом,

.

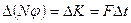Подставляя приведенные выражения для 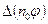и 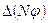в уравнение переноса, получим:

,

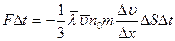или

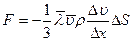. (4.16)

В термодинамике необратимых процессов это явление описывается уравнением Ньютона, записанным в виде:

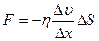, (4.17)

где 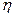- коэффициент внутреннего трения или вязкость. Как следует из (4.16) и (4.17)

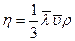. (4.18)

Коэффициент 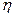, входящий в (4.17) называют динамической вязкостью. Единица измерения 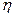в системе СИ 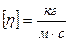. Коэффициент, определяемый выражением 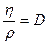, называют кинематической вязкостью, .

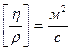Рассмотрим зависимость вязкости от термодинамических параметров давления и температуры. Как было показано в случае коэффициента теплопроводности, произведение 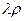не зависит от давления, тогда вязкость также не будет зависеть от давления. Вязкость, также как и коэффициент теплопроводности, должен зависеть от температуры, так как в выражении (4.18) входит средняя скорость тепловых движений молекул, зависящая от температуры по закону 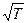. Значит, коэффициент вязкости также должен расти с повышением температуры пропорционально 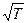. В действительности, вязкость растет несколько быстрее, чем 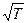. Это связано с тем, что с повышением температуры не только растет тепловая скорость молекул, но и уменьшается эффективное поперечное сечение молекул, и поэтому растет длина свободного пробега.