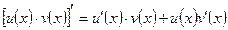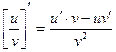Дәріс. Сызықтық алгебра.
ПӘНДЕРДІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕНІ
«Математика 1»
5B073100– „Тіршілік әрекетінің қауіпсіздігі және қоршаған ортаны қорғау“ мамандықтар
үшін
ОҚУ -ӘДІСТЕМЕЛІК МАТЕРИАЛДАР
Семей
Мазмұны
1 Глоссарийлар…………..…………………………………………………….3
2 Дәріс оқулар …………………………………………………………………9
3 Практикалық сабақтар........………………………………………………..31
4 Студенттің өздік жумысы...................………………………………….....51
ГЛОССАРИЙ
| № | Жаңа ұғымдар | Мазмұны | |
| Екінші ретті анықтауыш | 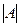 = det A = = det A = 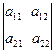 =а11а22 – а21а12 =а11а22 – а21а12 | ||
| Үшінші ретті анықтауыш | 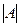 = det A = = det A = 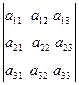 = а11 а22 а33 +а12 а11 а23 а31 +а13 а21 а32 -а13 а22 а31 -а12 а21 а33 -а11 а23 а32 = а11 а22 а33 +а12 а11 а23 а31 +а13 а21 а32 -а13 а22 а31 -а12 а21 а33 -а11 а23 а32 | ||
| Минор | М23= 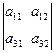 | ||
| Алгебралық толықтауыш | Аij=(-1)i+j 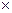 Mij Mij | ||
| Матрица | . А= 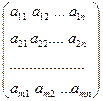 | ||
| Кері матрица | А-1  = = 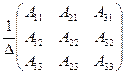 , , 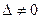 | ||
| Вектор | 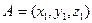 , , 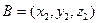 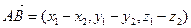 - вектордың координаталар. - вектордың координаталар. 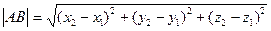 -АВ кесіндінің ұзындығы -АВ кесіндінің ұзындығы  , , 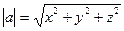 - вектордың ұзындығы - вектордың ұзындығы | ||
| Скалярлық көбейтіндісі | ( 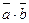 )= )= 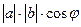 ( ( 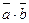 )= )= 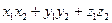 cos cos 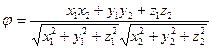 -Угол между векторами. -Угол между векторами. 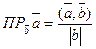 - проекция вектора - проекция вектора 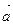 на вектор на вектор 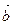 . .  - условие коллинеарности векторов - условие коллинеарности векторов | ||
| Векторлық көбейтіндісі | 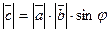 = Sпар. с= = Sпар. с=  = ( = ( 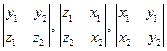 ) S= ) S= 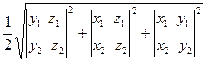 -ұшбұрыштын ауданы (векторлық көбейтіндісінің геометриялық мағынасы) -ұшбұрыштын ауданы (векторлық көбейтіндісінің геометриялық мағынасы) | ||
| Смешанное произведение | (  )= )=  Егер ( Егер (  )=0, онда векторлар компланар болады. V= )=0, онда векторлар компланар болады. V=  - параллелепипедтің көлемі (аралас көбейтіндісінің гелметриялық мағынасы) - параллелепипедтің көлемі (аралас көбейтіндісінің гелметриялық мағынасы) | ||
| Жазақтықтағы түзудін теңдеуі | Ах+Ву+С=0 – жалпы теңдеу к=  - бұрыштық коэффициент - бұрыштық коэффициент  -екі нүктеден өтетін түзудің теңдеуі A(x-x0)+B(y-y0)=0 – нормалі бар түзудің теңдеуі -екі нүктеден өтетін түзудің теңдеуі A(x-x0)+B(y-y0)=0 – нормалі бар түзудің теңдеуі  - бағыттылған вектормен берілген түзудің теңдеуі y-y0=k(x-x0) – бұрыштық коэффициентпен берілген түзудің теңдеуі - бағыттылған вектормен берілген түзудің теңдеуі y-y0=k(x-x0) – бұрыштық коэффициентпен берілген түзудің теңдеуі  - кесінді арқылы түзудің теңдеуі к1 = к2 – түзулердің параллель шарты к1 = - кесінді арқылы түзудің теңдеуі к1 = к2 – түзулердің параллель шарты к1 =  - түзулердің перпендикуляр шарты tg - түзулердің перпендикуляр шарты tg  - түзулердің арасындағы бұрыш d= - түзулердің арасындағы бұрыш d=  - нүктеден түзуге дейінгі қашықтық - нүктеден түзуге дейінгі қашықтық | ||
| Екінші ретті қисықтар | 1)  - эллипс, - эллипс, 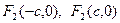 - фокустар, мұндағы - фокустар, мұндағы 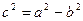 , , 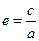 -эксцентриситет, -эксцентриситет, 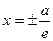 - директрисссалар 2) - директрисссалар 2)  -гипербола, -гипербола, 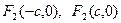 - фокустар, где - фокустар, где 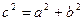 , , 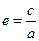 -эксцентриситет, -эксцентриситет, 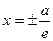 - директриссалар, - директриссалар, 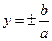 - асимптоталар 3) у2=2px және х2 =2ру –парабола, р – параболаның параметрі, - асимптоталар 3) у2=2px және х2 =2ру –парабола, р – параболаның параметрі, 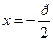 - директрисса, - директрисса, 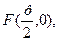 - параболаның фокусы - параболаның фокусы 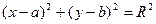 -шеңбер, С(а,в) – шеңбердің центрі, R – шеңбердін радиусы. -шеңбер, С(а,в) – шеңбердің центрі, R – шеңбердін радиусы. | ||
| Кеңістіктегі тұзудің теңдеудің | 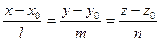 - тұзудің канондық теңдеуі, - тұзудің канондық теңдеуі, 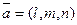 - бағыттылған вектор - бағыттылған вектор 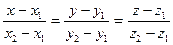 - екі нүктеден өтетін тузудің теңдеуі - екі нүктеден өтетін тузудің теңдеуі 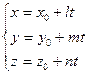 - түзудің параметрлік теңдеуі - түзудің параметрлік теңдеуі 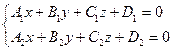 - уравнение прямой как пересечение двух плоскостей, где - уравнение прямой как пересечение двух плоскостей, где 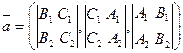 - бағыттылған вектор - бағыттылған вектор 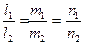 - түзулердің параллель шарты l1l2+m1m2+n1n2=0– түзулердің перпендикуляр шарты - түзулердің параллель шарты l1l2+m1m2+n1n2=0– түзулердің перпендикуляр шарты | ||
| Жазықтықтың теңдеуі | Ax+By+Cz+D=0 - Жалпы теңдеуі A(x-x0)+B(y-y0)+C(z-z0)=0, где 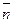 =(A,B,C) – жазықтықтың нормалі =(A,B,C) – жазықтықтың нормалі 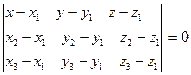 - Үш нуктедең өтетін жазақтықтын теңдеуі d= - Үш нуктедең өтетін жазақтықтын теңдеуі d= 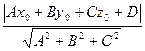 - нүктеден жазықтыққа дейінгі қашықтық - нүктеден жазықтыққа дейінгі қашықтық | ||
| Шектер | Ақырсыз үлкен және ақырсыз кіші функциялардың қасиеттері 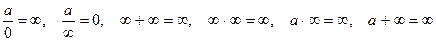 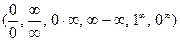 - анықталмандықтар - анықталмандықтар 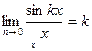 , , 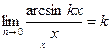 , , 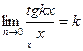 , , 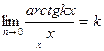 бірінші тамаша шек бірінші тамаша шек 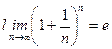 , , 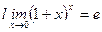 , , 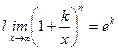 , , 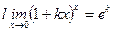 , , 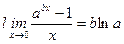 , , 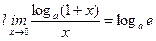 Екінші тамаша шек Екінші тамаша шек | ||
| Функцияның туындысы | 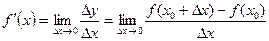 -анықтама -анықтама 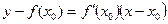 - жанаманың теңдеуі (геометриялық мағынасы) Ережелер: - жанаманың теңдеуі (геометриялық мағынасы) Ережелер: 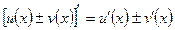 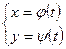 , , 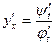 - параметрлік функцияның туындысы 1. - параметрлік функцияның туындысы 1. 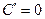 2. 2. 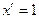 6. 6. 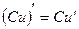 7. 7. 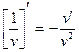 8. 8. 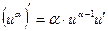 9. 9. 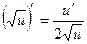 10. 10. 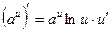 11. 11. 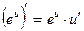 12. 12. 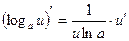 13. 13. 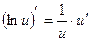 14. 14. 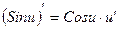 15. 15. 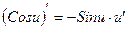 16. 16. 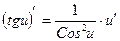 17. 17. 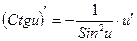 18. 18. 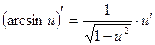 19. 19. 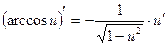 20. 20. 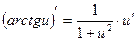 21. 21. 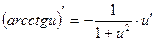 | ||
| Лопиталь ережесі | 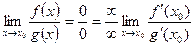 | ||
| Функияны зерттеу | Анықталу облысы: а) егер 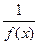 , онда , онда 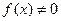 б) егер б) егер 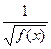 , онда , онда 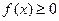 в) егер в) егер 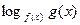 , онда , онда 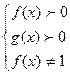 г) егер г) егер 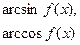 , онда , онда 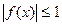 Жұп және тақ функцияға зерттеу: Егер Жұп және тақ функцияға зерттеу: Егер 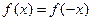 , онда , онда 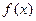 - жұп болады, графигі ОУ өсіне қатысты симметриялы болады. Егер - жұп болады, графигі ОУ өсіне қатысты симметриялы болады. Егер 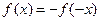 , онда , онда 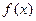 - тақ болады, графигі бас координат нүктесіне қатысты симметриялы болады. - тақ болады, графигі бас координат нүктесіне қатысты симметриялы болады. | ||
| Графигінің өспелі және кемімелі аралықтарға зерттеу | Егер 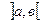 интервалында интервалында 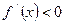 , онда бұл интервалда графигі кемийд, ал егер- , онда бұл интервалда графигі кемийд, ал егер- 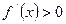 , онда графигі өспелі болады. Егер , онда графигі өспелі болады. Егер 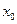 нүктесінің нүктесінің 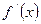 туындысы сол жағында туындысы сол жағында 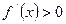 , ал оң жағында , ал оң жағында 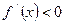 болса онда болса онда 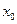 нүктесі максимум болады. Егер керісінші , онда нүктесі максимум болады. Егер керісінші , онда 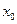 минимум болады. минимум болады. | ||
| Графигінің дөңістігі және ойыстігі, иілу нұтелері | 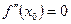 Иілу ніктенің қажетті белгісі (жеткілікті шарты) Егер Иілу ніктенің қажетті белгісі (жеткілікті шарты) Егер 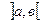 интервалында интервалында 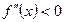 , онда бұл интервалда графигі дөнес болады, ал егер- , онда бұл интервалда графигі дөнес болады, ал егер- 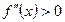 , онда графигі ойыс болады. Егер , онда графигі ойыс болады. Егер 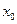 нүктесінің оң жағы мен сол жағында екінші ретті туындысы нүктесінің оң жағы мен сол жағында екінші ретті туындысы 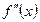 танбасын өзгертетін болса, онда ол нүктесінде иілу нүктесі болады. танбасын өзгертетін болса, онда ол нүктесінде иілу нүктесі болады. | ||
| Асимптоталар | Егер 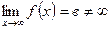 , онда у=в – горизонтал асимптотасы болады. Егер , онда у=в – горизонтал асимптотасы болады. Егер 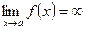 , онда , онда 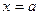 - вертикал асимптота. Егер - вертикал асимптота. Егер 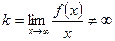 , , 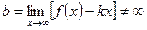 , онда y=kx+b - көлбеу асимптота. , онда y=kx+b - көлбеу асимптота. | ||
| Анықталмаған интеграл | 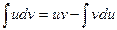 - бөлшектеп интегралдау. Негізгі интегралдың таблицасы. 1. - бөлшектеп интегралдау. Негізгі интегралдың таблицасы. 1. 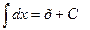 2. 2. 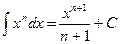 3. 3. 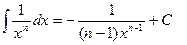 4. 4. 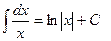 5. 5. 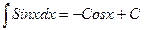 6. 6. 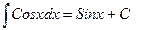 7. 7. 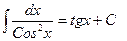 8. 8. 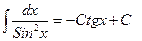 9. 9. 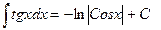 10. 10. 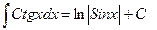 11. 11. 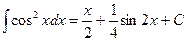 12. 12. 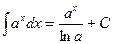 13. 13. 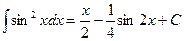 14. 14. 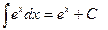 15. 15. 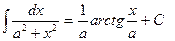 16. 16. 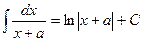 17. 17. 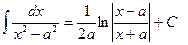 18. 18. 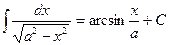 19. 19. 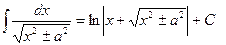 20. 20. 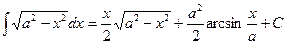 21. 21. 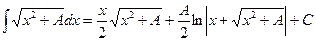 22. 22. 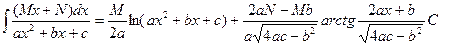 23. 23. 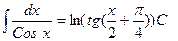 24. 24. 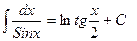 | ||
| Қарапайым рационал бөлшектер | 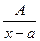 ; ; 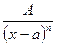 ; ; 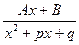 ; ; 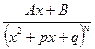 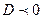 | ||
| Тригонометриялық функцияларды интгралдау | 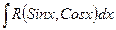 . .  Универсалдық ауыстыру Универсалдық ауыстыру 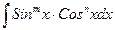 а) егер n және m – жүп болса. а) егер n және m – жүп болса. 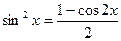 и и 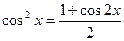 б) егер n немесе m – тақ болса. б) егер n немесе m – тақ болса. 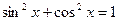 , , 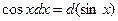 или или 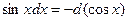 в) егер n + m – жұп, теріс болса. в) егер n + m – жұп, теріс болса. 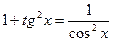 и и 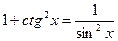 , , 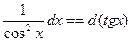 , , 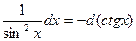 | ||
| Иррационал функцияларды интегралдау | 1. 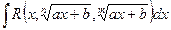 ,ауыстыру ,ауыстыру 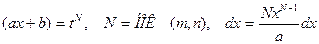 2. а) 2. а) 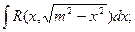 ауыстыру ауыстыру 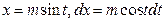 б) б) 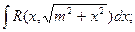 ауыстыру ауыстыру 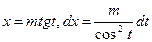 в) в) 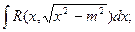 ауыстыру ауыстыру 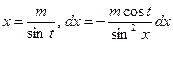 3. 3. 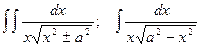 замена замена 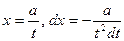 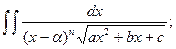 ауыстыру ауыстыру 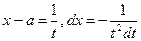 4. 4. 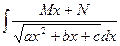 , ауыстыру , ауыстыру 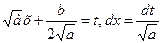 | ||
| Анықталған интегралдың геометриялық қолданулары | 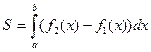 , , 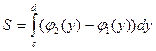 - ауданы - ауданы 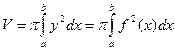 - көлемі - көлемі 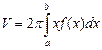 көлемі көлемі 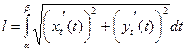 , , 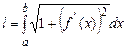 - доғаның ұзындығы - доғаның ұзындығы | ||
ДӘРІС ОҚУЛАР
Дәріс сабақтардың құрылымы
Дәріс. Сызықтық алгебра.
Анықтама. mжатық және n тік жолдарда орналасқан сандар кестесін m 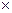 n өлшемді тік бұрышты А матрицасы деп атайды. Яғни
n өлшемді тік бұрышты А матрицасы деп атайды. Яғни
А= 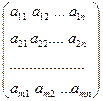
Айталық
А= 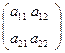
екінші ретті квадрат матрица берілсін.
Анықтама. Екінші ретті квадрат А матрицасына сәйкесті екінші ретті анықтауыш деп санды атайды және былай белгілейді
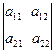 =а11а22 – а21а12
=а11а22 – а21а12
Мысал. Мына анықтауышты 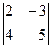 есептеу керек
есептеу керек
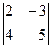 =
=