Вариационная постановка

Постановка задачи

МКЭ для двумерной краевой задачи для эллиптического уравнения в полярной 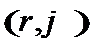системе координат. Базисные функции билинейные на прямоугольниках. Краевые условия всех типов. Коэффициент диффузии 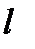разложить по биквадратичным базисным функциям. Матрицу СЛАУ генерировать в разреженном строчном формате. Для решения СЛАУ использовать МСГ или ЛОС с неполной факторизацией.

Решаемое уравнение

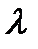-div( grad )+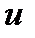

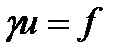
задано в некоторой области с границей .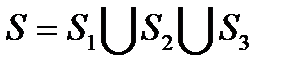

В полярной системе координат:

.

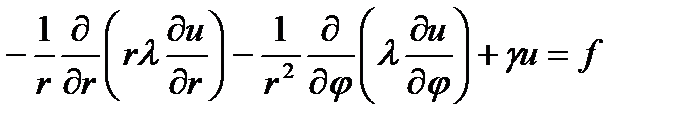Краевые условия

, ,

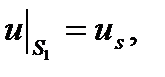
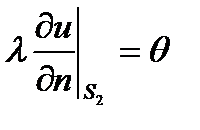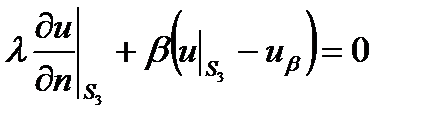Расчетная область

Расчётная область разбивается на прямоугольники, содержащие по четыре узла.

Локальная нумерация выглядит следующим образом:

Теоретическая часть

Вариационная постановка

Запишем для исходной краевой задачи эквивалентную вариационную постановку в форме уравнения Галёркина, для этого правую и левую часть исходного уравнения домножим на функцию 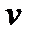из пространства пробных функций 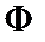и проинтегрируем по :

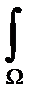(-div( 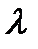grad )+ .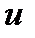

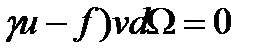
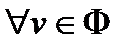Преобразуем полученное уравнение с использованием формулы Грина:

- .

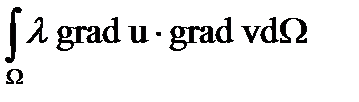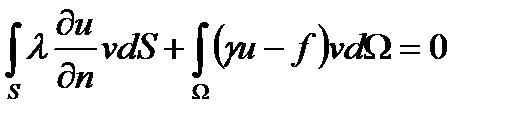
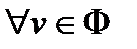Воспользовавшись краевыми условиями преобразуем интегралы:

- .

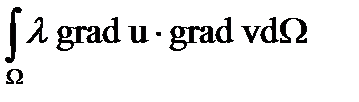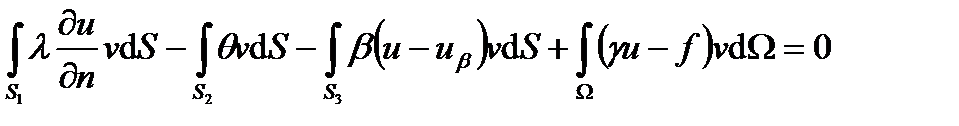
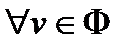В качестве 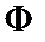выберем 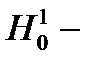пространство пробных функций 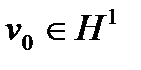, которые на границе S­₁ удовлетворяют нулевым первым краевым условиям. При этом будем считать, что 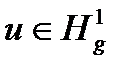, где 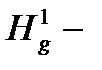множество функций, имеющих суммируемые с квадратом первые производные и удовлетворяющих только первым краевым условиям на границе S₁:

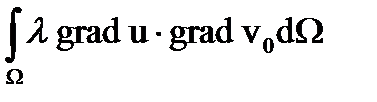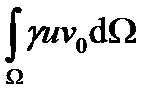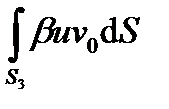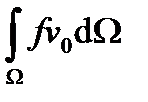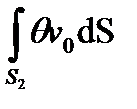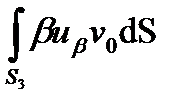+ + = + + . (1.1)