Проекции конуса. Изображение конуса на чертеже. Точка и линия на поверхности конуса.

Цилиндр и конус. Проекции цилиндра и конуса показаны на рис. 127, а и б. Круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций; проекции оснований на горизонтальную плоскость будут также кругами.

Фронтальная и профильная проекция цилиндра - прямоугольники, а конуса - равнобедренные треугольники.

На рис. 127в, дан чертеж усеченного конуса, горизонтальная проекция которого представляет собой две окружности, а фронтальная проекция - равнобочную трапецию.

Выполнение чертежей цилиндра и конуса начинают с проведения осей симметрии.

Из рис. 127, а видно, что фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. На рисунке они даны лишь для того, чтобы показать, какую форму имеют все три проекции цилиндра и конуса.

Размеры цилиндра и конуса определяются высотой h и диаметром основания d. Для усеченного конуса указывают высоту h и диаметры обоих оснований D и d.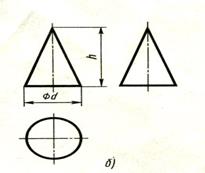

Точки на поверхности вращения. Положение точки на по­верхности вращения определяют по принадлежности точки ли­нии каркаса поверхности, т. е. с помощью окружности, проходящей через эту точку на поверхности вращения. В слу­чае линейчатых поверхностей для этой цели возможно приме­нение и прямолинейных образующих.

Применение параллели и прямолинейной образующей для построения проекций точек, принадлежащих данной поверхности вращения, показано на рисунке 7.12. Если дана проекция m' то проводят фронтальную проекцию f'f'₁ параллели, а затем радиусом R проводят окружность – го­ризонтальную проекцию параллели – и на ней находят проекцию m. Если бы была задана горизонтальная проек­ция m, то следовало бы провести радиусом

R = om окруж­ность, по точке f построить f' и провести f''f'₁ – фронтальную проекцию параллели – и на ней в проекционной связи отметить точку m'. Если дана проекция n' на линейчатом (коническом) участке поверхности вращения, то проводят фронтальную проекцию d's' очерковой образу­ющей и через проекцию n' – фронтальную проекцию s'k' образующей на поверхности конуса. Затем на горизонталь­ной проекции sk этой образующей строят проекцию п. Если бы была задана горизонтальная проекция n, то сле­довало бы провести через нее горизонтальную проекцию sk образующей, по проекции k' и s' (построение ее было рассмотрено выше) построить фронтальную проекцию s'k' и на ней в проекционной связи отметить проекцию n'.

На рисунке 7.15 показано построение проекций точки К, принадлежащей поверхности

тора. Следует отметить, что по­строение выполнено для видимых горизонтальной проекции к и фронтальной проекции k'.

На рисунке 7.16 показано построение по заданной фрон­тальной проекции m' точки на поверхности сферы ее гори­зонтальной m и профильной m''проекций. Проекция m построена с помощью окружности – параллели, проходящей через проекцию m'. Ее радиус – o–1. Проекция m" построена с помощью окружности, плоскость которой параллельна профильной плоскости проекций, проходящей через проек­цию m'.Ее радиус o"2".

Построение проекций линий на поверхности вращения мо­жет быть выполнено также при помощи окружностей – па­раллелей, проходящих через точки, принадлежащие этой линии.

На рисунке 7.17 показано построение горизонтальной про­екции ab линии, заданной фронтальной проекцией a'b' на по­верхности вращения, состоящей из частей поверхностей сферы, тора, конической. Для более точного вычерчивания горизон­тальной проекции линии продолжим ее фронтальную проек­цию вверх и вниз и отметим проекции 6' и 5' крайних точек. Горизонтальные проекции 6, 1, 3, 4, 5 построены с помощью линий связи. Проекции b, 2, 7, 8, а построены с помощью параллелей, фронтальные проекции которых проходят через проекции b', 2' 7', 8' a' этих точек. Количество и располо­жение промежуточных точек выбирают исходя из формы ли­нии и требуемой точности построения. Горизонтальная проекция линии состоит из участков: b –1 – части эллипса, 3 – 8 – a – 4 – части эллипса,

1 – 2 – 7 – 3 – кривой четвертого порядка (проекция кривой на поверхности тора).

Рис. 7.17