Матричные уравнения контурных токов
Уравнения контурных токов можно записать в матричной форме:
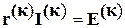 ,
,
где 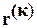 - квадратная матрица контурных сопротивлений;
- квадратная матрица контурных сопротивлений;
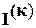 - матрица-столбец контурных токов;
- матрица-столбец контурных токов;
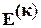 - матрица-столбец контурных ЭДС, учитывающая источники напряжений и эквивалентные ЭДС от источников тока.
- матрица-столбец контурных ЭДС, учитывающая источники напряжений и эквивалентные ЭДС от источников тока.
Матрица контурных сопротивлений 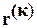 может быть получена по схеме при помощи матрицы контуров
может быть получена по схеме при помощи матрицы контуров 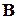 :
:
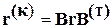 ,
,
где 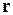 - диагональная матрица сопротивлений ветвей;
- диагональная матрица сопротивлений ветвей;
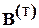 - транспортированная матрица контуров.
- транспортированная матрица контуров.
Рассмотрим схему, приведенную на рисунке 2.24. Направление обхода каждого контура совпадает с положительным направлением соответствующего контурного тока, а направление ветвей – с положительными направлениями токов в ветвях.
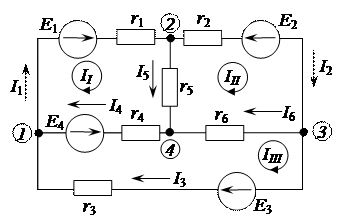
Рисунок 2.24 – Электрическая цепь постоянного тока
Граф электрической цепи, с выбранным деревом из четвертой, пятой и шестой ветви, приведен на рисунке 2.25.
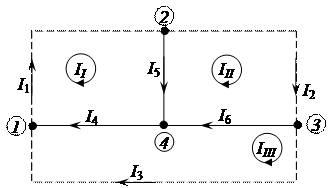
Рисунок 2.25 – Граф цепи постоянного тока
В данной схеме, независимые контуры содержат контурные токи 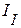 ,
, 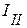 ,
, 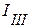 , что соответствует первой, второй и третьей ветвям связи.
, что соответствует первой, второй и третьей ветвям связи.
Матрица контуров 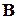 состоит из трех строк и шести столбцов:
состоит из трех строк и шести столбцов:
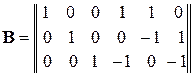 .
.
Диагональная матрица сопротивлений 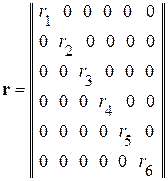 .
.
Произведение матриц 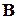 и
и 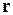 равно:
равно:
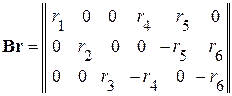 .
.
Квадратная матрица контурных сопротивлений 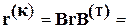
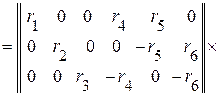
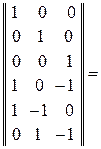
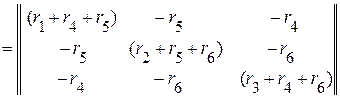 .
.
Матрица-столбец контурных токов 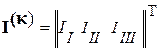 .
.
Матрица-столбец контурных ЭДС
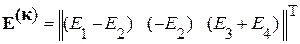 .
.
Пользуясь матрицами 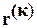 ,
, 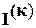 ,
, 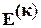 и уравнением
и уравнением 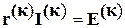 , можно получить систему уравнений, составленную на основании второго закона Кирхгофа для контуров, каждый из которых включает только одну ветвь связи.
, можно получить систему уравнений, составленную на основании второго закона Кирхгофа для контуров, каждый из которых включает только одну ветвь связи.
Матрица токов ветвей 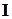 определяется через матрицу контурных токов
определяется через матрицу контурных токов 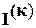 по формуле
по формуле 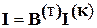 .
.
Например, для электрической цепи (рис. 2.24):
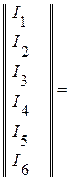
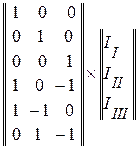 .
.
Из этого матричного уравнения получаем равенства, определяющие токи ветвей через контурные токи:
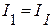 ;
; 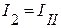 ;
; 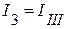 ;
; 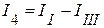 ;
; 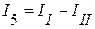 ;
; 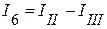 .
.
Пример 2.9.Решить задачу, приведенную в примере 2.5 с помощью матричных уравнений контурных токов.
Матрица контуров В состоит из пяти строк и десяти столбцов:
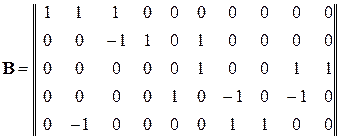 .
.
Диагональная матрица сопротивлений
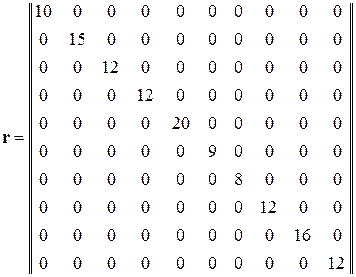 .
.
Произведение матриц 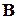 и
и 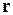 равно:
равно:
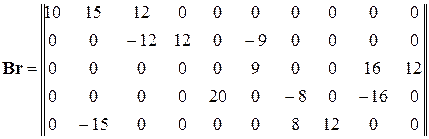 .
.
Квадратная матрица контурных сопротивлений 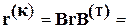
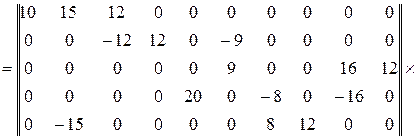

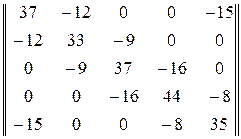 .
.
Матрица-столбец контурных токов
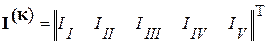 .
.
Матрица-столбец контурных ЭДС
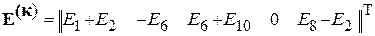 .
.
Определяем матрицу контурных токов 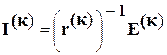 =
=
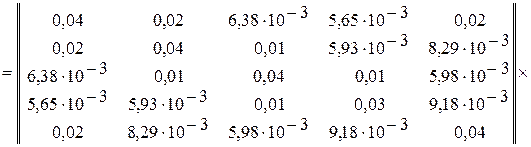
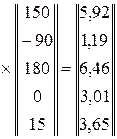 .
.
Контурные токи соответственно равны
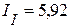 А,
А, 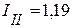 А,
А, 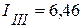 А,
А,
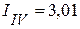 А,
А, 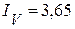 А.
А.
Матрица токов ветвей 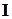 определяем через матрицу контурных токов
определяем через матрицу контурных токов 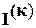 :
:
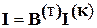
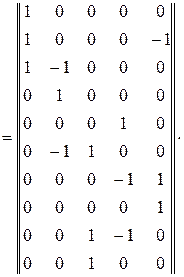
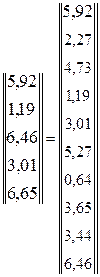 .
.
Токи в ветвях соответственно равны
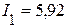 А,
А, 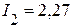 А,
А, 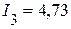 А,
А, 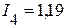 А,
А, 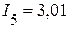 А,
А,
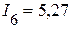 А,
А, 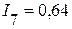 А,
А, 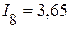 А,
А, 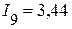 А,
А, 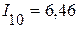 А.
А.
Токи, рассчитанные в примерах 2.5 и 2.9, совпадают.
Метод узловых потенциалов
Метод узловых потенциалов для электрических
Схем общего вида
Идея метода узловых потенциалов (МУП). Один из узлов схемы заземляется и его потенциал принимается равным нулю. Далее определяются потенциалы остальных узлов, что дает возможность определить напряжения на зажимах каждой ветви. Затем, используя закон Ома (рис. 2.26), определяем токи в ветвях.
Запишем выражения закона Ома для различных участков цепи, приведенных на рисунке 2.26.
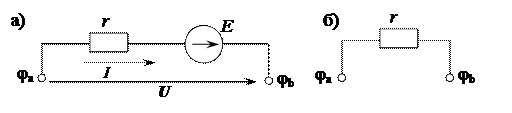
Рисунок 2.26. – Закон Ома: а) с источником напряжения;
б) без источника напряжения
Для участка цепи, содержащего источник напряжения:
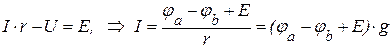 .
.
Для участка цепи, не содержащего источник напряжения:
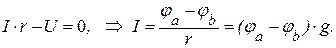
Таким образом, для определения тока к ветвях, необходимо определить потенциалы узлов (напряжения на зажимах ветвей).
Выведем систему уравнений для определения потенциалов узлов произвольной схемы. Для этого используем закон Ома и первый закон Кирхгофа.
Допустим, имеется схема, приведенная на рисунке 2.27.
Заземлим 3 узел, тогда потенциал φ3 = 0.
Потенциалы остальных узлов будут соответственно φ1 и φ2.
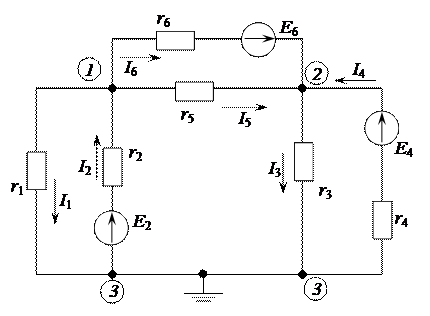
Рисунок 2.27 – Электрическая цепь
Используя закон Ома, запишем уравнения для токов в каждой ветви.
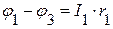 =>
=> 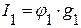 ,
,
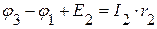 =>
=> 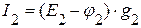 ,
,
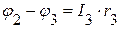 =>
=> 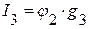 ,
,
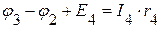 =>
=> 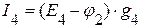 ,
,
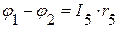 =>
=> 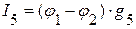 ,
,
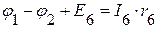 =>
=> 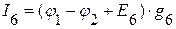 .
.
Уравнения по первому закону Кирхгофа для первого и второго узлов имеют вид:
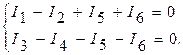
В полученную систему уравнений подставим уравнения для токов, составленных по закону Ома. В результате получим:
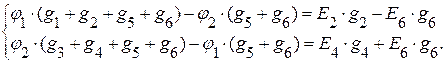
Имеем два уравнения с двумя неизвестными потенциалами φ1 и φ2.
Рассмотрим свойства полученных уравнений.
При составлении первого уравнения потенциал φ1 умножается на сумму проводимостей ветвей, подсоединённых к этому узлу. Влияние потенциала второго узла осуществляется путем введения элемента 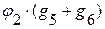 . Этот элемент берется всегда со знаком ”-”. Слагаемое
. Этот элемент берется всегда со знаком ”-”. Слагаемое 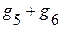 является арифметической суммой проводимостей ветвей, соединяющих 1 и 2 узел.
является арифметической суммой проводимостей ветвей, соединяющих 1 и 2 узел.
В правой части уравнения записывается алгебраическая сумма токов источников питания ветвей, подсоединенных к данному узлу. Если ЭДС источника направлена к узлу, то произведение 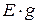 берется со знаком ”+”, если от узла – со знаком ”-“.
берется со знаком ”+”, если от узла – со знаком ”-“.
Используя вышеуказанные свойства запишем систему уравнений для определения потенциалов произвольной схемы.
Допустим, имеется электрическая схема, содержащая n + 1 узлов. Заземляем один узел и имеем n неизвестных потенциалов (соответственно n уравнений).
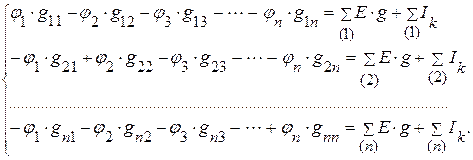
где 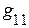 ,
, 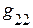 ,
, 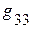 , … ,
, … , 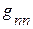 – соответственно сумма проводимостей ветвей, подсоединённых соответственно к 1, 2 … n – ному узлу (всегда со знаком +).
– соответственно сумма проводимостей ветвей, подсоединённых соответственно к 1, 2 … n – ному узлу (всегда со знаком +).
где 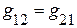 и
и 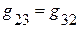 – сумма проводимостей ветвей, соединяющих непосредственно 1 и 2 узел и т.д.
– сумма проводимостей ветвей, соединяющих непосредственно 1 и 2 узел и т.д.
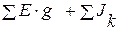 – сумма токов источников питания.
– сумма токов источников питания.
Пример 2.10.Рассмотрим рекомендованный порядок решения МУП на конкретном примере электрической цепи, приведенной на рисунке 2.28, с параметрами E3 = 30 (B), Е2 = 20 В, Е5 = 50 В, r1 = 20 Ом, r2 = 10 Ом, r3= 8 Ом, r4 = 10 Ом, r5 = 10 Ом, r6 = 5 Ом, Jk = 3 А.
1. Осуществляем предварительный анализ схемы. Количество ветвей – 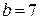 , количество узлов –
, количество узлов – 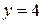 .
.
Потенциал третьего узла принимаем равным нулю: 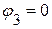 . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы 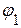 ,
, 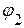 ,
,  .
.
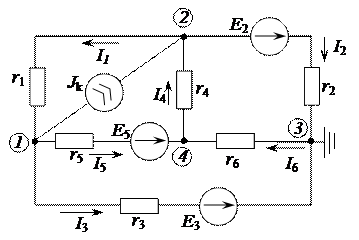
Рисунок 2.28 – Электрическая цепь постоянного тока
2. Составляем уравнения для определения потенциалов  ,
,  ,
,  :
:
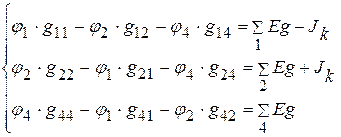
3. Подставляем числовые значения и решаем систему уравнений.
3.1. Проводимости ветвей
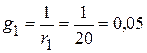 См;
См;
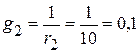 См;
См;
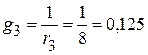 См;
См;
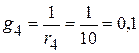 См;
См;
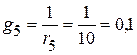 См;
См;
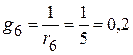 См.
См.
3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
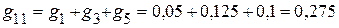 См;
См;
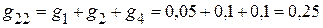 См;
См;
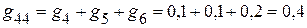 См.
См.
Сумма проводимостей, соединяющих различные узлы
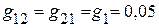 См;
См;
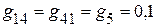 См;
См;
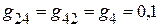 См.
См.
Узловые токи 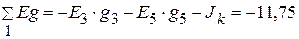 А,
А,
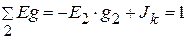 А,
А,
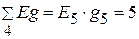 А.
А.
3.2. После подстановки цифровых данных система имеет вид
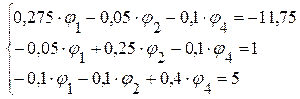
3.3. Решая данную систему уравнений произвольным методом, определяем потенциалы:
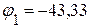 В,
В,
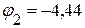 В,
В,
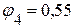 В.
В.
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.28.
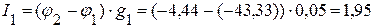 А,
А,
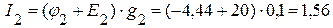 А,
А,
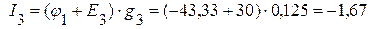 А,
А,
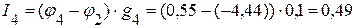 А,
А,
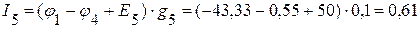 А,
А,
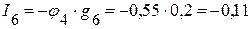 А.
А.
4. Определяем напряжение на зажимах источника тока. Из контура 121:
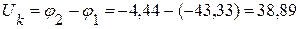 В.
В.
5. Проверяем решение системы уравнений, составив баланс мощностей.
5.1. Мощность источников:
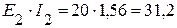 Вт,
Вт,
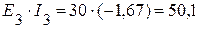 Вт,
Вт,
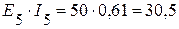 Вт,
Вт,
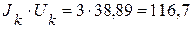 Вт.
Вт.
Знак ”-” указывает на то, что третий источник работает в режиме потребителя электроэнергии (например, зарядка аккумулятора).
Суммарная мощность источников:
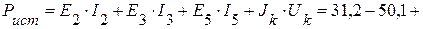
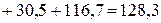 Вт.
Вт.
4.2. Мощность приемников:
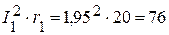 Вт,
Вт,
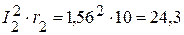 Вт,
Вт,
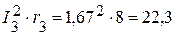 Вт,
Вт,
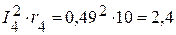 Вт,
Вт,
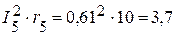 Вт,
Вт,
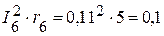 Вт.
Вт.
Суммарная мощность приемников:
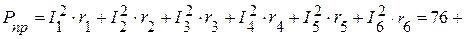
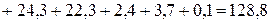 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении 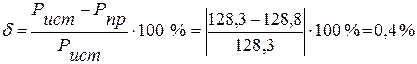 и не превышает 0,5%.
и не превышает 0,5%.
Пример 2.11.Рассмотрим решение задачи, приведенной в примере 2.2, методом узловых потенциалов. Электрическая цепь для рассматриваемого метода, приведена на рисунке 2.29.
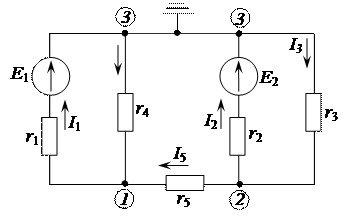
Рисунок 2.29 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. Количество ветвей – 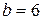 , количество узлов –
, количество узлов – 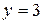 .
.
Потенциал третьего узла принимаем равным нулю: 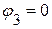 . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы 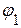 ,
, 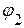 .
.
2. Составляем уравнения для определения потенциалов 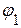 ,
, 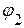 :
:
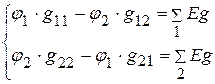
3. Подставляем числовые значения и решаем систему уравнений.
3.1. Проводимости ветвей
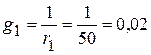 См;
См;
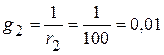 См;
См;
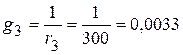 См;
См;
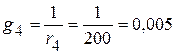 См;
См;
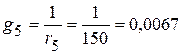 См.
См.
3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
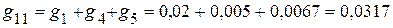 См;
См;
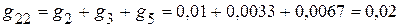 См.
См.
Сумма проводимостей, соединяющих различные узлы
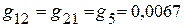 См.
См.
Узловые токи 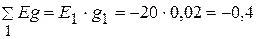 А,
А,
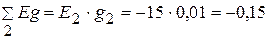 А.
А.
3.2. После подстановки цифровых данных система имеет вид
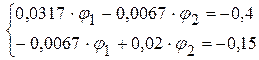
3.3. Решая данную систему уравнений произвольным методом, определяем потенциалы:
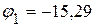 В,
В,
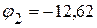 В.
В.
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.29.
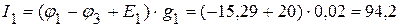 мА,
мА,
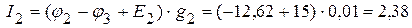 мА,
мА,
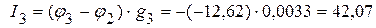 мА,
мА,
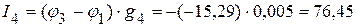 мА,
мА,
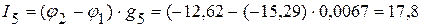 мА.
мА.
Токи в ветвях, рассчитанные в примерах 2.2 и 2.11, совпадают.
