Тестовые задания и задачи для промежуточной аттестации
ДЛЯ ВСЕХ ВИДОВ КОНТРОЛЯ
ПО ДИСЦИПЛИНЕ
«МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
для направления 030300 Психология
Составитель:
К.с.н., доцент Ю.А. Хоменко
Шахты - 2012
Вопросы для промежуточной аттестации к контрольным точкам по дисциплине «Математическая статистика»
Первая контрольная точка
1. Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?
2. Дайте определение суммы событий. Докажите теорему сложения.
3. Дайте определение произведения событий. Докажите теорему умножения.
4. Докажите формулу Бернулли.
5. Докажите формулу полной вероятности.
6. Докажите формулы Бейеса.
7. Дайте определение математического ожидания и докажите его свойства.
8. Дайте определение дисперсии и докажите ее свойства.
9. Дайте определение среднего квадратического отклонения и докажите его преимущества по сравнению с дисперсией.
10. Дайте определение функции распределения и докажите ее свойства.
11. Дайте определение плотности распределения вероятности и докажите ее свойства.
12. Напишите формулы плотности нормального и показательного распределений. Какими параметрами определяются эти распределения?
13. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена: а) нормально, б) показательному закону.
14. Дайте определение функции распределения и плотности распределения вероятностей двумерной непрерывной случайной величины.
15. Как найти вероятность попадания случайной величины в заданную область?
16. Дайте определение случайной функции, сечения и реализации.
17. Дайте определения математического ожидания и дисперсии случайной функции и докажите их свойства.
18. Дайте определение корреляционной функции и перечислите ее свойства.
19. Как, зная корреляционную функцию случайной функции, найти ее дисперсию?
Вторая контрольная точка
20. Сформулируйте и докажите теоремы о характеристиках производной от случайной функции.
21. Сформулируйте и докажите теоремы о характеристиках интеграла от случайной функции.
22. Дайте определение стационарной случайной функции.
23. Сформулируйте и докажите свойства корреляционной функции и от стационарной случайной функции.
24. Напишите формулы для вычисления выборочной средней и выборочной дисперсии.
25. Как построить гистограмму?
26. Дайте определение несмещенной, эффективной и состоятельной оценок.
27. Является ли выборочная дисперсия несмещенной оценкой генеральной дисперсии? Что такое исправленная дисперсия?
28. Для чего служит метод наибольшего правдоподобия? Как им пользоваться для дискретных и непрерывных случайных величин?
29. Как найти доверительные интервалы для оценки математического ожидания нормального распределения?
30. Как найти доверительные интервалы для оценки среднего квадратического отклонения нормально распределенной случайной величины?
31. Какую зависимость называют корреляционной?
32. Какую корреляцию называют линейной?
33. Перечислите свойства выборочного коэффициента корреляции. Как найти этот коэффициент?
34. Напишите выборочное уравнение прямой линии регрессии 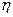 на
на 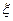 .
.
35. Дайте определение статистической гипотезы.
36. Что называют ошибкой первого (второго) рода?
37. Что такое уровень значимости? Приведите значения уровней значимости, наиболее употребительных на практике.
38. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
39. Моделирование дискретной случайной величины методом Монте-Карло.
40. Моделирование непрерывной случайной величины методом Монте-Карло.
Варианты контрольных работ для промежуточной аттестации
Вариант № 1.
1. Ящик содержит 90 годных и 10 бракованных деталей. Найти вероятность того, что среди 10 вынутых из ящика деталей нет бракованных.
2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?
3. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 5000 выстрелов.
4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий.
5. Случайная величина Х характеризуется рядом распределения
| Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определить математическое ожидание и дисперсию.
Вариант № 2.
1. Ящик содержит 80 годных и 10 бракованных деталей. Найти вероятность того, что среди 5 вынутых из ящика деталей нет бракованных.
2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 6%, 8%. Какова вероятность того, что случайно выбранный болт оказался дефектным?
3. Вероятность попадания в цель при каждом выстреле равна 0,002. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 1000 выстрелов.
4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,2. Построить ряд распределения числа попаданий.
5. Случайная величина Х характеризуется рядом распределения
| Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определить математическое ожидание и дисперсию.
Вариант № 1.
6. Ящик содержит 90 годных и 10 бракованных деталей. Найти вероятность того, что среди 10 вынутых из ящика деталей нет бракованных.
7. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?
8. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 5000 выстрелов.
9. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий.
10. Случайная величина Х характеризуется рядом распределения
| Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определить математическое ожидание и дисперсию.
Вариант № 2.
6. Ящик содержит 80 годных и 10 бракованных деталей. Найти вероятность того, что среди 5 вынутых из ящика деталей нет бракованных.
7. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 6%, 8%. Какова вероятность того, что случайно выбранный болт оказался дефектным?
8. Вероятность попадания в цель при каждом выстреле равна 0,002. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 1000 выстрелов.
9. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,2. Построить ряд распределения числа попаданий.
10. Случайная величина Х характеризуется рядом распределения
| Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определить математическое ожидание и дисперсию.
Вариант № 3.
1. Ящик содержит 70 годных и 7 бракованных деталей. Найти вероятность того, что среди 7 вынутых из ящика деталей нет бракованных.
2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 3%, 5%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?
3. Вероятность попадания в цель при каждом выстреле равна 0,003. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 6000 выстрелов.
4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,4. Построить ряд распределения числа попаданий.
5. Случайная величина Х характеризуется рядом распределения
| Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определить математическое ожидание и дисперсию.
Вариант № 4.
1. Ящик содержит 70 годных и 7 бракованных деталей. Найти вероятность того, что среди 7 вынутых из ящика деталей нет бракованных.
2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 3%, 5%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?
3. Вероятность попадания в цель при каждом выстреле равна 0,003. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 6000 выстрелов.
4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,4. Построить ряд распределения числа попаданий.
5. Случайная величина Х характеризуется рядом распределения
| Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определить математическое ожидание и дисперсию.
Тестовые задания и задачи для промежуточной аттестации
1. Дана выборка -4, -1, 1, 3, 6. Среднее значение равно…
2. Дана выборка -2, 3, 4, 5. Величина дисперсии равна…
3. Для выборки -3, -2, 1, 5, 9. Среднее квадратическое отклонение равно…
4. Случайная величина с плотностью распределения 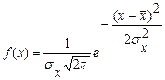 распределена по … закону
распределена по … закону
1. логарифмически нормальному;
2. нормальному;
3. показательному;
4. равномерному.
5. Число коэффициентов квадратичного уравнения регрессии равно…
6. Линейное уравнение регрессии имеет вид
1. 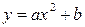 ;
;
2. 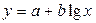 ;
;
3. 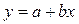 ;
;
4. 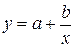 .
.
7. Тесноту связи изучаемых явлений для линейной регрессии оценивает
1. средняя ошибка аппроксимации;
2. индекс корреляции;
3. среднее квадратическое отклонение;
4. коэффициент корреляции.
8. Значение индекса корреляции находится в промежутке
1. [-1;1];
2. [0;1];
3. [0;2];
4. [-2;2].
9. По 20 наблюдениям получены следующие данные: уравнение регрессии 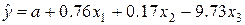 ,
, 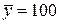 ,
, 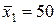 ,
, 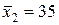 ,
, 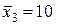 . Оцените параметр
. Оцените параметр 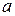 .
.
10. По 15 территориям России исследуется зависимость среднедневного душевого дохода ( 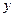 , руб.) от среднедневной заработной платы одного работающего (
, руб.) от среднедневной заработной платы одного работающего ( 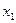 , руб.) и среднего возраста безработного (
, руб.) и среднего возраста безработного ( 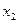 , лет). Рассчитаны коэффициенты парной корреляции
, лет). Рассчитаны коэффициенты парной корреляции 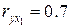 ,
, 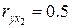 ,
, 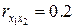 . Рассчитайте стандартизованные коэффициенты
. Рассчитайте стандартизованные коэффициенты 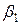 и
и 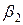 .
.
11. При изучении зависимости среднедневного душевого дохода ( 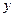 , руб.) от среднедневной заработной платы одного работающего (
, руб.) от среднедневной заработной платы одного работающего ( 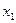 , руб.) и среднего возраста безработного (
, руб.) и среднего возраста безработного ( 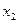 , лет) было получено следующее уравнение регрессии в стандартизованном масштабе
, лет) было получено следующее уравнение регрессии в стандартизованном масштабе 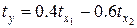 . Известно также, что
. Известно также, что 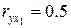 ,
, 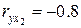 . Какова роль факторов неучтенных в модели (в %)?
. Какова роль факторов неучтенных в модели (в %)?
Вопросы для самоконтроля.
1. Что называется генеральной совокупностью, выборкой, реализацией выборки? Привести примеры.
2. Дайте определение дискретной и непрерывной случайных величин. Приведите примеры.
3. Что такое закон распределения случайной величины?
4. Что называется рядом распределения случайной величины?
5. Что такое функция распределения случайной величины? Какими свойствами она обладает?
6. Что называется функцией плотности распределения вероятностей случайной величины? Перечислите ее свойства.
7. Дайте определение плотности распределения вероятностей случайной величины, перечислите ее свойства.
8. Запишите функцию и плотность распределения для нормального, равномерного и экспоненциального законов.
9. Что называется математическим ожиданием непрерывной и дискретной случайных величин? Что оно характеризует? Какими свойствами оно обладает? Какие еще числовые характеристики случайных величин Вам известны?
10. Дайте определение дисперсии случайной величины, перечислите ее свойства. Что она характеризует?
11. Как определяются математическое ожидание и дисперсия для биномиального, равномерного, показательного, нормального распределений?
12. Что называется статистикой, оценкой неизвестного параметра?
13. Какая оценка называется состоятельной, несмещенной, эффективной?
14. Какие оценки математического ожидания и дисперсии генеральной совокупности Вы знаете?
15. Что такое интервальная оценка и чем она отличается от точечной?
16. Что такое статистическая гипотеза, нулевая, и альтернативная гипотезы? Какую гипотезу называют простой, сложной?
17. Что регрессионная зависимость?
18. Что такое корреляционное поле?
19. Запишите уравнение линейной регрессии.
20. Запишите уравнение квадратичной регрессии.
21. В чем заключается метод наименьших квадратов (МНК)?
22. Какие количественные характеристики степени зависимости случайных величин вам известны?
23. Как оценивается теснота связи между исследуемыми величинами?
24. Что такое коэффициент корреляции и как его найти?
25. Что такое коэффициент (индекс) детерминации и как его найти?
26. Как оценивается статистическая значимость и надежность уравнения регрессии?
31. Получить уравнение линейной регрессии, сделать чертеж
| xi | ||||||
| yi |
32. В чем коренное отличие дисперсионного анализа от регриссионного, а в чем сходство?
33. Выпишите формулы для общей и групповых выборочных средних, какая связь между ними?
34. Выпишите формулы для факторной и остаточной дисперсий, что каждая из них характеризует, какая связь между ними?
35. Какой критерий применяется при проверки гипотез методом однофакторного дисперсионного анализа, как определяются степени свободы? Как вычислить Fрасч?
36. Что вы знаете о двухфакторном дисперсионном анализе?
a) Как проверить гипотезу о влиянии каждого фактора на результирующий признак в двухфакторном анализе?
b) Как проверить гипотезу о влиянии на результирующий признак сочетания факторов?
c) Как найти оценку для дисперсии, обусловленной первым фактором?
d) Как найти оценку для дисперсии, обусловленной вторым фактором?
e) Как найти оценку для дисперсии, обусловленной взаимодействием 2х факторов для остаточной дисперсии?
f) Какие гипотезы можно проверять при помощи 2х факторного дисперсионного анализа? Как их проверить?
37. Современные статистические комплексы.
38. Пакет stats прикладного пакета программ MAPLE, применение для решения задач.
39. Работа со статистическими функциями в пакете MAPLE.
40. Статистические функции в пакете EXCEL, работа с ними.
41. Новые возможности специализированного пакета STATISTUKA
Варианты контрольных работ для самоконтроля знаний
Контрольная работа
Вариант 1.
- Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность того, что: а) только один снаряд попадет в цель, б) только два снаряда попадут в цель, в) все три снаряда попадут в цель, г) хотя бы один снаряд попадет в цель.
- Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что событие наступит 20 раз в 100 испытаниях.
- Найти закон распределения дискретной случайной величины
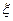 , которая имеет два возможных значения:
, которая имеет два возможных значения: 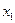 и
и 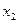 , причем
, причем 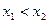 . Математическое ожидание
. Математическое ожидание 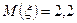 , дисперсия
, дисперсия 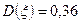 и вероятность
и вероятность 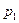 возможного значения
возможного значения 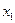 равна 0,9.
равна 0,9. - Случайная величина
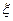 задана функцией распределения
задана функцией распределения 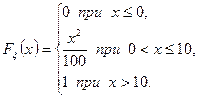
Требуется: а) найти плотность распределения вероятностей, б) найти математическое ожидание и дисперсию 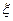 , в) построить графики функции распределения и плотности распределения вероятностей.
, в) построить графики функции распределения и плотности распределения вероятностей.
- Найти вероятность попадания в интервал
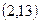 нормально распределенной случайной величины
нормально распределенной случайной величины 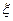 , если известны ее математическое ожидание
, если известны ее математическое ожидание 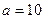 и среднее квадратическое отклонение
и среднее квадратическое отклонение 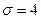 .
.
Вариант 2.
- Случайная величина
 задана функцией распределения
задана функцией распределения 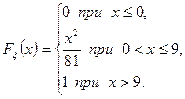
Требуется: а) найти плотность распределения вероятностей, б) найти математическое ожидание и дисперсию 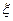 , в) построить графики функции распределения и плотности распределения вероятностей.
, в) построить графики функции распределения и плотности распределения вероятностей.
- Найти вероятность попадания в интервал
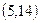 нормально распределенной случайной величины
нормально распределенной случайной величины 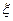 , если известны ее математическое ожидание
, если известны ее математическое ожидание 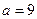 и среднее квадратическое отклонение
и среднее квадратическое отклонение 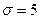 .
. - Задана матрица
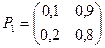 перехода системы из состояния
перехода системы из состояния 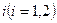 в состояние
в состояние 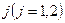 за один шаг. Найти матрицу
за один шаг. Найти матрицу 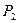 перехода системы из состояния
перехода системы из состояния 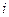 в состояние
в состояние 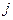 за два шага.
за два шага. - Найти: а) выборочную среднюю, б) выборочную дисперсию, в) выборочное среднее квадратическое отклонение для статистического распределения
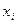 | |||||||
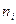 |
5. Найти доверительный интервал для оценки математического ожидания нормального распределения с надежностью 0,95, зная выборочную среднюю 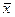 , объем выборки
, объем выборки 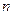 и среднее квадратическое отклонение
и среднее квадратическое отклонение 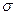 .
.
Варианты контрольных работ для текущей аттестации
Вариант № 1.
1. Все значения равномерно распределенной случайной величины лежат на отрезке 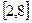 . Найти вероятность попадания случайной величины в промежуток
. Найти вероятность попадания случайной величины в промежуток 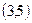 .
.
2. Случайная величина Х распределена по нормальному закону с математическим ожиданием 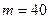 и дисперсией
и дисперсией 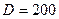 . Вычислить вероятность попадания случайной величины в интервал
. Вычислить вероятность попадания случайной величины в интервал 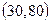 .
.
3. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения 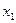 с известной вероятностью
с известной вероятностью 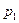 и
и 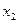 , причем
, причем 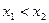 . P1 =0,1; М(Х)=1,9; D(Х)= 0,09.
. P1 =0,1; М(Х)=1,9; D(Х)= 0,09.
4. Найти математическое ожидание, корреляционную функцию и дисперсию случайной величины 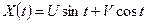 , где
, где 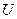 и
и 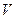 - некоррелированные случайные величины, причем М(U)=1, М(V)=2, D(U)=3, D(V)=4.
- некоррелированные случайные величины, причем М(U)=1, М(V)=2, D(U)=3, D(V)=4.
5. Найти корреляционную функцию стационарной случайной функции Х(t), зная ее спектральную плотность 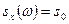 в интервале
в интервале 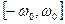 ; вне этого интервала
; вне этого интервала 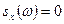 .
.
Вариант № 2.
1. Все значения равномерно распределенной случайной величины лежат на отрезке 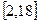 . Найти вероятность попадания случайной величины в промежуток
. Найти вероятность попадания случайной величины в промежуток 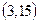 .
.
2. Случайная величина Х распределена по нормальному закону с математическим ожиданием 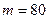 и дисперсией
и дисперсией 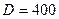 . Вычислить вероятность попадания случайной величины в интервал
. Вычислить вероятность попадания случайной величины в интервал 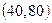 .
.
3. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения 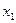 с известной вероятностью
с известной вероятностью 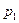 и
и 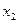 , причем
, причем 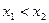 . P1 = 0,2; М(Х)=2,6; D(Х)= 0,64.
. P1 = 0,2; М(Х)=2,6; D(Х)= 0,64.
4. Найти математическое ожидание, корреляционную функцию и дисперсию случайной величины 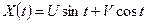 , где
, где 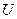 и
и 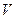 - некоррелированные случайные величины, причем М(U)=2, М(V)=3, D(U)=4, D(V)=4.
- некоррелированные случайные величины, причем М(U)=2, М(V)=3, D(U)=4, D(V)=4.
5. Найти корреляционную функцию стационарной случайной функции Х(t), зная ее спектральную плотность 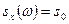 в интервале
в интервале 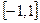 ; вне этого интервала
; вне этого интервала 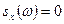 .
.
Вариант № 3.
1. Все значения равномерно распределенной случайной величины лежат на отрезке 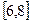 . Найти вероятность попадания случайной величины в промежуток
. Найти вероятность попадания случайной величины в промежуток 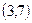 .
.
2. Случайная величина Х распределена по нормальному закону с математическим ожиданием 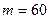 и дисперсией
и дисперсией 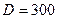 . Вычислить вероятность попадания случайной величины в интервал
. Вычислить вероятность попадания случайной величины в интервал 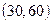 .
.
3. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения 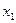 с известной вероятностью
с известной вероятностью 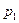 и
и 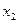 , причем
, причем 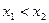 . P1 =0,3; М(Х)=3,1; D(Х)= 1,89.
. P1 =0,3; М(Х)=3,1; D(Х)= 1,89.
4. Найти математическое ожидание, корреляционную функцию и дисперсию случайной величины 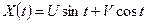 , где
, где 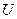 и
и 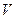 - некоррелированные случайные величины, причем М(U)=4, М(V)=5, D(U)=1, D(V)=3.
- некоррелированные случайные величины, причем М(U)=4, М(V)=5, D(U)=1, D(V)=3.
5. Найти корреляционную функцию стационарной случайной функции Х(t), зная ее спектральную плотность 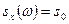 в интервале
в интервале 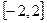 ; вне этого интервала
; вне этого интервала 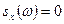 .
.
Вопросы и задачи для контроля остаточных знаний студентов
Контрольные вопросы
1. Что называется генеральной совокупностью, выборкой, реализацией выборки? Привести примеры.
2. Что называется рядом распределения случайной величины?
3. Что такое закон распределения случайной величины?
4. Дайте определение дискретной и непрерывной случайных величин. Приведите примеры.
5. Что такое функция распределения случайной величины? Какими свойствами она обладает?
6. Что называется функцией плотности распределения вероятностей случайной величины? Перечислите ее свойства.
7. Чем различаются графики функций распределения дискретной и непрерывной случайных величин?
8. Дайте определение плотности распределения вероятностей случайной величины, перечислите ее свойства.
9. Как построить сгруппированный и интервальный статистические ряды, гистограмму, эмпирическую функцию распределения?
10. Что называется математическим ожиданием непрерывной и дискретной случайных величин? Что оно характеризует? Какими свойствами оно обладает? Какие еще числовые характеристики случайных величин Вам известны?
11. Дайте определение дисперсии случайной величины, перечислите ее свойства. Что она характеризует?
12. Как определяются математическое ожидание и дисперсия для биномиального, равномерного, показательного, нормального распределений?
13. В чем заключается выборочный метод построения математической модели эксперимента?
14. Что называется эмпирической функцией распределения? Какими свойствами она обладает?
15. В чем состоит отличие эмпирической функции распределения от теоретической?
16. Как построить гистограмму относительных частот?
17. Что называется статистикой, оценкой неизвестного параметра?
18. Какая оценка называется состоятельной, несмещенной, эффективной?
19. Какие оценки математического ожидания и дисперсии генеральной совокупности Вы знаете?
20. Что такое интервальная оценка и чем она отличается от точечной?
21. Что такое статистическая гипотеза, нулевая, и альтернативная гипотезы? Какую гипотезу называют простой, сложной?
22. Дайте определение статистического критерия.
23. Что такое ошибки первого и второго рода?
24. Какую гипотезу Вы проверяете в этой работе? На какой статистике строится соответствующий критерий?
25. Как найти число степеней свободы?
26. Какой смысл имеет уровень значимости критерия?
27. Опишите подробно критерий Пирсона.
