Метод бисекции и простой итерации решения уравнений с одним неизвестным
Ур. с одним неизвест. имеет след. общий вид 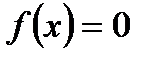 ,(1), где
,(1), где 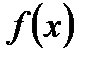 – ф., заданная на всей числовой оси или на конечном ее отр.
– ф., заданная на всей числовой оси или на конечном ее отр.
Теорема. Если ф. 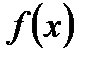 непрерывна на
непрерывна на 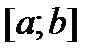 и принимает на концах этого отр. знач. разных знаков, то ур. (1) имеет внутри отр. хотя бы один корень.
и принимает на концах этого отр. знач. разных знаков, то ур. (1) имеет внутри отр. хотя бы один корень.
Док. Обозначим 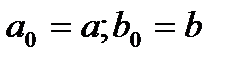 . Пусть построены отр.
. Пусть построены отр. 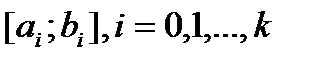 , удовл. усл.1)
, удовл. усл.1) 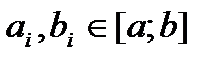 ; 2)
; 2) 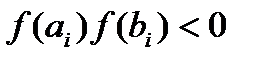 ;
;
3) 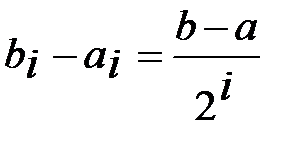 .
.
Рассм. построение очередного отр. 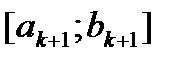 Найдем середину отр.
Найдем середину отр. 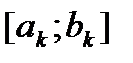 :
:  (2) и вычислим
(2) и вычислим 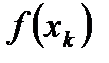 . Если
. Если 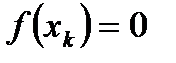 , то утвержд. теоремы справедливо.
, то утвержд. теоремы справедливо.
Пусть 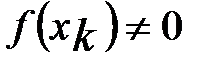 . Положим
. Положим 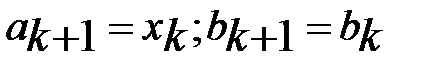 , если
, если 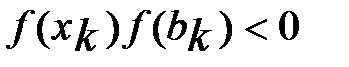 и
и 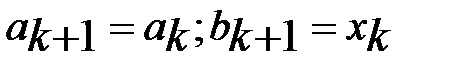 в противном случае. Очевидно выполнение равенства
в противном случае. Очевидно выполнение равенства 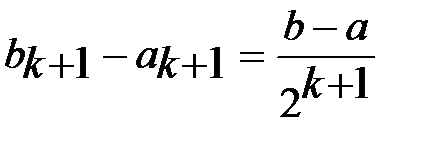 (3). Т.к. последов.
(3). Т.к. последов. 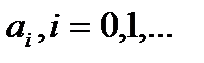 не убывает и ограничена сверху, то она имеет предел
не убывает и ограничена сверху, то она имеет предел 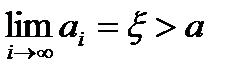 . Из (3) следует, что и
. Из (3) следует, что и 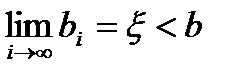 . Поскольку
. Поскольку 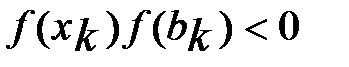 , то
, то 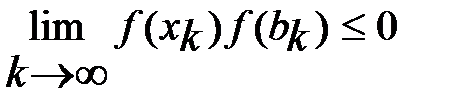 . Отсюда и из непрерывности ф. получаем
. Отсюда и из непрерывности ф. получаем 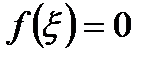 . Теорема доказана.
. Теорема доказана.
Метод решения ур. (1), построенный при док-ве теоремы наз. методом бисекции или методом половинного деления отр.
Метод простой итерации.
Пусть на 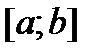 задано ур. в виде
задано ур. в виде 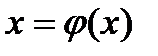 . (4)
. (4)
Метод простой итерации для ур. (4) имеет расчетную форм. 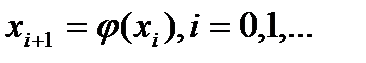 . (5)
. (5)
Теорема. Пусть ур. (4) имеет корень 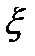 и существует такое
и существует такое 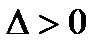 , что на отр.
, что на отр. 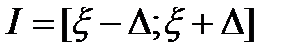 производная ф.
производная ф. 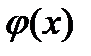 существует, непрерывна и по модулю строго меньше единицы:
существует, непрерывна и по модулю строго меньше единицы: 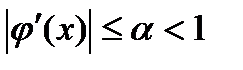 . Тогда метод простой итерации (5) сходится при
. Тогда метод простой итерации (5) сходится при 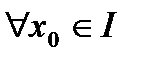 .
.
Методы хорд и касательных как частные случаи метода простой итерации.
Квадратический характер сходимости метода касательных (Ньютона). Пусть на 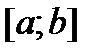 задано ур. в виде
задано ур. в виде 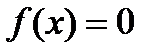 . (1) Будем считать, что на
. (1) Будем считать, что на 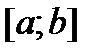 ур. (1) имеет корень
ур. (1) имеет корень 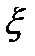 и производные
и производные 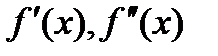 непрерывны на отр. и сохраняют знак. Введем в рассм. ф.
непрерывны на отр. и сохраняют знак. Введем в рассм. ф. 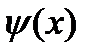 , кот. непрер. на
, кот. непрер. на 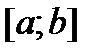 и не обращ. на нем в нуль. При этих усл. ур.
и не обращ. на нем в нуль. При этих усл. ур. 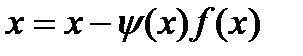 (2) будет равносильно на
(2) будет равносильно на  ур. (1). Ур. (2) имеет вид
ур. (1). Ур. (2) имеет вид 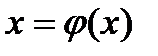 , где
, где 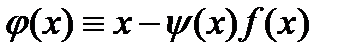 . Возьмем
. Возьмем 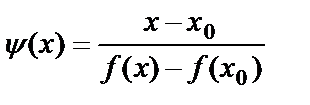 . Тогда ур. (2) приобретает вид
. Тогда ур. (2) приобретает вид 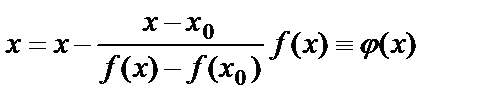 . (3)
. (3)
Запишем расчетные форм. метода простой итерации для ур. (3) 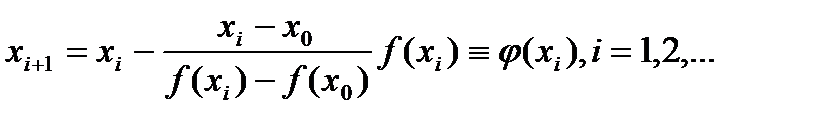 . (4)
. (4)
Построенный метод решения ур. (1) с расчетными форм. (4) наз. методом хорд.
Исследуем сходимость метода хорд. Проводя дифф. в (3), получаем 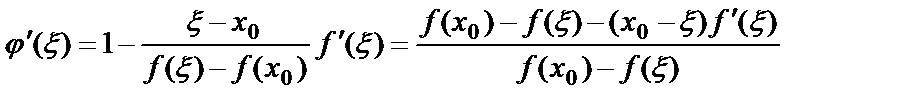 . (5) Используя разложение в ряд Тейлора, имеем
. (5) Используя разложение в ряд Тейлора, имеем 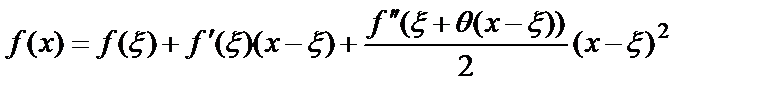 . Положив в последнем равенстве
. Положив в последнем равенстве 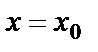 , выразим остаточ. член форм. Тейлора. После подстановки в (5) и применении к знаменателю в (5) формулу конечных приращений Лагранжа, получим
, выразим остаточ. член форм. Тейлора. После подстановки в (5) и применении к знаменателю в (5) формулу конечных приращений Лагранжа, получим
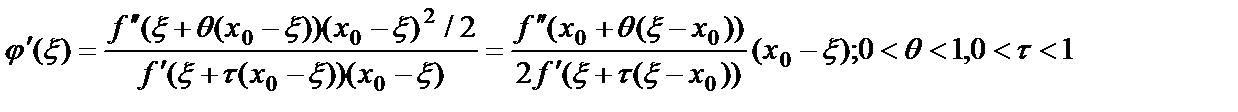 .
.
Отсюда имеем оценку 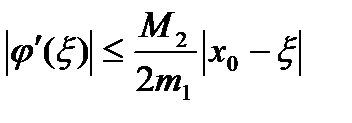 , (6), где
, (6), где 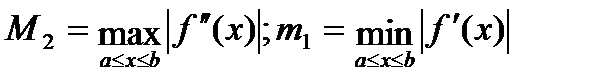 . Оценка (6) показывает, что если взять
. Оценка (6) показывает, что если взять 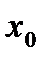 достаточно близким к корню
достаточно близким к корню 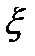 , то будет выполняться неравенство
, то будет выполняться неравенство 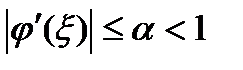 . В силу непрерывности производной, существует
. В силу непрерывности производной, существует  - окр. точки
- окр. точки 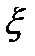 отр.
отр. 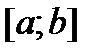 , где выполняются усл. теоремы о сходимости метода простой итерации.
, где выполняются усл. теоремы о сходимости метода простой итерации.
Возьмем теперь 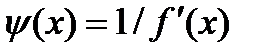 . Тогда ур. (2) приобретает вид
. Тогда ур. (2) приобретает вид 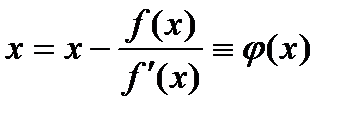 . (7)
. (7)
Запишем расчетные форм. метода простой итерации для ур. (7) 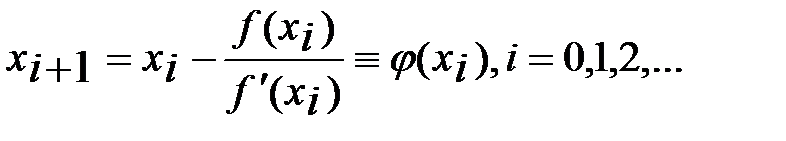 (8)
(8)
Построен. метод решения ур. с расчетными ф-ми (8) наз. методом Ньютона (касательных). Исследуем сх-ть метода Ньютона. Проводя диф-е в (7) получаем 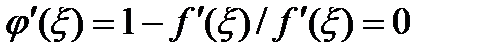 . Метод Ньютона имеет квадратич. хар-р сх-ти. Действительно, из (8) имеем
. Метод Ньютона имеет квадратич. хар-р сх-ти. Действительно, из (8) имеем 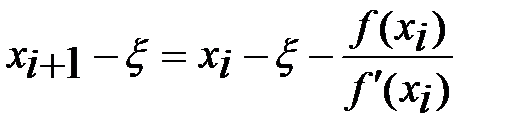 . (9) Используя разложение в ряд Тэйлора
. (9) Используя разложение в ряд Тэйлора 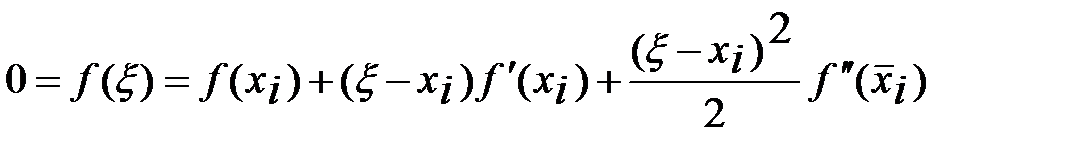 находим
находим 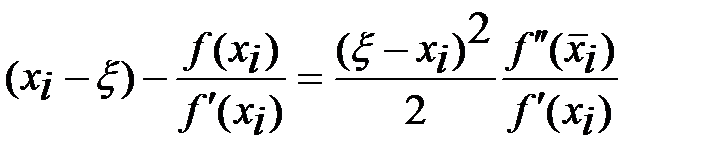 . Заменяя в (9) правую часть полученным выражением, приходим к формуле
. Заменяя в (9) правую часть полученным выражением, приходим к формуле 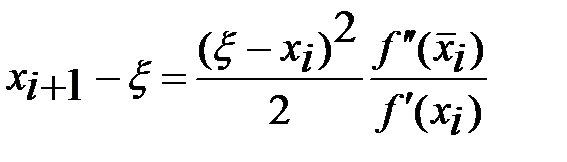 и оценке
и оценке 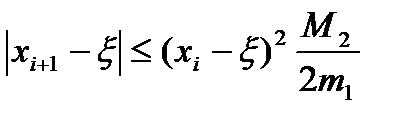 , где
, где 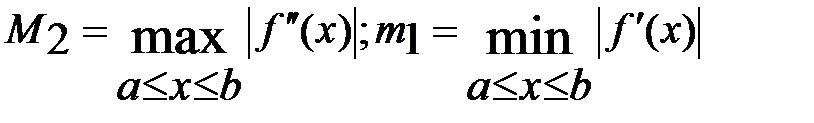 .
.
