Интервальная оценка индивидуального значения зависимой переменной

Одной из основных задач эконометрического анализа является прогнозирование значений зависимой переменной при определенных значениях Хпр объясненной переменной.

Предположим, что мы построили некое эмпирическое значение парной регрессии ỹ_i=b₀+b₁x_i, на основе кот-го хотим предсказать среднюю величину зависимой переменной у при х=х_пр. В данном случае рассчитанное по уравнению величина ỹ_пр=b₀+b₁x_пр является только оценкой для искомого матожидания.

Встает вопрос насколько эта оценка отклоняется от среднего матожидания для того, чтобы ей можно было доверять с надежностью γ=1-α.

Чтобы построить доверит интервал, покажем, что случайная величина ỹ_пр имеет норм распределение с некоторыми конкретными переменными.

Мы знаем, что ỹ_пр=b₀+b₁x_пр. Подставим в это уравнение значение для bo и b1, найденное в виде лин комбинаций выборочных величин объясняющей переменной yi.

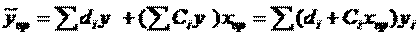
Т.е. расчетная величина действительного имеет норм распред-ие и мы находим матожидание и дисперсию.

М(Ỹпр)=M(bo+b1Xпр)= βo+Xпрβ1

D(Ỹпр)=D(bo+b1Xпр) = D(bo)+X²прM(b1)=2cov(bo,b1Xпр)***=

Рас-м вел-ну ковариации.

Заменим вел-ну bo ч/з правило ее вычисления из эмпир ур-ия регр-ии, аналог-но поступим со знач-ем βо, записав его знач-ие ч/з теорет ур-ие регр-ии.

Тогда получаем

-

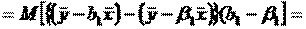
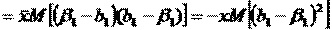это дисп-ия для значения b1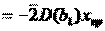

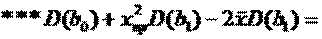
Мы знаем вел-ну дисп bo и b1. Подставим сюда их значения:

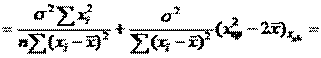
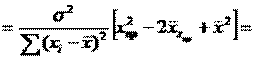
Преобразуем данное выр-ие прибавив и отняв к скобке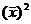

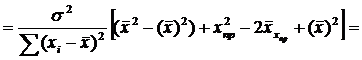
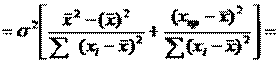
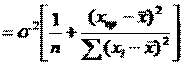
В этом выр-ии заменяем σ² несмещенной оценкой по эмпир ур-ию регр-ии σ²=∑ei²/n-2 и тогда мы м рассчитать Т стат-ку

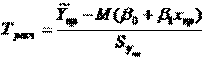
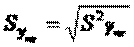, получаемого из значения теорет дисп-ии заменой дисп теорет откл-ия σ² на So², вычис-ое по выборке ∑ei²/n-2. Используя табл. Стьюдента, можем вычесть вероятность того, что |T|≤tрасч

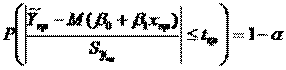
Тогда ν=n-2.

Таким образом, сделав такие же преобразования как для коэффициентов в уравнения, получаем, что

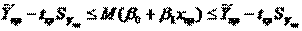
Классическая парная регрессионная модель. Спецификация модели.

Спецификация парной линейной регр. модели имеет вид: Y=a+bX+ε, где a и b – параметры модели (постоянные неизвестные коэфф-ты), Х – экзогенная переменная (регрессор), У – эндогенная переменная (отклик), ε – случайное возмущение, характеризующее отклонение f(x)= a+bX (теоретической линей зависимости) и возникающее:

- из-за ошибок спецификации

- из-за ошибок измерений

Уравнения для отдельных наблюдений зависимой переменной У записываются в виде (схема Гаусса-Маркова)

Y_t=a+bX_t+ε_t , t=1,…,n – выборочные данные, n – объём выборки.

Относительно возмущений ε_t, в регр.моделях принимаются след. предположения (условия Гаусса-Маркова)