Вынужденные колебания. Резонанс

До сих пор мы рассматривали колебательное движение тела так, как если бы оно происходило совершенно беспрепятственно. Однако если движение происходит в какой-либо среде, то эта среда оказывает сопротивление движению, стремясь замедлить его. Процесс взаимодействия тела со средой можно описать введением силы сопротивления, направленной в сторону, противоположную скорости движения тела. При достаточно малых скоростях движения (что, в принципе, может быть обусловлено малостью смещения) сила сопротивления пропорциональна скорости тела

F_сопр = -rv (56)

где r – положительная постоянная (коэффициент сопротивления), характеризующая взаимодействие тела со средой. Трение, описываемое формулой (56) часто называют «колебательным трением».

Выясним, как влияет наличие такого взаимодействия на колебательное движение. Будем считать при этом, что сила сопротивления настолько мала, что вызываемая ею потеря энергии ΔE за время одного периода колебаний T относительно мала, т.е.

ΔЕ/Е << 1. (57)

Потеря энергии ΔE равна работе силы сопротивления

ΔE = <F_сопр> ΔS = r <v²> T = -2 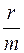< 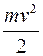> T , (58)

где < 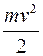> - среднее значение (за период колебаний) кинетической энергии, равное половине полной энергии колебаний

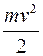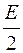< > = . (59)

Подставив (58) в (57), получим

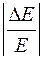= - 2βТ = - ,

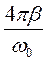где β = r/2m - коэффициент затухания.

Можно показать, что при наличии силы сопротивления (56) полная энергия системы убывает со временем по закону

E = E₀ e^-2βt , (60)

где E₀ - значение энергии в начальный момент времени.

Во всякой реальной колебательной системе всегда происходят те или иные процессы трения. Поэтому свободные колебания, возникающие в системе, с течением времени затухают. Для того чтобы возбудить незатухающие колебания, необходимо компенсировать потери энергии, обусловленные трением. Такая компенсация может производиться внешними (по отношению к колебательной системе) источниками энергии. Простейшим случаем является воздействие на систему переменной внешней силы 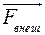, изменяющейся со временем по гармоническому закону

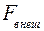= F₀ cos ωt (61)

с некоторой частотой ω. Под влиянием этой силы в системе возникнут колебания, происходящие в такт с изменением внешней силы; эти колебания называются вынужденными.

Второй закон Ньютона для движения осциллятора под действием указанных сил имеет вид

ma = - kx – rv + F₀ cos ωt . (62)

Незатухающие колебания происходят с частотой внешней силы и представляются в виде

x(t) = A cos (ωt - φ) (63)

где A – амплитуда, а φ – некоторый сдвиг по фазе между вынуждающей силой и вызываемыми ею колебаниями.

Можно показать, что амплитуда вынужденных колебаний зависит от амплитуды внешней силы F₀ , от частоты собственных колебаний системы ω₀, откоэффициента затухания β и, конечно, от частоты внешней силы ω. На рис.15 представлен график зависимости амплитуды от частоты вынуждающей силы ω при малом затухании β. Если коэффициент затухания мал (по сравнению с собственной частотой), то наибольшего значения амплитуда колебаний достигает приблизительно при совпадении частот, или, как говорят, при резонансе. При ω = ω₀ максимальное значение

А_max = 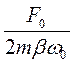(64)

обратно пропорционально коэффициенту затухания. По этой причине при резонансе нельзя пренебрегать трением в системе, даже если оно мало. Кривая на рис. 15 называется резонансной кривой.

Сравним значение А_max со смещением А_ст, которое испытало бы тело под действием постоянной (статической) силы, равной F₀ . Смещение А_ст можно найти из общей формулы (63) для амплитуды, положив в ней ω = 0 (при ω = 0 сила 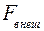= F₀ cos ωt = F₀)

А_ст = 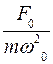(65)

Отношение резонансного смещения к статическому равно

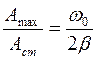(66)

Мы видим, что относительное увеличение амплитуды колебаний при резонансе (по сравнению со статическим отклонением) определяется отношением частоты собственных колебаний к коэффициенту затухания. Для систем с малым затуханием это отношение может быть очень большим. Это обстоятельство разъясняет огромное значение явления резонанса в физике и технике: им широко пользуются, если хотят усилить колебания, и всячески избегают, если резонанс может привести к нежелательному росту колебаний.

В авиации примером вынужденных колебаний является бафтинг (buffet – удар, тряска). Это колебания оперения самолета, вызванные воздействием завихренного потока воздуха. Источником вихрей служит срыв потока с крыла на больших углах атаки, срыв потока в местах сопряжения крыла и фюзеляжа, на фонаре кабины, на пилонах подвески двигателей, на гондолах двигателей, расположенных на крыле, на наружной подвеске вооружения или топливных баков.

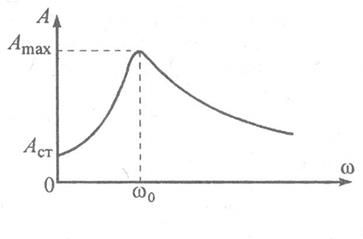
Рис.15. Примерный вид резонансной кривой и характерные точки на ней (А_ст – смещение под действием амплитуды внешней силы, А_max – максимальное смещение при резонансе, ω₀ – собственная частота, близкая к резонансной)

Для установления резонанса необходимо:

- действие периодической силы на осциллятор с достаточно малым затуханием (ω₀ > β);

- резонанс устанавливается после того, как закончился переходной процесс;

- частота внешней периодической силы близка к (или равна) собственной частоте осциллятора (в зависимости от вида резонанса (см. ниже)).