Строго периодическое восстановление

Согласно этой стратегии система восстанавливается после отказа. Если она проработала без отказов заданный интервал времени τ, то проводится профилактическая замена (рис.4.8). Восстановления, которые производятся после отказов, называются аварийными. Как профилактические, так и аварийные восстановления являются полными.

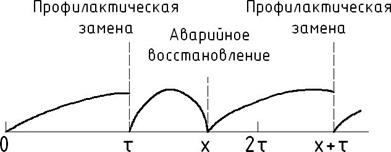
Рис.4.8 Строго периодическое восстановление

Пусть ξ_τ и η_τ — случайные времена соответственно между двумя последовательными аварийными восстановлениями и двумя последовательными восстановлениями произвольного типа. Тогда

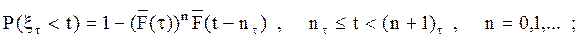
где

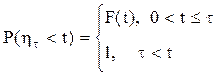(4.38)

Если обозначить 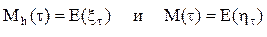, то

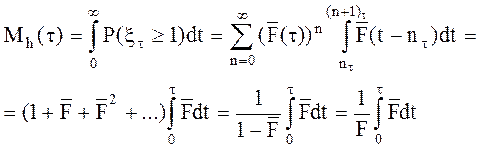
Таким образом

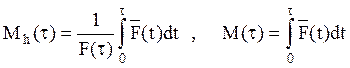
Моменты, в которые производятся аварийные восстановления, профилактические восстановления или восстановления произвольного типа, задают, согласно определению, процессы восстановления. Если обозначим через M_P(τ) математическое ожидание времени между двумя профилактиками, то 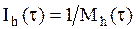, 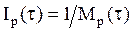и 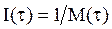будут означать среднее число соответственно аварийных восстановлений, профилактик и восстановлений произвольного типа в единицу времени.

Очевидно

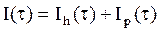(3.5)

Отсюда следует:

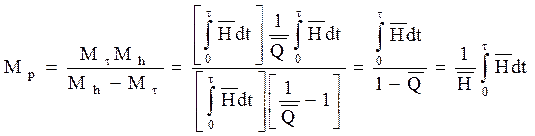
где ,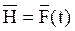

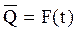
Отсюда

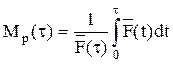
Оценка ИНТЕНСИВНОСТи ЭКСПЛУАТАЦИОННЫХ ЗАТРАТ.

Пусть c_h и c_p – средние затраты на аварийное и профилактическое восстановление соответственно, 0 < c_p < c_h < ¥. Если интервал восстановления равен τ, то интенсивность эксплуатационных затрат

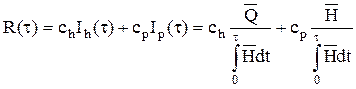
или

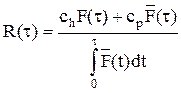
Отсюда :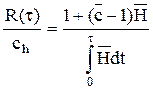

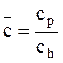
Из условия оптимальности: 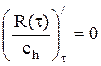, следует

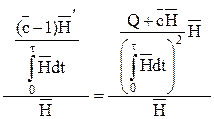
После преобразований имеем

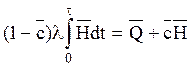
или

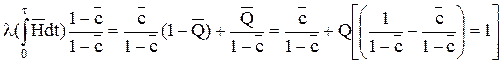
Отсюда

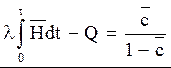(4.39)

Оценка оптимальной интенсивности затрат

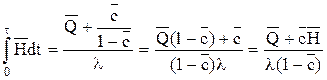
Отсюда

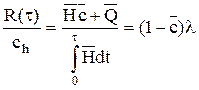
Таким образом

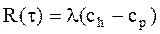
Пример: Пусть 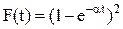, 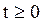. Соответствующая интенсивность отказов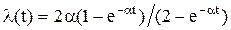

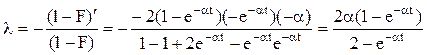
и 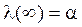, справедлива оценка 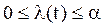. Из уравнения (4.39) получается уравнение для определения оптимального τ = τ* :

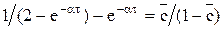
Действительно

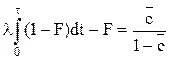
где

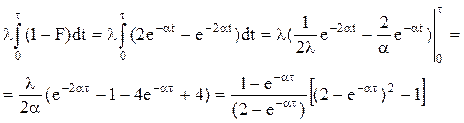
Отсюда

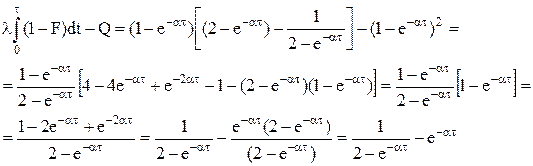
Таким образом

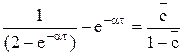
Решение τ* этого квадратного уравнения (после подстановки 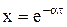) существует тогда и только тогда, когда :

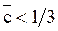В дальнейшем введем замену .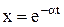

Тогда уравнение примет вид

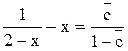или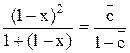

Введя замену U = 1 – x , получим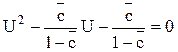

Решая уравнение, найдем

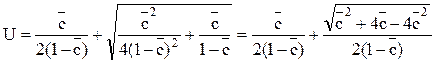
Отсюда

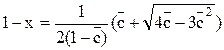
или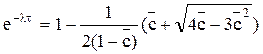

Разрешая уравнение относительно τ, найдем

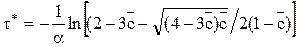
Принимая 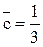получим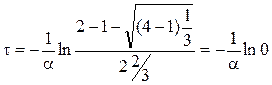

Таким образом для 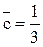оказывается, что 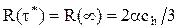. Это – интенсивность производственных затрат, которая получается при стратегии аварийных замен.

В дальнейшем предположим , что аварийное и профилактическое восстановления требуют .времени, равного соответственно d_h и d_p,( 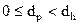.) В этом случае первостепенный Очевидно интервалы времени Y, на которых система восстанавливается, определяются соотношением

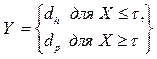
Отсюда следует

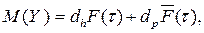
так что коэффициент готовности системы K(τ) задается в виде

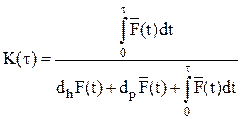
Задача состоит в максимизации коэффициента готовности К(τ) надлежащим выбором интервала восстановления τ. Поскольку, однако, величины 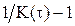и R(τ) имеют одинаковый функциональный вид, оптимизационные задачи «минимизации R(τ)» и «максимизация К(τ)» эквивалентны. Вследствие этого оптимальное относительно К(τ) значение τ = τ* вновь является решением уравнения (4/39), если подставить в него .

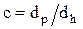Очевидно оптимальная периодичность будет удовлетворять условию оптимальности

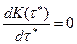
В дальнейшем получим приближенное решение для случая , когда время безотказной работы подчиняется распределению Вейбулла. Для высоконадежных систем приближенно можно принять

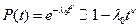
С учетом введенных упрощений уравнение оптимальности примет вид

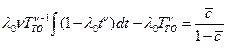
После преобразований получим

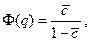
где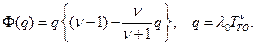

Характер зависимости 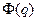представлен на рис. 4.9.

Пример. Принимая 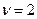, 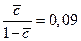по графику получим 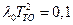. Таким образом периодичность обслуживания, при значении 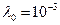, будет равна

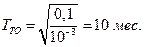
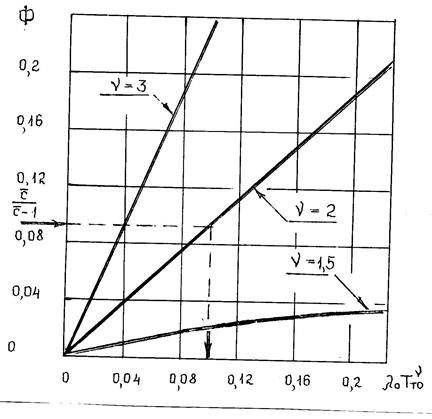
Рис. 4.9 Зависимость параметра 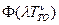для различных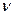

Стратегия замен через плановые промежутки времени.

В этом разделе обсуждается стратегия восстановления, при которой моменты осуществления профилактик установлены заранее. Эти стратегии особенно пригодны, когда профилактики требуют основательной подготовки или сопряжены со значительными затратами, как, например, при комплексном ремонте большого технического объекта или сложного электронного оборудования.

В случае отказа система подвергается аварийномy восстановлению. Независимо от возраста системы, в фиксированные моменты времени τ, 2τ, ... планомерно проводятся профилактики (рис.4.10).

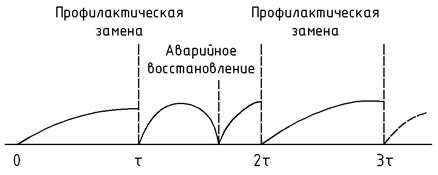
Рис.4.10. Восстановление через плановые интервалы времени

Пусть аварийные и профилактические (планомерные) восстановления проводятся полностью и требуют затрат соответственно b_h и b_p, 0 < b_p < b_h . Процесс функционирования системы разбивается на стохастически эквивалентные циклы [nτ, (n + 1)τ], n = 0, 1, … . Средние эксплуатационные затраты на цикл составляют E(C) = b_p + b_hH(τ) , где Н (τ) означает математическое ожидание числа аварийных восстановлений (отказов), происшедших на интервале (0, τ) . Функция восстановления Н (τ) соответствует F(t) и поэтому удовлетворяет уравнению восстановления (4.13).

Отсюда интенсивность эксплуатационных затрат

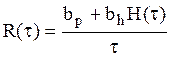
Оптимальный интервал восстановления τ = τ^* удовлетворяет уравнению ,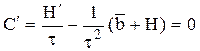

то есть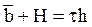

Таким образом

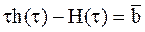, (4.40)

где 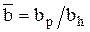, 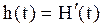есть плотность восстановления. Если интервал τ^* существует, то минимальная интенсивность эксплуатационных затрат

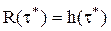
Для постоянной интенсивности отказов 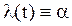выполняется соотношение 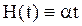, и уравнение (4.40) в этом случае не имеет конечного решения.

Пример: Пусть 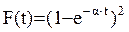, 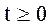. Преобразование Лапласа соответствующей плотности 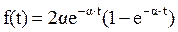имеет вид

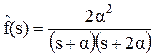
Принимая во внимание выражение 4.13, получаем преобразование Лапласа соответствующей плотности восстановления:

.

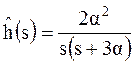Как видно из таблицы 4.3 ..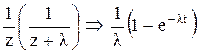

Отсюда принимая 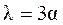, получим

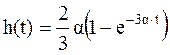
Интегрированием выражения h(t) получаем функцию восстановления

.

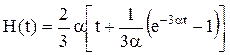Подстановка выражений h(t) и H(t) в (4.40) приводит к уравнению для оптимального интервала восстановления τ^*:

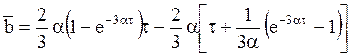
Производя преобразования, получим

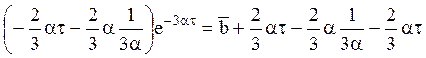
Отсюда

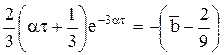
Таким образом

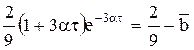
Окончательно

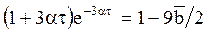
Однозначное решение существует, если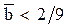

Для диапазона 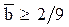более выгодной с точки зрения затрат является стратегия аварийных замен. Результаты расчета представлены на рис.4.11.

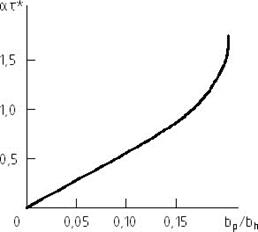
Рис. 4.11 Оптимальные интервалы восстановления

Недостаток рассмотренной стратегии (с точки зрения практических приложений состоит в том, что иногда профилактическому восстановлению подвергаются вполне «новые» системы (хотя при b_p<<b_h использование оптимального интервала восстановления τ^* в значительной степени исключает отказы системы на интервале (0, τ^*)). Поэтому проанализируем еще вариант, в котором этот недостаток устранен введением «зон бездействия». В дальнейшем предположим, что между двумя профилактиками не производится никаких мероприятий по восстановлению, а после отказов система восстанавливается только при следующем запланированном восстановлении (рис.4.12).

Если отказ системы наступил в момент x, где 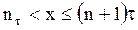, n = 0, 1, … , то система в течение времени 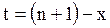остается неработоспособной.

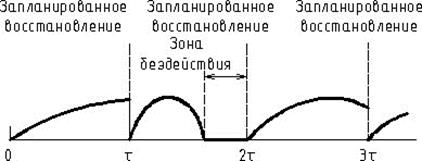
Рис.4.12 Восстановление с зонами бездействия

В этом случае для проведения анализа можно воспользоваться методом графов. Граф состояний анализируемой модели ТО представлен на рис. 4.13 .

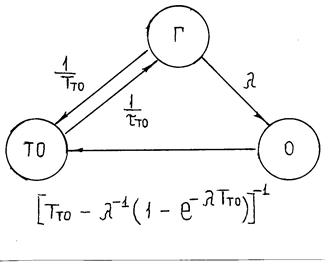
Рис. 4.13 Граф состояний системы.

В общем случае интенсивность перехода из состояния О в состояние ТО будет равна

,

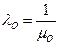где 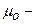среднее время нахождения системы в состоянии отказа.

Очевидно ,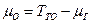

где 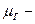среднее время нахождения системы в состоянии готовности в течении одного цикла.

С другой стороны 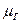можно рассматривать как математическое ожидание времени 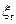между заменами произвольного типа

,

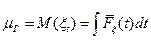где 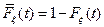, 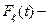функция распределения времени между заменами произвольного типа( см. рис. 4.14 )

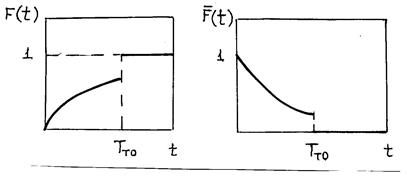
Рис. 4.14 Функция распределения 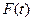и функция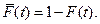

В рассматриваемом случае 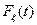будет равна

,

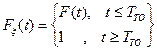где F(t) - функция распределения времени безотказной работы системы.

Для экспоненциального закона распределения получим

.

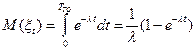Таким образом

.

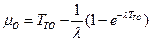Соответственно интенсивность перехода будет равна

.

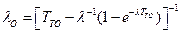Согласно графу вероятности нахождения системы в различных состояниях будут удовлетворять системе дифференциальных уравнений Колмогорова

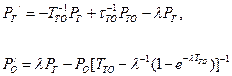
В стационарном режиме получим

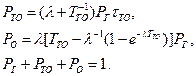
Разрешая систему относительно 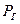, получим

.

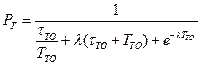В рассматриваемом случае периодичность РТО можно найти аналитически.

Очевидно оптимальные значения 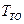должны удовлетворять условию

оптимальности

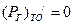, где .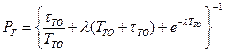

Принимая 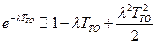, получим

.

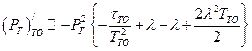Отсюда .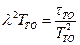

После преобразований окончательно получим .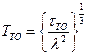

При произвольном законе распределения времени безотказной работы выражение для коэффициента готовности можно представить в виде

,

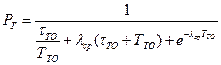где 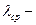средняя интенсивность отказа на отрезке .

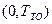Разлагая экспоненту в ряд и ограничиваясь квадратичным приближением, приближенно получим

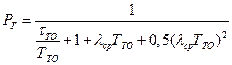
В случае « горячего резерва» вероятность отказа резервной группы на интервале ( 0, 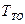) приближенно, для высоконадежных систем, можно оценить по соотношению

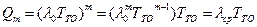, где .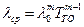

В этом случае выражение для 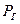примет вид

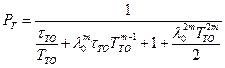
Оптимальная периодичность замен 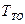будет удовлетворять условию оптимальности

.

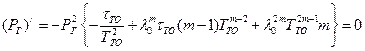Отсюда

.

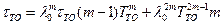После преобразований получим

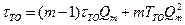
Разрешая соотношение относительно 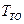, получим

.

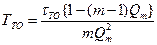Для высоконадежных систем, учитывая малость 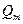, приближенно получим

.

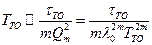Отсюда

.

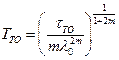Подставляя полученное соотношение в выражение для 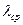, будем иметь

.

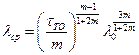Соответственно для 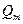найдем

.

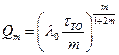Таким образом с уменьшением 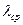периодичность замен будет расти . Однако снижение 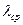потребует дополнительных материальных затрат. В общем случае суммарные затраты можно представить в виде

,

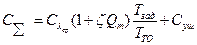где потери эффективности, обусловленные простоем;

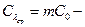стоимость проведения плановых замен;

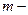кратность резерва ; ;

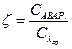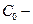стоимость элемента с интенсивностью отказа ;

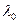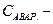стоимость восстановления системы при аварийном отказе.

В дальнейшем оценим оптимальную кратность ресурса m, обеспечивающую минимум суммарных затрат. При решении задачи воспользуемся оценкой периодичности замен, полученной ранее из условия обеспечения максимального коэффициента готовности.

Тогда выражение для суммарных затрат будет равно

,

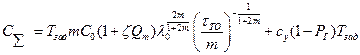где 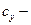удельные затраты, обусловленные простоем при отказах.

Переходя к безразмерным затратам, получим

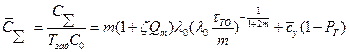, где .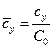

Раскрывая выражение для 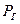и подставляя в него соотношение для 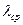, будем иметь

.

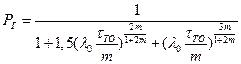Таким образом, окончательно, безразмерные затраты можно представить в виде

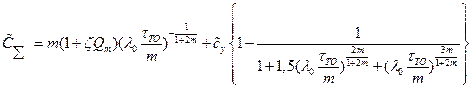
где ; .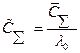

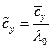Оптимальное значение m можно найти численно, перебором по m для заданных значений параметров 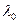, 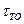и .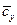

Вероятность безотказной работы резервной группы 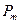, соответствующая оптимальной кратности резерва 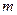, будет оцениваться по соотношению

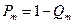, где .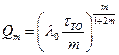

Пример.

Для иллюстрации работоспособности метода рассмотрим модельный пример. При проведении расчетов примем:

.

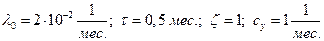Характер зависимости 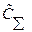от 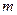представлен на рис. 4.15.

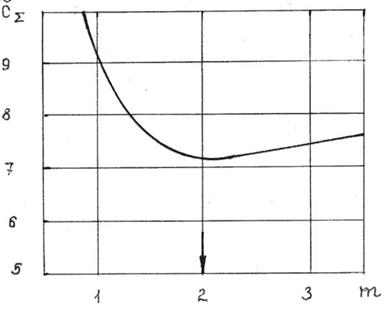
Рис. 4.15 Зависимость безразмерных затрат от кратности резерва.

Как видно из графика оптимальную кратность резерва можно принять равной двум.

Для других параметров соответственно получим:

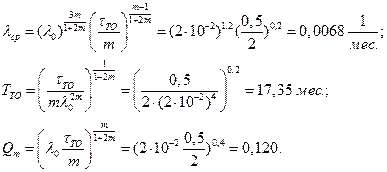
Метод графов, рассмотренный выше, может быть использован также для анализа стратегии плановых замен . Граф состояний системы , соответствующий рассматриваемой стратегии ТО , представлен на рис. 4.16 .

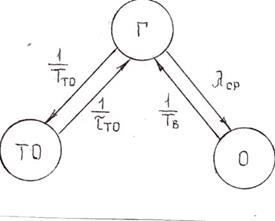
Рис. 4.16 Граф состояний системы

В стационарном режиме приходим к системе алгебраических уравнений

,

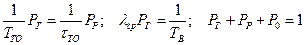Для высоконадежных систем среднюю интенсивность отказа приближенно можно оценить по соотношению

,

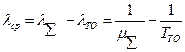где 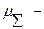среднее время между отказами произвольного типа

В случае распределения Вейбулла величина 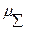может быть оценена по соотношению

.

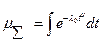Для высоконадежных систем, в виду малости 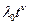, можно воспользоваться линейным приближением

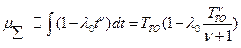
Отсюда

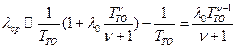
Подставляя значения 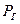и 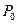в условие нормировки, получим

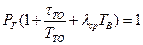
Очевидно максимум 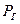будет достигаться при минимизации выражения

.

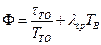С учетом выражения для 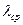условие оптимальности примет вид

.

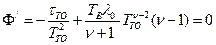Разрешая уравнение относительно 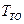, получим

.

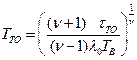Очевидно полученное решение соответствует минимуму удельных затрат.

Действительно в рассматриваемом случае выражение для коэффициента

готовности можно представить в виде

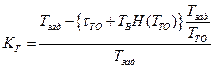
После преобразований получим

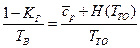, где .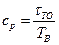

Полученное соотношение совпадает с критерием удельных затрат. Таким образом при оптимальном значении 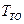, обеспечивающем максимум коэффициента готовности, будет достигаться минимум удельных затрат.