Гирокомпас на неподвижном основании

Для изучения гирокомпаса с косвенным управлением можно воспользоваться уравнениями движения обычного одногироскопного компаса соответственно, заменив в них моменты внешних сил.

Вместо момента силы тяжести гидравлического маятника и демпфирующего момента, создаваемого смещением центра тяжести чувствительного элемента, в рассматриваемом случае необходимо учесть торсионные моменты по осям прецессии гироскопа. Эти моменты» очевидно, пропорциональны углам закручивания торсионов по азимуту и высоте. Обозначим угол кручения по азимуту 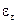и по высоте - .

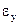Тогда для случая неподвижного основания мы можем записать уравнения движения гирокомпаса в следующем виде [3]:

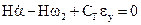
(3.1)

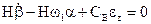
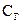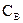где и - удельные моменты кручения пары торсионов соответственно горизонтальной и вертикальной.

Величины 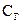и 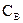характеризуют жесткость торсионов. Будем полагать, что следящие системы гирокомпаса работают со столь малыми постоянными времени (по сравнению с периодом собственных колебаний гирокомпаса), что инерционностью следящих систем можно пренебречь.

В таком случае величины углов кручения торсионов 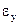и 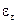зависят только от напряжения сигналов, поступающих на двигатели стабилизации от индикатора горизонта и от вычислительного устройства гирокомпаса.

Поэтому к уравнениям (3.1) остается добавить уравнение индикатора горизонта.

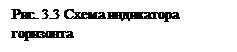Принципиальная схема индикатора горизонта показана на рис. 3.3. Основной его деталью является чувствительный элемент 1, представляющий собой тело, погруженное в вязкую жидкость 5 и растянутое с помощью пружин 6 вдоль некоторой оси XX, называемой осью чувствительности индикатора горизонта. Перемещение чувствительного элемента вдоль оси чувствительности измеряется с помощью индукционного съемного устройства (сигнального трансформатора 4 и якоря 2). Все эти элементы заключены в герметичный корпус 3. На рис. 3.3 показаны также ограничители 7, назначение которых будет понятно из дальнейшего. Индикатор горизонта устанавливается на следящей сфере так, что его ось чувствительности направлена параллельно оси ОХ собственного вращения гироскопа. Как видно из схемы рис. 3.3, сигнал индикатора горизонта при линейной характеристике съемного устройства пропорционален перемещению чувствительного элемента индикатора горизонта вдоль этой оси. Обозначим величину этого перемещения через 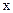. При наклонении следящей сферы вместе с гиросферой на чувствительный элемент индикатора горизонта действуют: проекция силы тяжести 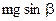, восстанавливающая сила упругости пружины 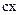и сила сопротивления жидкости 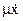. Здесь m — масса чувствительного элемента, 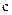- коэффициент упругости и 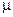- коэффициент сопротивления.

В соответствии с известным уравнением механики для малых углов 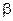имеем:

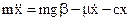(3.2)

или

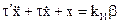(3.3)

где ; ;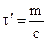

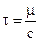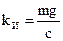
Величины 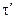и 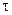являются постоянными времени индикатора горизонта. Постоянная времени 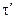вследствие малой массы чувствительного элемента и большой упругости пружин весьма мала, и ее можно не учитывать.

Поскольку величина 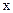электрически преобразуется в сигнал, управляющий двигателями стабилизации, мы можем написать (с учетом коррекции):

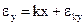
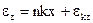(3.4)

где 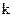- общий коэффициент усиления в управляющем контуре гирокомпаса; n – некоторый масштабный коэффициент; 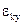, 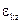- дополнительные углы кручения торсионов, вызываемые сигналами коррекции от вычислительного устройства.

Коэффициент усиления 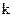зависит от характеристик электромеханических элементов управляющего контура. Преимущество гирокомпаса с косвенным управлением состоит в возможности дистанционно изменять величину этого коэффициента, тем самым регулируя передаваемые гироскопу управляющие моменты.

Итак, совокупная система дифференциальных уравнений для гирокомпаса с КУ может быть записана в форме:

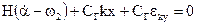
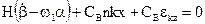(3.5)

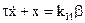
При работе на неподвижном основании сигналы коррекции гирокомпаса формируются в вычислительном устройстве таким образом, что

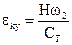и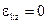

Следовательно, система (3.5) в этом случае упрощается и может быть представлена в форме:

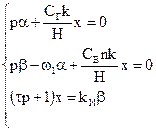(3.6)

где .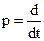

Найдем положение динамического равновесия гирокомпаса. Полагая 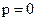, получим:

;

;

,

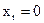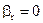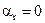т.е. гирокомпас на неподвижном основании не имеет девиации (с точностью до ошибок сигналов коррекции).

Относительно нулевого положения динамического равновесия чувствительный элемент гирокомпаса совершает колебания.

Для исследования этих колебаний из системы (3.6) составим характеристический определитель:

,

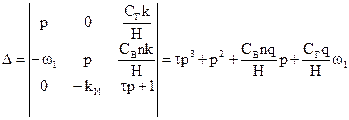где .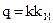

Поскольку правая часть системы (3.6) равна нулю, азимутальные колебания чувствительного элемента (ЧЭ) происходят в соответствии с уравнением

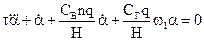(3.7)

Такой же вид имеет и уравнение колебаний ЧЭ по высоте.

Соответствующее уравнение третьего порядка

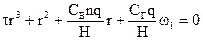
при определенных соотношениях между коэффициентами имеет один отрицательный вещественный корень и два комплексно-сопряженных с отрицательной вещественной частью:

; .

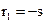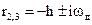Следовательно, решение уравнение (3.7) имеет вид:

,

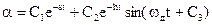где 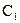, 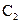и 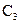- постоянные интегрирования.

Таким образом, движение гирокомпаса по азимуту состоит из суммы апериодического движения и затухающих колебаний с частотой .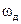

При очень малой постоянной времени индикатора горизонта 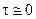мы получили бы характеристическое уравнение второго порядка. В этом случае азимутальное движение гирокомпаса на неподвижном основании было бы просто затухающим колебательным.

Однако постоянная времени 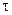должна быть достаточно большой (см. ниже). При некоторых значениях 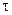движение гирокомпаса может стать неустойчивым.

Найдём условия, при которых сохраняется устойчивое движение гирокомпаса. Для этого воспользуемся критерием Гурвица. В соответствии с критерием Гурвица движение, характеризуемое дифференциальным уравнением третьего порядка, будет устойчивым, если:

все коэффициенты в характеристическом уравнении положительные;

выполняется неравенство

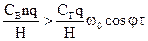
или

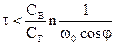. (3.8)

Обеспечение положительных значений всех коэффициентов характеристического уравнения достигается правильным включением всех электроэлементов гирокомпаса.

Неравенство (3.8) показывает, что при 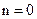(т. е. при отключении датчика вертикального момента) движение гирокомпаса будет неустойчивым для любых конечных значений т. В этом состоит отличие рассматриваемого компаса от обычного одногироскопного, у которого отключение демпфирующего устройства еще не означает потери устойчивости движения.