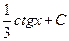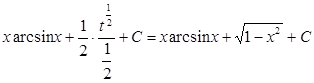Интегрирование по частям
Пусть u=u(x) и v=v(x) – две дифференцируемые функции. Найдём дифференциал от произведения этих функций.
duv= udv + vdu
Отсюда, интегрируя, получаем
∫ duv = ∫ udv + ∫ vdu
uv = ∫ udv + ∫ vdu
Формула интегрирования по частям:
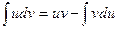 (9)
(9)
С помощью формулы интегрирования по частям вычисление интеграла ∫udv сводится к вычислению интеграла ∫vdu, если последний окажется проще исходного.
Полезно запомнить следующие типы интегралов, вычислять которые удобно интегрированием по частям:
а) 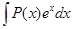 ;
; 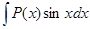 ;
; 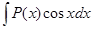
u=P(x)
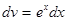 ;
; 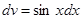 ;
; 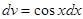
б) 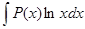 ;
; 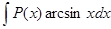 ;
; 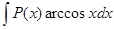
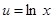 ;
; 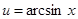 ;
; 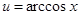
dv=P(x)dx
в) 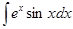 ;
; 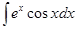
u=ex
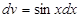 ;
; 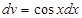

 Примеры:Используя формулу интегрирования по частям (9), найти интегралы:
Примеры:Используя формулу интегрирования по частям (9), найти интегралы:
| |||
| |||
1. 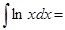
= 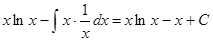
| |||||
 | 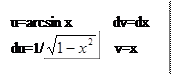 | ||||
2. 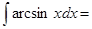
|
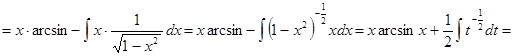
 |
6. Варианты для самостоятельной работы
Вариант 1 Найдите следующие интегралы  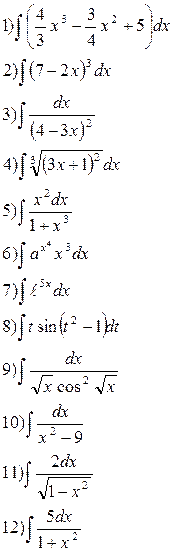 | Вариант 2 Найдите следующие интегралы  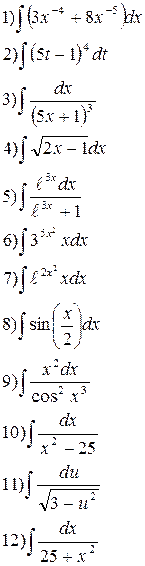 |
Вариант 3 Найдите следующие интегралы 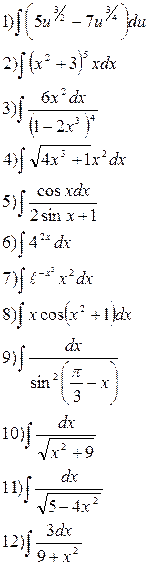 | Вариант 4 Найдите следующие интегралы 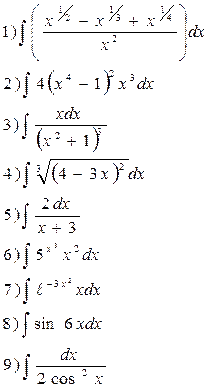 10) 10) 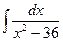 11) 11) 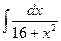 12) 12) 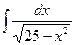 |
Вариант 5 Найдите следующие интегралы 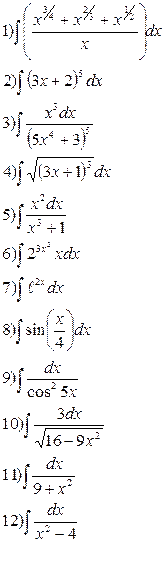 | Вариант 6 Найдите следующие интегралы 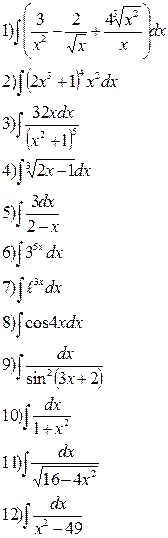 |
7. Образец решения варианта 1
| 1. | 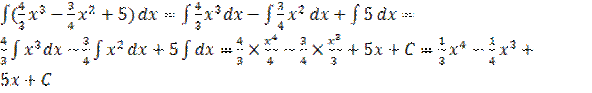 |
| 2. | 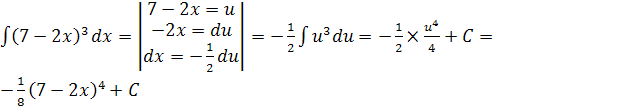 |
| 3. | 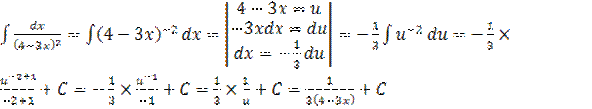 |
| 4. | 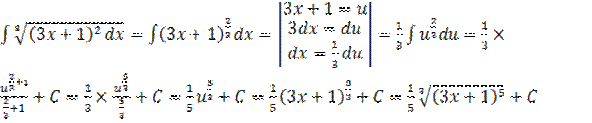 |
| 5. | 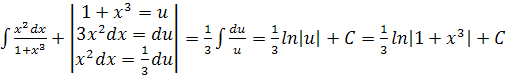 |
| 6. | 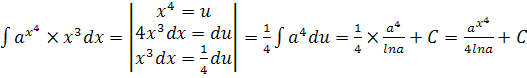 |
| 7. | 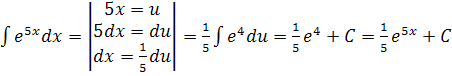 |
| 8. | 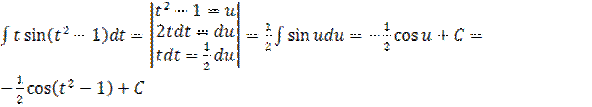 |
| 9. | 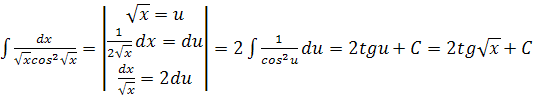 |
| 10. | 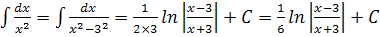 |
| 11. | 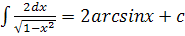 формула формула 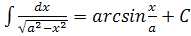 |
| 12. | 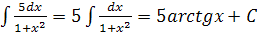 формула формула 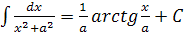 |
8. Тесты
1. Неопределенный интеграл 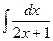 равен
равен
А. 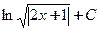
Б. 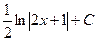
В. 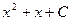
Г. 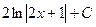
2. Первообразная для функции
y = x3 – 2 имеет вид
А. 3x2 + C
Б. 3x4 – 2 x + C
В. 6x4 - 2 + C
Г. x4/4 - 2x + C
3. 3 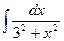 равен
равен
А. 3 arctgx + C
Г. 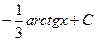
В. 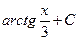
Г. -3 arctgx + C
4. ò7х dx равен
А. 7xln7 + C
Б. 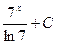
В. x×7x-1 + C
Г. 7x-1 + x + C
5. Первообразная для функции y = 2x + ex имеет вид
А. хеx + С
Б. х2еx-1 + С
В. x2 + еx +С
Г. 2xex+1 + C
6. ò5sinx dx равен
А. -5сosx + C
Б. 5cosx + C
В. cos5x + C
Г. – cos5x + C
7. 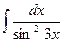 равен
равен
А. ctg3x + C
Б. 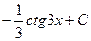
В. 3ctg3x + C
Г.