Общие сведения о плоских фермах. Простые фермы
Плоские фермы
Фермы являются шарнирно - стержневыми системами, в которых элементами являются стержни, шарнирно скрепленные между собой по концам.
Точки соединения стержней (в любой стержневой системе) называются узлами.
Для подсчета числа степеней свободы шарнирно - стержневой системы можно элементами считать узлы, а стержни, соединяющие узлы, – связями. При этом каждый узел считается обладающим двумя степенями свободы в плоскости и тремя в пространстве.
В обычных фермах стержни соединены между собой не шарнирно, а жестко, однако и в этом случае к ним применяется шарнирно - стержневая расчетная схема.
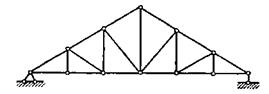
В фермах, применяемых для перекрытий и покрытий, а также для мостов, различают верхний и нижний пояса и решетку. Решетка состоит из наклонных раскосов и вертикальных стоек. Раскосы, понижающиеся к середине пролета, называются нисходящими, а повышающиеся – восходящими. Ферма по длине пролета делится на панели, обычно ограниченные соседними узлами поясов. В однопролетной ферме, нагруженной действующей вниз нагрузкой, верхний пояс сжат, а нижний – растянут, нисходящие раскосы вблизи опор ферм растянуты, а восходящие – сжаты. Стойки решетки при нагрузки по верхнему поясу сжаты, а при нагрузке по нижнему поясу – растянуты. В консольных фермах верхний пояс растянут, а нижний – сжат.

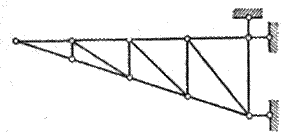
Зависимость между числом узлов и числом стержней в простой ферме.
Кинематический анализ ферм
Для кинематического анализа ферм можно использовать общую формулу, однако удобнее применять специальную формулу для ферм.
Пусть: У – число узлов фермы;
С – число стержней, включая опорные.
Каждый узел можно рассматривать как точку, которая имеет две степени свободы на плоскости XY, а каждый стержень уничтожает число степеней свободы на единицу, таким образом:
W = 2У – С – для плоской фермы;
W = 3У – С – для пространственной фермы.
Примечание: при применении этой формулы шарнирно неподвижную опору следует рассматривать как два стержня.
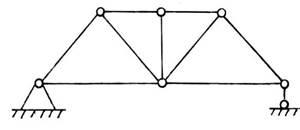
Пример № 1
У = 6; С = 9 + 3 = 12;
W = 2 * 6 – 12 = 0 – ферма геометрически неизменяема.
. 
Пример № 2
У = 4; С = 5 + 4 = 9;
W = 2 × 4 – 9 = -1 – ферма геометрически неизменяема с лишними связями.
Число лишних связей: Л = -W = 1.
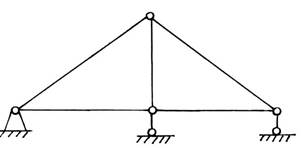
Статически определимые и статически неопределимые фермы
Условие статической определимости фермы
Связь фермы с землей (или каким-либо другим основанием) схематически изображается тремя стержнями, не пересекающимися в одной точке, геометрически неизменяема. Такая связи статически определима, так как число усилий в этих стержнях равно числу уравнений статики ( 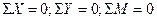 ), которые можно составить для плоской системы сил, находящейся в равновесии.
), которые можно составить для плоской системы сил, находящейся в равновесии.
Ферма статически определима относительно опорных закреплений лишь в том случае, когда число параметров, определяющих реакции этих закреплений, равно трем.
Этому условию удовлетворяют, например, следующие две системы опорных закреплений:
- комбинация шарнирно-подвижной и шарнирно-неподвижной опор – для ферм, опирающихся в двух точках:
- комбинация трех шарнирно-подвижных опор – при наличии трех опорных точек в сооружении; при этом направления реакций всех трех опор не должны пересекаться в одной точке и не должны быть параллельны друг другу.
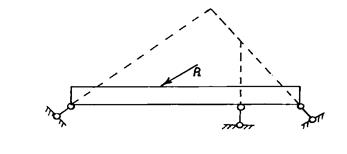
Наличие у геометрически неизменяемой фермы четырех опорных стержней и более, среди которых имеется три стержня с направлениями осей, не пересекающимися в одной точке и непараллельными друг другу, указывает на то, что ферма статически неопределима.
Статически неопределимое сооружение нельзя рассчитать при помощи одних лишь уравнений статики; для этого требуется составить дополнительные уравнения, основанные на изучении его деформаций.
Всякая простейшая ферма является системой геометрически неизменяемой и одновременно статически определимой.
Ферма будет статически определима, если число стержней ее С равно удвоенному числу узлов У минус 3: С = 2У –3.
Если при подсчете стержней фермы учесть и опорные стержни, то условие примет вид: 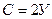 . Если геометрически неизменяемая ферма (система) в своем составе имеет число стержней, превышающее минимальное необходимое, то она является статически неопределимой.
. Если геометрически неизменяемая ферма (система) в своем составе имеет число стержней, превышающее минимальное необходимое, то она является статически неопределимой.
