Характеристики направляющего устройства

Кинематическая схема направляющего устройства определяет взаимосвязь между характеристиками упругого и демпфирующего устройств подвески и соответствующими характеристиками её упругого элемента и амортизатора, т.е. между вертикальными силами, действующими на колесо, и его вертикальными перемещениями и силами, действующими на упругий элемент и амортизатор, и их соответствующей деформацией (перемещением). В зависимых рессорных подвесках эти характеристики совпадают. В рычажных независимых подвесках эти характеристики, как правило, различаются.

Общие представления о закономерностях связи между силовыми факторами при оценке этой взаимозависимости можно получить на примерах, показанных на рис 2.2. Например, на схеме рис. 2.2-а упругий элемент (пружина) испытывает деформацию трех видов: осевую 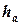от действия силы 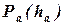; изгиба 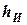в направлении поперечной силы 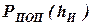; изгиба от момента 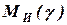в результате поворота рычага на угол 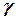. Согласно принципу возможных перемещений, пренебрегая трением в подвеске, можно записать:

.

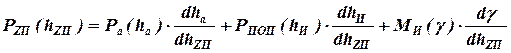При шарнирном креплении упругого элемента к рычагу и несущей системе автомобиля (рис. 2..2-б) последнее выражение упрощается, т.к. сила 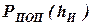и момент 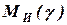равны нулю. Для этого случая зависимость силовых факторов подвески и упругого элемента будет иметь вид:

,

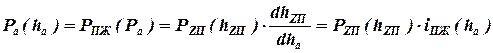где 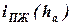-- передаточное число направляющего устройства для упругого элемента: .

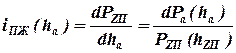Дифференцируя последнее выражение по 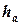, и выполнив преобразования, получим формулу для коэффициента жесткости упругого элемента подвески:

.

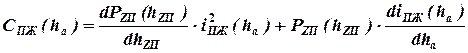Если принять упругую характеристику упругого устройства 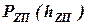линейной, что возможно при малых деформациях подвески относительно статического положения, то получим:

.

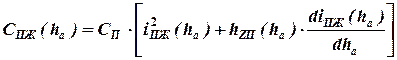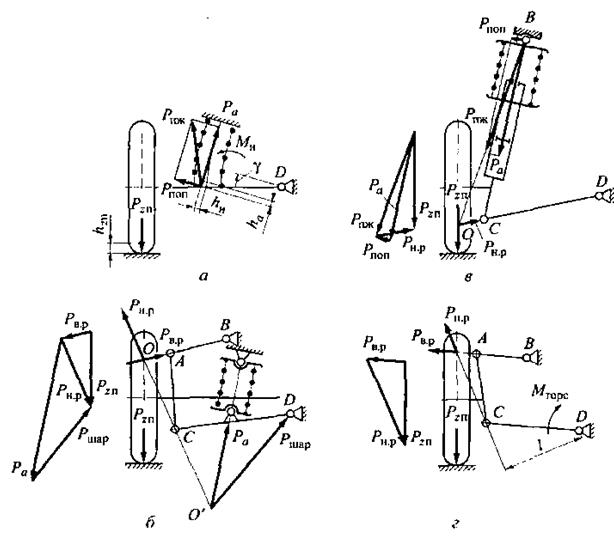
Рис. 2.2. Расчетные схемы независимых подвесок:

а – однорычажной с жестко закрепленной пружиной; б – двухрычажной с шарнирно закрепленной пружиной; в – рычажно-телескопической; г – двухрычажной с нижним расположением торсиона

Три последние выражения позволяют рассчитать нагрузочную характеристику и коэффициент жесткости упругого элемента, при заданных нагрузочной характеристике упругого устройства и кинематической схеме направляющего устройства подвески.

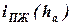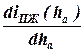При получении аналитических зависимостей и для некоторых конструктивных вариантов независимой подвески возникают определенные трудности. Поэтому в таких случаях целесообразно использовать графоаналитический метод расчета величин, в основу которого положено отношение: 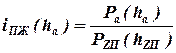. Величину 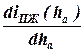при этом определяют графическим дифференцированием зависимости 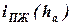, построенной по значениям отношения 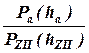для нескольких положений колеса. При подстановке значения производной в выражения для коэффициента жесткости упругого элемента подвески следует учитывать её знак.

Силу 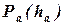задают произвольно, т.к. оценивают отношение сил, а 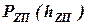находят из силового треугольника (см. рис. 2.2-б и -в). Прогиб упругого устройства 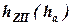для соответствующих значений 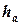определяют по чертежу кинематической схемы направляющего устройства.

Для вычисления коэффициента жесткости упругого элемента торсионной подвески (рис.2.2-г) можно использовать последнее выражение для этого коэффициента ( 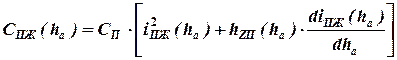), если заменить 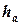на 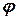, а величины 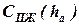и 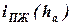принять равными:

; ,

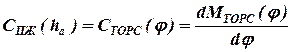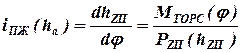где 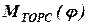-- момент, скручивающий торсион; 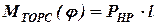, где 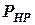-- сила, действующая на нижний рычаг; 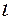-- плечо силы 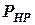; 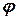-- угол закрутки торсиона. Значения силы 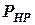и плеча 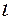находят графическим способом.

При переходе от нагрузочной характеристики демпфирующего устройства к нагрузочной характеристике амортизатора, и при решении обратной задачи, необходимо также учитывать кинематическую схему направляющего устройства подвески. Для схемы подвески на рис. 2.2-в, в которой отсутствует упругий элемент, можно записать следующее равенство:

,

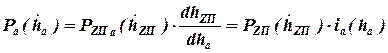где 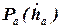и 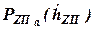-- действительная и приведенная к центру пятна контакта шины с опорной поверхностью силы сопротивления амортизатора;

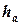-- деформация подвески вдоль оси амортизатора;

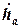и 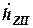-- скорость деформации подвески вдоль оси амортизатора и упругого устройства соответственно;

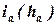-- передаточное отношение направляющего устройства по деформации: .

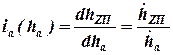Дифференцируя последнее равенство по скорости деформации 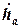, получим выражение для определения коэффициента сопротивления амортизатора:

.

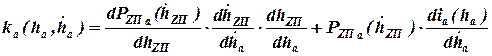Как и для коэффициента жесткости упругого элемента, при линейной зависимости 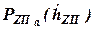последнее выражение упрощается и принимает вид:

,

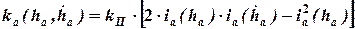где 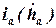-- передаточное отношение направляющего устройства по скорости деформации: .

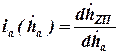Во всех рассмотренных выше выражениях, определяющих взаимосвязи между приведенными к центру пятна контакта шины с опорной поверхностью и реальными характеристиками упругого и демпфирующего элементов подвески, использовались только оценочные показатели – силы, деформации и скорость деформации. Поэтому такой подход к расчету характеристик направляющего устройства целесообразно применять на заключительном этапе проектирования подвески – при их проверке. В этом случае в расчетные формулы в явном виде входят геометрические параметры направляющего устройства подвески и установочные параметры колеса. Исходными характеристиками направляющего устройства в этом случае являются передаточные отношения, связывающие прогибы и силы:

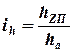и .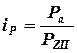

В этом случае при определении нагрузочной характеристики упругого элемента следует использовать 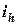и 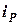, т.е. одновременно изменить масштаб по осям абсцисс и ординат на графике нагрузочной характеристики упругого устройства подвески, а коэффициент жесткости упругого элемента рассчитать по формуле:

.

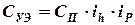Для некоторых схем направляющего устройства .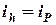

Нагрузочную характеристику амортизатора обычно получают, используя только передаточное отношение 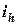. В этом случае коэффициент сопротивления амортизатора:

.

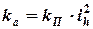Передаточные отношения 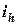и 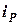очень редко остаются постоянными во всем диапазоне значений прогибов подвески. Поэтому при расчете следует учитывать значения передаточных отношений, соответствующие статической нагрузке.

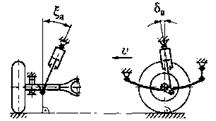
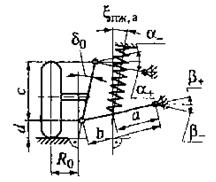
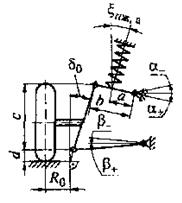
На рис. 2.3, в качестве примера, приведены расчетные схемы и расчетные зависимости для вычисления передаточных отношени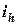й и 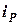направляющего устройства подвески, полученные на основе анализа соотношений геометрических параметров элементов этого устройства в известных конструкциях подвесок и силовых факторов.

Кинематическая схема направляющего устройства подвески оказывает существенное влияние на поперечно-угловые колебания (перемещения) подрессоренной массы автомобиля, приходящейся на соответствующую подвеску. Это влияние будет рассмотрено при определении исходных данных для расчета стабилизатора поперечной устойчивости.

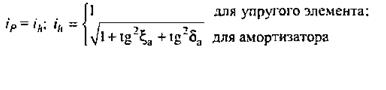
а.

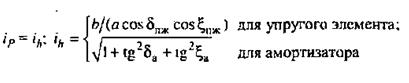
б.

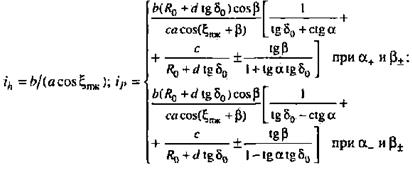
в.

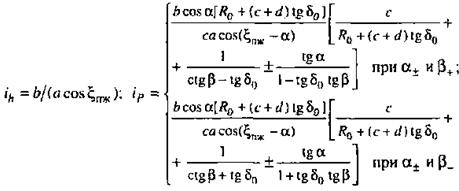
г.

Рис. 2.3. Расчетные зависимости для вычисления передаточных отношени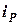й и 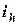направляющего устройства подвесок:

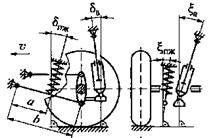
а–зависимая рессорная; б–зависимая пружинная с четырьмя продольными штангами; в–независимая с двумя поперечными рычагами разной длины и пружиной на нижнем рычаге; г–независимая с двумя поперечными рычагами разной длины и пружиной на верхнем рычаге

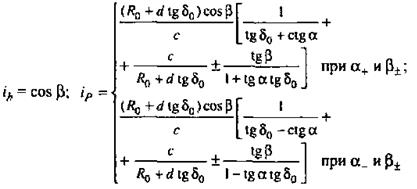
д.

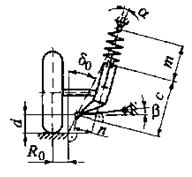
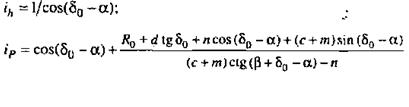е.

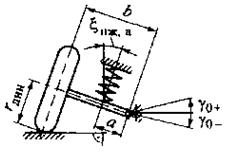
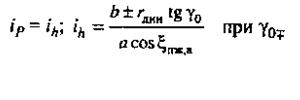
ж.

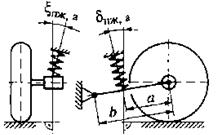
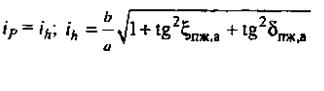
з.

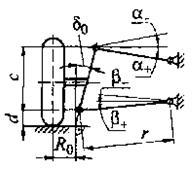
Рис. 2.3. (продолжение) Расчетные зависимости для вычисления передаточных отношени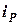й и 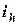направляющего устройства подвесок:

д–независимая с двумя поперечными рычагами разной длины и торсионом на нижнем рычаге; е–независимая рычажно-телескопическая; ж-независимая однорычажная с качанием рычага в поперечной плоскости; з–независимая однорычажная с качанием рычага в продольной плоскости

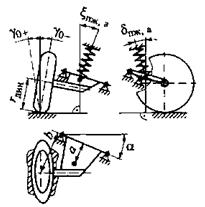
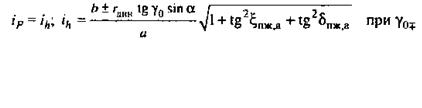
и.

Рис. 2.3. (окончание) Расчетные зависимости для вычисления передаточных отношени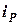й и 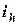направляющего устройства подвесок: и – независимая диагонально-рычажная