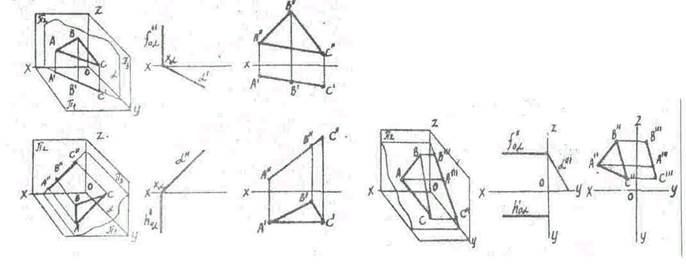
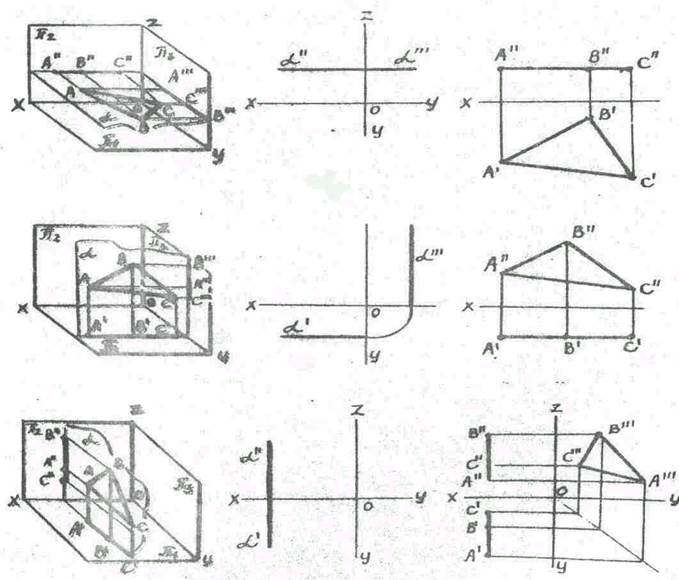
Взаимное положение точки и прямой, двух прямых. Определение видимости проекций точек на скрещивающихся прямых

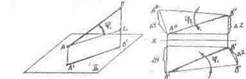Точка и прямая в пространстве занимают разное положение относительно друг друга.

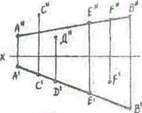
С (С', С") — находится над прямой АВ. D (D', D") — находится под прямой АВ. Е (Е', Е") — принадлежит прямой АВ.

F (F', F") — находится за прямой АВ.

Две прямые в пространстве могут быть параллельными, пересекающимися и

скрещивающимися.

Если прямые параллельные, то их соответствующие проекции то же

параллельные (A'BV/, C'D', A"B"//C"D").

Если две прямые пересекаются, то они имеют общую точку. Проекции этой

точки дожны лежать на одной липни связи.

Если две прямые не параллельные и не пересекаются, то они

скрещивающиеся. Проекции этих прямых на чертеже могут пересекаться, но точки пересечения их про­екций не лежат на одной линии связи.

Видимость проекций прямых, которые скрещиваются, определяется по правилу конкурирующих точек — точек, принадлежащих скрещивающимся прямым и расположенных на одной и той же проецирующей прямой. Видимость фронтальных проекций определяется видимостью конкурирующих точек 1 и 2. В этом случае видимой, ближайшей к наблюдателю, является проекция C'D'. Видимость горизонтальных проекций прямых определяется видимостью

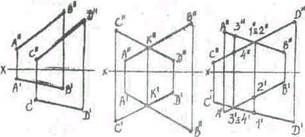конкурирующих точек 3 и 4. видимой проекцией здесь является А'В'.

7. Способы задания плоскостей. Плоскости частного и общего положения на эпюре Монжа.Плоскостью называется множество точек равноудалённых от двух точек пространства. Плоскость задается следующим образом:

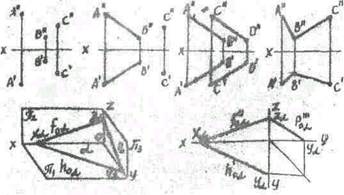^проекциями трех точек, не лежащих на одной прямой; 2) проекцией прямой и точки, не лежащей на прямой; 3) проекцией плоской фи­гуры; 4) проекциями двух прямых, которые пересекаются; 5) проекциями двух параллельных прямых; 6) следами плоскости (линия пересечения заданной плоскости с плоскостью проекций называется следом). Плоскости относительно плоскостей проекций

могут занимать общее и частное положения. Плоскости, не перпендикулярные ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскости частного положения делятся на про­ецирующие плоскости, перпендикулярные к одной из плоскостей проекций, и на плоскости, параллель­ные одной из плоскостей проекций. Проецирующие плоскости делятся на: 1) горизонтально-проецирующие, перпендикулярные к плоскости проекций П ; фронтально-проецирующие, перпендику­лярные к плоскости проекций П ; профильно-проецирующие, перпендикулярные к плоскости проекций П-. Проецирующие прямые обладают собирательным свойством, а именно: все геометрические образы,

принадлежащие плоскости, проецируются в линию на ту плоскость, перпендикулярно которой она раз­мещена. Плоскости, параллельные плоскостям проекций, делятся на: горизонтальные, фронтальные, профильные.