Для замкнутого контура.

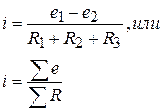
Билет №4. Метод эквивалентных преобразований.
Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.
Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином "эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи.
Схематичный пример использования метода эквивалентного преобразования схемы для расчета сложной электрической цепи изображен ниже:
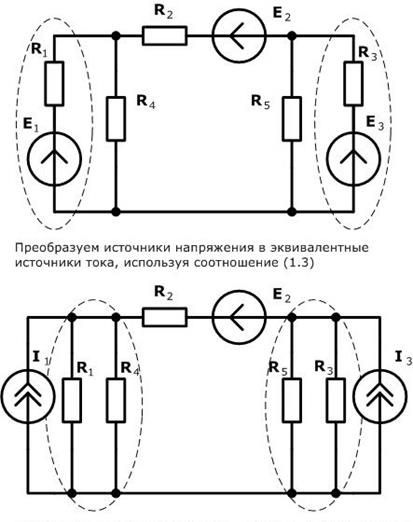
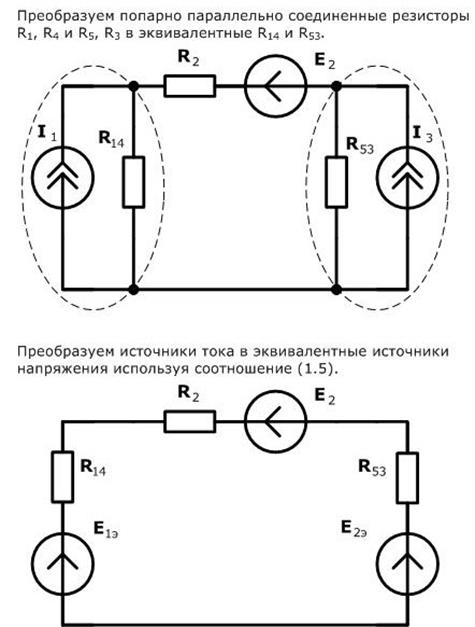
Полученная эквивалентная одноконтурная схема содержит только одну непреобрзованную ветвь: R2 и E2. Расчет тока в этой ветви не представляет сложностей, после чего становится очевидным расчет остальной части исходной схемы.
Пример:
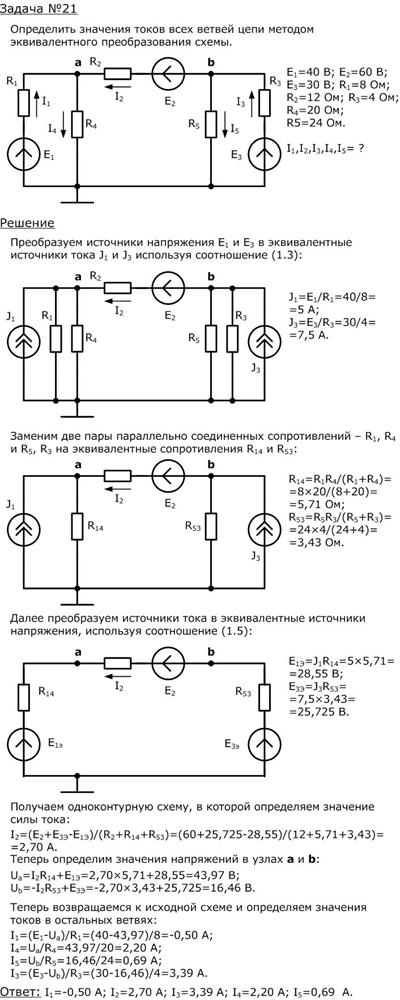
Билет №5. Метод токов ветвей. Число независимых уравнений. Порядок расчета. Пример.
Расчет разветвленных цепей с несколькими источниками выполняется методом уравнений Кирхгофа
Рис. 2.6.
Схема рис. 2.6 имеет 4 узла 6 ветвей, 1 источник тока.
N1 = NУ –1 = 3
N2 = N6 – NУ + 1 – NИ.Т = 2
Следовательно, для определения 5 неизвестных токов необходимо составить 3 уравнения по первому закону Кирхгофа и 2 уравнения по второму закону Кирхгофа.
1 закон Кирхгофа:
2 Закон Кирхгофа:
Для определения 5 неизвестных токов необходимо решить систему уравнений, составленных по первому и второму законам Кирхгофа.
Билет №6. Метод контурных токов
Метод контурных токов (МКТ) является одним из основных методов расчета ЭЦ, которым широко пользуются на практике. При расчете цепи этим методом полагают, что в каждом независимом контуре протекает свой контурный ток, направление которого выбирается произвольно. Уравнения составляют относительно контурных токов. После их нахождения их определяют токи ветвей через контурные токи.
Для цепи, содержащей NН.К = NB – NУ +1 – NИ.Т. независимых контуров, каноническая система контурных уравнений имеет вид:
R11IK1 + R12IK2 + … + R1NIKN = E11;
R21IK1 + R22IK2 + … + R2NIKN = E22;
………………………………………………… (2.3)
RN1IK1 + RN2IK2 + … +RNNIKN = ENN,
где R11, R22, … , RNN - собственные сопротивления 1 – го, 2 – го, …,
N–го контура (сумма сопротивлений всех ветвей, входящих в контур);
RKN, RLM = RML – взаимные (общие) сопротивления L – го и M – го контуров;
E11, E22, …, ENN - алгебраическая сумма ЭДС, входящих в 1 – ий,
2 – ой, … N – ый контур.
Правила составления уравнений по МКТ
Уравнения составляются для независимых контуров. Направление обхода контуров совпадают с выбранными произвольно направлениями контурных токов.
Если контурные токи, протекающие через общее сопротивление для двух контуров, направлены встречно то падение напряжения на нем записывается со знаком «-», если согласно – со знаком «+».
Если направление ЭДС в контуре совпадает с направлением контурного тока, то эта ЭДС записывается в уравнение со знаком «+», если не совпадает – со знаком «-».
Ток в любой ветви определяется как алгебраическая сумма контурных токов, протекающих по этой ветви. Со знаком «+» берется контурный ток, совпадающий по направлению с током ветви и со знаком «-» - направленный противоположно.
Если цепь содержит Nт источников тока, то кроме независимых контуров, необходимо выбрать контура, в которые входили бы источники тока. Контурные токи в них будут известны и равны токам источникам тока.
Порядок расчета по МКТ
1. Определяется число уравнений;
2. Выбираются независимые контуры;
3. Произвольно выбираются направления токов ветвей и контурных токов;
4. Составляется и решается система контурных уравнений;
5. Определяются токи ветвей.
Пример:Для цепи рис. 2.7 определить токи ветвей с помощью МКТ.
Рис. 2.7.
Решение:
NB = 6; NУ = 4; NT = 1;
 NН.К. = 6 – 4 + 1 – 1 = 2;
NН.К. = 6 – 4 + 1 – 1 = 2;
IK1(R1 + R2 + R3) + IK2R3 + IK3R2 = E1 – E3
IK1R3 + IK2(R3 + R4) – IK3R4 = E2 – E3
IK3 = J
Токи ветвей равны:
I1 = IK1; I2 = IK2; I3 = - IK1 – IK2;
I4 = IK2 – J; I5 = – IK1 – J.
Билет №7. Метод узловых напряжений
Методом узловых напряжений (МУН) можно определить значения токов и напряжений в электрической цепи, если найти потенциалы узлов, отсчитанные относительно некоторого одного узла, называемого базисным или опорным. Потенциал базисного узла принимается равным нулю. Напряжения в узлах цепи, отсчитанные относительно опорного, называются узловыми напряжениями.
 Для цепи, имеющей
Для цепи, имеющей 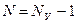 независимых узлов, каноническая система узловых уравнений имеет вид:
независимых узлов, каноническая система узловых уравнений имеет вид:
G
11U
1 – G
12U
2 – … – G
1NU
N = SEG + SJ
– G
11U
1 + G
22U
2 – … – G
2NU
N = SEG + SJ
………………………………………………… (2.4)
– G
N1U
1 – G
N2U
2 – … – G
NNU
N = SEG + SJ
где G11, G22 … GNN – собственные проводимости 1 – го, 2 – го …
N – го узлов, равные сумме проводимостей ветвей, сходящихся в 1 – м,
2 – м … N – м узле;
GKM = GMK – взаимные (общие) проводимости между узлами К и М, равные сумме проводимостей ветвей, содержащие эти узлы;
SEG, SEG … SEG – алгебраическая сумма произведений ЭДС ветвей,
примыкающих к 1 – му, 2 – му … N – му узлу, на их проводимости;
SJ, SJ …SJ – алгебраическия сумма токов источников тока,
присоединенных к соответствующему узлу.

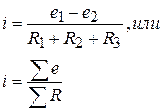




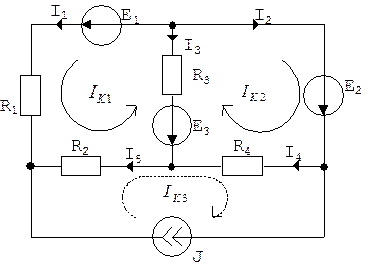
 NН.К. = 6 – 4 + 1 – 1 = 2;
NН.К. = 6 – 4 + 1 – 1 = 2; Для цепи, имеющей
Для цепи, имеющей 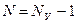 независимых узлов, каноническая система узловых уравнений имеет вид:
независимых узлов, каноническая система узловых уравнений имеет вид: