Множественная линейная регрессия в скалярной и векторной формах

Обобщением модели парной регрессии является модель множественной регрессии. Множественная регрессия – уравнение связи с несколькими независимыми переменными:

,

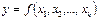где 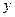– зависимая переменная (результативный признак);

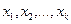– независимые переменные (факторы).

Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Чаще всего используются линейные уравнения множественной регрессии:

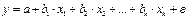. (2.1)

Построение модели связано с выбором вида уравнения и отбором факторов модели. Факторы, включаемые в модель, должны удовлетворять требованиям:

1. должны быть количественно измеримы;

2. не должны быть интеркоррелированы;

3. между факторами не должно быть высокой корреляционной связи, т.к. будет сложно определить влияние каждого фактора в отдельности на прибыль.

Для выявления мультиколлинеарных факторов можно использовать корреляционную матрицу :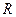

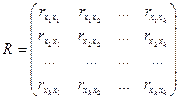
где 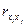– оценки коэффициентов парной корреляции. При этом, если факторы некоррелированы, то 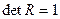, если между факторами линейная связь, то 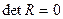и чем ближе 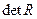к нулю, тем сильнее мультиколлинеарность. Один из путей устранения мультиколлинеарности – исключение из модели одного или нескольких коллинеарных факторов.

Для оценки параметров уравнения множественной регрессии используют МНК, для чего необходимо решить систему линейных уравнений

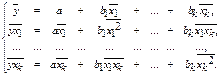
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:

,

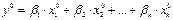где 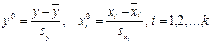– стандартизованные переменные;

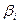– стандартизированные коэффициенты регрессии.

Связь коэффициентов множественной регрессии 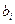со стандартизованными коэффициентами 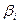описывается соотношениями:

.

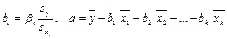Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле

.

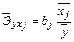Для расчета частных коэффициентов эластичности применяется формула

.

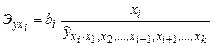На основе уравнения (2.1) могут быть найдены частные уравнения регрессии:

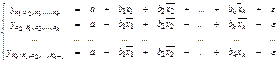
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

.

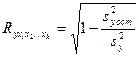Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

.

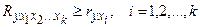Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде:

.

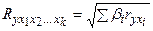Частные коэффициенты (или индексы) корреляции, измеряющие влияние на 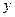фактора 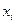при неизменном уровне других факторов, можно определить по формуле

.

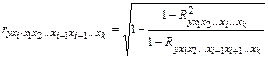Частные коэффициенты корреляции изменяются в пределах от –1 до 1.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции: .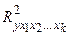

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле

,

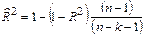где 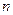– число наблюдений, 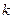– число факторов.

Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:

.

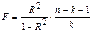Частный 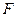-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора 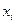частный 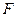-критерий определится как

.

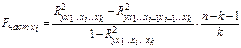Оценка значимости коэффициентов уравнения регрессии с помощью t-критерия Стьюдента сводится к вычислению значения

,

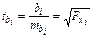где 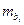– средняя квадратическая ошибка коэффициента регрессии 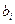и определяется по формуле

.

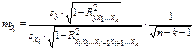Возможны случаи, когда в модель регрессии необходимо включить факторы, имеющие качественные признаки, например, образование, тип изделия, профессия и т.д.

Чтобы использовать эти переменные им придают численные значения. Такие искусственно сконструированные переменные в эконометрике называются фиктивными или структурными переменными.

Фиктивные переменные могут вводиться как в линейные, так и в нелинейные модели.