Первое начало термодинамики

Первое начало термодинамики выражает закон сохранения энергии для тех макроскопических явлений, где одним из ведущих параметров, определяющих состояние тел, является температура.

В механике доказывается, что для изолированной системы полная механическая энергия сохраняется. Но это справедливо не всегда, и только в тех случаях, когда все действующие силы консервативны. При наличии диссипативных сил - силы трения – механическая энергия уменьшается. Работа диссипативных сил превращается в тепло. Оказалось, что принцип сохранения энергии остаётся справедливым и при наличии диссипативных сил, если только расширить понятие энергии введением её новой формы – внутренней энергии, называемой тепловой энергией.

Нарушение механического закона сохранения энергии объясняется тем, что макроскопическое механическое движение не учитывает все виды движения. Из ее поля зрения ускользает внутреннее движение атомов и молекул, а также взаимодействия между ними.

Прежде чем сформулировать I начало термодинамики, введём некоторые важные величины термодинамики.

Макроскопическая работа

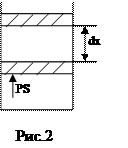Рассмотрим газ в цилиндре с поршнем. Пусть под этим поршнем находится сжатый газ (рис.2). Вычислим бесконечно малую или элементарную работу dA, совершаемую газом при бесконечно малом расширении, в котором его объём увеличивается на dV. Сила давления газа на поршень равна F=PS, где S – площадь поршня. Если поршень переместить на расстояние dx, то газ совершит работу δA=Fdx=PSdx. Учитывая, что Sdx=dV, имеем следующее выражение для элементарной работы

dA=PdV. (1.9)

В том случае, когда над газом совершается работа внешними силами, то

dA=-PdV.

Формула (1.9) верна не только для газов, но и для любых тел.

Если тело переходит из состояния 1 в состояние 2, то совершённая во время этого процесса работа определяется путём интегрирования уравнения (1.9)

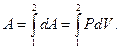(1.10)

Интеграл 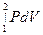можно определить графически. Это связано с тем, что состояние тела характеризуется точкой на кривой P=f(V). Поэтому, если зависимость P(V) построена графически, то 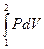равен площади под данной кривой.

Пусть система переходит из состояния M в состояние N вдоль кривой M1N (рис.3). Эта кривая определяет давление P, как вполне определённую функцию объёма V. После этого работа системы A определяется однозначно. Она численно равна площади криволинейной трапеции N₁M₁M1NN₁. Если систему заставить переходить из того же начального состояния M в то же конечное состояние N вдоль другой кривой M2N, то соответствующая работа A₁ изобразится площадью M₁M2NN₁. Как видно из рисунка A¹A₁. Это означает, что работа, совершаемая системой, при переходе из одного состояния в другое зависит от того, через какую последовательность состояний она проходит, т. е. зависит от формы пути перехода. Про такие величины говорят, что они не являются функциями состояния. Величины, которые не зависят от формы пути перехода, а зависят только от начального и конечного состояния системы являются функциями состояния.

Вычислим работу, совершаемую идеальным газом при различных изопроцессах. При изохорическом процессе dV=0, соответственно работа равна нулю. При изобарическом процессе P=const, тогда

.

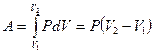При изотермическом процессе Т=const,

,

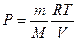работа будет равна

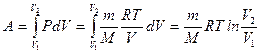. (1.11)