Теоремы об изменении кинетической энергии точки и системы

Работа силы. Мощность.

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.

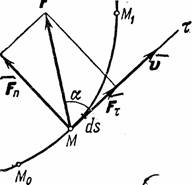
Рис.16

При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки.

Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds. Элементарной работой силы 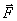(рис.16) называется скалярная величина:

,

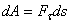где 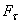- проекция силы 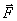на касательную к траектории, направленную в сторону перемещения точки, а 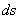-бесконечно малое перемещение точки, направленное вдоль этой касательной.

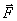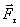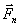Данное определение соответствует понятию о работе, как о ха­рактеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу на составляющие и , то изменять модуль скорости точки будет только составляющая 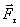, сообщающая точке касательное ускорение Составляющая же 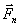или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном дви­жение изменяет давление на связь. На модуль скорости составляю­щая 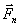влиять не будет, т.е., как говорят, сила 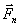«не будет про­изводить работу».

Замечая, что 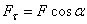, получаем:

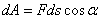. (1)

Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементар­ное перемещение 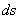или элементарная работа силы равна произведению модуля силы на элементарное перемещение 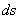и на косинус угла между направлением силы и направлением перемещения.

Если угол 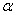острый, то работа положительна. В частности, при 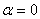элементарная работа .

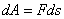Если угол 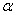тупой, то работа отрицательна. В частности, при 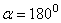элементарная работа .

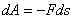Если угол 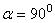, т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Найдем аналитическое выражение элементарной работы. Для этого разложим силу 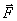на составляющие 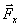, , 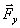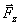по направлениям координатных осей (рис.17; сама сила 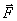на чертеже не показана).

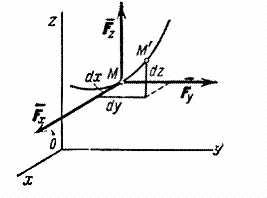
Рис.17

Элементарное перемещение 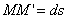слагается из перемещений 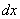, , 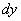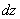вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы 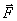на перемещении 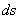можно вычислить как сумму работ её составляющих 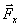, , 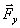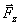на перемещениях , , .

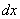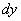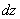Но на перемещении 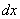совершает работу только составляющая 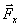, причем её работа равна 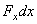. Работа на перемещениях 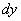и 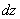вычисляется аналогично. Окончательно находим: .

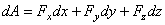Формула дает аналитическое выражение элементарной работы силы.

Работа силы на любом конечном перемещении М₀М₁ вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:

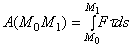
или

.

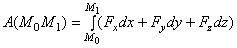Следовательно, работа силы на любом перемещении М₀М₁ равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям пере­менных интегрирования в точках М₀ и М₁.

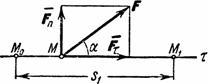
Рис.18

Если величина 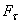постоянна ( 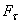= const), то и обозначая перемеще­ние М₀М₁ через 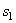получим: .

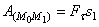Такой случай может иметь место, когда действующая сила постоянна по модулю и направлению (F= const), а точка, к ко­торой приложена сила, движется прямолинейно (рис.18}. В этом случае 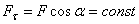и работа силы .

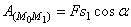Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).

Мощность

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

,

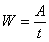где t - время, в течение которого произведена работа A. В общем случае

.

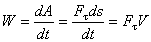Следовательно, мощность равна произведению касательной состав­ляющей силы на скорость движения.

Единицей измерения мощности в системе СИ является ватт (1 вт=1 дж/сек). В технике за единицу мощности часто принимается 1 лошадиная сила, равная 75 кГм/сек или 736 вт.

Работу, произведенную машиной, можно измерять произведением ее мощности на время работы. Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 квт-ч = 3,6 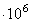дж 367100кГм).

Из равенства 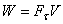видно, что у двигателя, имеющего дан­ную мощность W, сила тяги 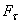будет тем больше, чем меньше ско­рость движения V. Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низшие передачи, позволяю­щие при полной мощности двигаться с меньшей скоростью и раз­вивать большую силу тяги.

Примеры вычисления работы

Рассмотренные ниже при­меры дают результаты, которыми можно непосредственно пользо­ваться при решении задач.

1) Работа силы тяжести. Пусть точка М, на которую действует сила тяжести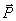 , перемещается из положения М_­0 (x­₀, у₀, z₀) в положение M₁ (х₁, у₁, z₁). Выберем оси координат так, чтобы ось Oz была направлена вертикально вверх (рис.19).

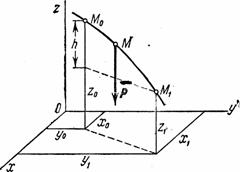
Рис.19

Тогда Р_x=0, Р_y=0, P_z= -Р. Подставляя эти значения и учитывая перемен­ную интегрирования z:

.

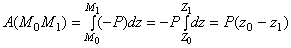Если точка M₀ выше М₁, то 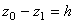, где h-величина вер­тикального перемещения точки;

Если же точка M₀ ниже точки M₁то .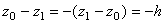

Окончательно получаем: .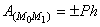

Следовательно, работа силы тяжести равна взятому со зна­ком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной. Из полученного результата следует, что работа силы тяжести не зависит от вида той траектории, по которой перемещается точка ее приложения.

Силы, обла­дающие таким свойством, назы­ваются потенциальными.

2) Работа силы упругости. Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к свободному концу некоторой пружины (рис.20,а). Отметим на плоскости точкой О поло­жение, занимаемое концом пружины, когда она не напряже­на ( 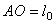- длина ненапряженной пружины), и примем эту точку за начало координат. Если теперь оттянуть груз от равновесного положения О, удлинив пружину до величины 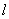, то на груз будет действовать сила упругости пружины F, направленная к точке О.

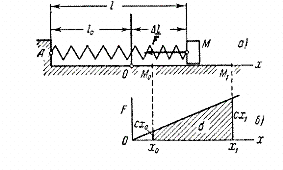
Рис.20

По закону Гука величина этой силы пропорциональна удлинению пружины 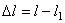. Так как в нашем случае 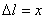, то по модулю .

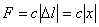Коэффициент сназывается коэффициентом жесткости пружины. В технике обычно измеряют величину с в H/см, полагая коэф­фициент с численно равным силе, которую надо приложить к пру­жине, чтобы растянуть ее на 1 см.

Найдем работу, совершаемую силой упругости при перемещении груза из положения 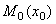в положение 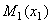. Так как в данном случае , , 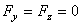то получим:

.

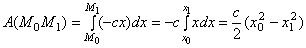(Этот же результат можно получить по графику зависимости F от х (рис.20, б), вычисляя площадь 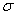заштрихованной на чертеже тра­пеции и учитывая знак работы.) В полученной формуле 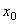представ­ляет собою начальное удлинение пружины 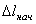, а 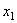конечное удлинение пружины 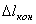. Следовательно,

,

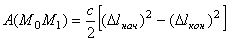т.е. работа силы упругости равна половине произведения коэффи­циента жесткости на разность квадратов начального и конеч­ного удлинений (или сжатий) пружины.

Работа будет положительной, когда 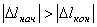, т. е. когда конец пружины перемещается к равновесному положению, и отрица­тельной, когда 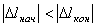, т.е. конец пружины удаляется от равновесия положения. Можно доказать, что формула ос­тается справедливой и в случае, когда пе­ремещение точки М не является прямо­линейным.

Таким образом, оказывается, что работа силы F зависит только от значе­ни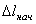й и 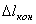и не зависит от вида траектории точки М. Следовательно, сила упругости также является потенциальной.

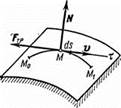
Рис.21

3) Работа силы трения. Рассмотрим точку, движущуюся по какой-нибудь шероховатой поверхности (рис. 21) или кривой. Действующая на точку сила трения равна по модулю fN, где f-коэффициент трения, а 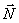-нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно, F_тр=-fN и по формуле

.

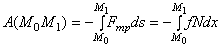Если величина силы трения постоянна, то 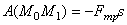, где s-длина дуги кривой М₀М₁ по которой перемещается точка.

Таким образом, работа силы трения при скольжении всегда отрицательна. Величина этой работы зависит от длины дуги М₀М₁ . Следовательно, сила трения является силой непотенциальной.

4) Работа силы, приложенной к телу, вращающемуся вокруг неподвижной оси.

В этом случае (рис.22) точка приложения силы 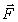движется по окружности радиуса r. Элементарная работа, по (1), 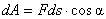, где .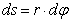

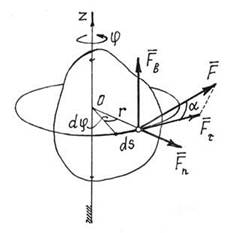
Рис.22

Поэтому .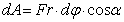

Но .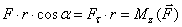

Это нетрудно установить, разложив силу на три составляющие (рис. 22). (Моменты сил 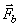и 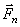равны нулю). Значит,

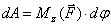(2)

В частности, если момент силы относительно оси 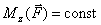, работа силы при повороте тела на угол 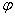равна

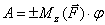. (3)

Знак работы определяется знаками момента силы и угла поворота. Если они одинаковы, работа положительная.

Из формулы (3) следует и правило определения работы пары сил. Если пара с моментом m расположена в плоскости перпендикулярной оси вращения тела, то ее работа при повороте тела на угол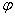

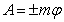. (4)

Если же пара сил действует в плоскости не перпендикулярной оси вращения, то ее надо заменить двумя парами. Одну расположить в плоскости перпендикулярной оси, другую – в плоскости параллельной оси. Моменты их определяются разложением вектора момента 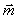по соответствующим направлениям: 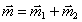. Конечно работу будет совершать только первая пара с моментом 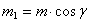, где 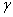– угол между вектором 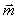и осью вращения z,

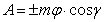. (5)