Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости

1. Дан куб ABCDA₁B₁C₁D₁. Точка М – середина B₁C₁, N – середина D₁С₁, К – середина DC, О – точка пересечения диагоналей квадрата ABCD. Определите угол между прямой и плоскостью и найдите его величину:

а) AB₁ и АВС; б) АС и АA₁В; в) MN и DD₁C;

г) MN и DD₁B; д) АМ и АВС; е) АС и MKN;

ё) АК и МКN; ж) АC₁ и ВСC₁; з) DC₁ и АСC₁;

и) В₁D и АСC₁; й) АА₁ и AMN; к) DD₁ и AMN.

2. MABCD – четырёхугольная пирамида, основание которой квадрат ABCD. МD перпендикулярно плоскости АВС, MD = AB, O – точка пересечения диагоналей квадрата ABCD. Определите угол между прямой и плоскостью и найдите его величину:

а) МС и АВС; б) МВ и АВС; в) МА и АВС;

г) МО и АВС; д) АС и МDС; е) АD и MDC;

ё) АВ и MDC; ж) АС и ОАМ; з) АО и ВСМ.

3. Стороны треугольника равны 51, 30 и 27. Из вершины меньшего угла треугольника проведён к его плоскости перпендикуляр длиной 10. Найдите расстояние от концов перпендикуляра до противоположной стороны треугольника.

4. Диагонали ромба равны 60 и 80. В точке пересечения диагоналей к плоскости ромба проведён перпендикуляр длиной 45. Найдите расстояние от конца перпендикуляра до стороны ромба.

Угол между плоскостями. Перпендикулярность плоскостей

1. Дан куб ABCDA₁B₁C₁D₁. Точка М – середина ребра D₁С₁. Укажите взаимное расположение плоскостей и найдите угол между ними:

а) A₁BА и D₁СD; б) A₁B₁C₁ и DD₁С; в) A₁BD и B₁D₁С;

г) B₁АС и ADC; д) A₁BD и C₁DВ; е) A₁BD и СC₁А;

ё) АB₁C₁ и ADC; ж) A₁МА и B₁C₁С; з) A₁МА и ВB₁D;

и) МA₁D и СA₁D.

2. В правильной пирамиде SABC высота SM равна 3, сторона основания АВ равна 18. Найдите угол между боковой гранью и основанием.

3. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ ребро АВ равно 2, ребро АA₁ равно 4. Найдите тангенс угла наклона диагонального сечения AB₁C₁D к основанию.

4. SABCD – правильная четырёхугольная пирамиды, в которой сторона основания равна 2, а угол между боковой гранью и основанием равен 45°. Найдите высоту пирамиды.

Раздел 5. МНОГОГРАННИКИ.

1. Найдите площадь полной поверхности прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, если

а) ABCD – квадрат со стороной 2, а AA₁ = 3;

б) AB = 6, AC = 10, AB₁ = 10;

в) ABCD – квадрат со стороной 4, а диагональ AC₁ = 6;

г) ABCD – квадрат со стороной 4, а диагональ AC₁ наклонена к основанию под углом 45⁰;

д) AB = 2, BC = 4, а плоскость AB₁C₁ наклонена к плоскости ABC под углом 60⁰.

2. Найдите объём прямоугольного параллелепипеда, если:

а) его измерения 2 см, 3 см и 4 см;

б) площадь его основания 3 см², а высота 5 см;

в) диагональ его основания равна 5 м, одна из сторон основания равна 4 м, а высота равна 2 м;

г) высота равна 3 см, диагональ его основания равна 2 см, а угол, образованные ею с одной из сторон основания, равен 30°.

3. Ширина комнаты 4 м, длина 5м, а высота потолка 3м. Общая площадь окон и двери 8 м². Найдите площадь обоев, которыми оклеены стены.

4. Прямоугольный параллелепипед с измерениями 1 м, 3 м и 5 м помещён внутрь куба с ребром 6 м. Сделайте рисунок для такого случая и найдите объём свободного места внутри куба.

5. Найдите объём куба, если его диагональ равна d.

6. Измерения прямоугольного параллелепипеда равны 6, 16 и 18. Найдите ребро равновеликого ему куба.

7. В основании прямого параллелепипеда лежит параллелограмм. Найдите его объём, если:

а) высота параллелепипеда 3 см, стороны основания 4 см и 5 см, а один из углов основания 135°;

б) высота параллелепипеда 5 см, диагонали основания 6 см и 10 см, а угол между диагоналями 30°.

8. Найдите объём правильной n-угольной призмы, у которой каждое ребро равно a, если: а) n = 3; б) n = 4; в) n = 6; г) n = 8.

9. Наибольшая диагональ правильной шестиугольной призмы равна 8 см и составляет с боковым ребром угол 30°. Найдите объём призмы.

10. В основании прямой призмы с высотой, равной 5, лежит трапеция. Найдите объём призмы, если:

а) трапеция прямоугольная с основаниями 4 и 2 и высотой 3;

б) трапеция равнобедренная с боковыми сторонами длины 10 и основаниями 18 и 6.

11. Найдите объём прямой призмы АВСА₁В₁С₁, если АВ=ВС=m, угол ABC равен φ и ВВ₁ = BD, где BD – высота треугольника АВС.

12. Найдите объём треугольной призмы АВСА₁В₁С₁, высота которой 3, если:

а) АВС – прямоугольный треугольник с катетами 2 и 4;

б) АВС – равносторонний треугольник со стороной 1.

13. Найдите объём треугольной призмы АВСА₁В₁С₁, если:

а) площадь основания АВС равна 5 см², а боковое ребро АА₁ равно 2 см и наклонено к плоскости основания под углом 30°;

б) АВС – равносторонний треугольник со стороной 3 см, а боковое ребро ВВ₁ равно 3 см и наклонено к плоскости основания под углом 45°.

в) АВС – треугольник со сторонами 5, 12 и 13, а высота А₁М грани АА₁В₁В наклонена к плоскости основания под углом 60° и равна 2.

г) АВС – треугольник со сторонами 6, 8 и 10, высота боковой грани АА₁В₁В равна 4, а угол между основанием и этой гранью равен 45°.

14. Основанием наклонного параллелепипеда является прямоугольник со сторонами a и b. Боковое ребро равно и составляет со смежными сторонами основания углы, равные φ. Найдите объём параллелепипеда.

15. Найдите объём пирамиды с высотой H, если:

а) H = 2 м, а основанием служит квадрат со стороной 3 м;

б) H= 2,2 м, а основанием служит треугольник АВС, в котором АВ = 20 см, ВС = 13,5 см, угол АВС равен 30°.

16. Найдите объём правильной четырёхугольной пирамиды, все рёбра которой 2.

17. Рассматривается четырёхугольная пирамида MABCD такая, что в основании её лежит квадрат со стороной 2, а её высота MA равна 3. Найдите площадь поверхности этой пирамиды.

18. Вычислите площадь боковой поверхности правильной треугольной пирамиды, если её высота равна 9, апофема – 18.

19. В правильной шестиугольной пирамиде апофема равна 15, высота – 12. Найдите площадь полной поверхности пирамиды.

20. Рассматривается правильная треугольная пирамида MABC, сторона основания которой равна 4, а угол наклона плоскости боковой грани MAB к плоскости основания равен 60°. Пусть MO – высота пирамиды, точка K – середина ребра AB. Найдите:

а) длину отрезка OK;

б) длину высоты MO;

в) площадь основания ABC;

г) объём пирамиды MABC.

21.Найдите объём треугольной пирамиды MABC, если:

а) все плоские углы с вершиной А прямые и AM = AB = AC = 1 см;

б) АВС – правильный треугольник со стороной 2 см, а ребро МА равно 3 см и наклонено к плоскости основания под углом 30°;

в) АВС – равнобедренный треугольник со сторонами АВ = ВС = 2 см и углом АВС = 120°, грань МАВ имеет площадь, равную 4 см², и перпендикулярна основанию АВС;

г) АВС – прямоугольный треугольник, гипотенуза АВ которого равна 13 см, а катет АС = 12 см, вершина М проектируется в середину гипотенузы АВ, грань МАС образует с основанием угол 45°;

д) она является правильной пирамидой, ребро основания которой равно 2 см, а боковое ребро наклонено к плоскости основания под углом 45°;

е) она является правильным тетраэдром, все рёбра которого равны 1.

д) угол наклона боковых граней к основанию.

22.Высота правильной треугольной пирамиды SABC равна 3 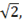а высота её основания равна 9. Найдите:

а) боковое ребро;

б) апофему;

в) сторону основания;

г) плоский угол при вершине S;

д) угол наклона боковой грани к основанию.

23.Сторона основания правильной шестиугольной пирамиды равна 2 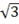, высота пирамиды равна 4. Найдите:

а) боковое ребро;

б) высоту основания пирамиды;

в) апофему;

г) расстояние от центра основания O до плоскости боковой грани;

д) расстояние от вершины A до плоскости BSC.

24. Найдите площадь боковой поверхности правильной треугольной пирамиды MABC, если:

а) MA = 5, AB = 6;

б) AB = 2, а высота пирамиды MO = 1;

в) AB = 2 и медиана боковой грани (апофемы) MK наклонена к плоскости основания под углом 30⁰;

г) высота MO равна 3, а плоскость боковой грани MAB наклонена к плоскости основания ABC под углом 45⁰.

25. Основанием пирамиды DABC является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29 см, катет АС равен 21 см. Ребро DA перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.

26. Основание пирамиды – квадрат со стороной 16 см, две боковые грани перпендикулярны плоскости основания. Вычислите площадь полной поверхности пирамиды, если её высота равна 12 см.

27. Основанием пирамиды является ромб со стороной 6 см. Каждый из двугранных углов при основании равен 45°. Найдите объём пирамиды, если её высота равна 1,5 см.

28. Основание пирамиды – ромб со стороной 15 см, каждая грань пирамиды наклонена к основанию под углом 45°. Найдите объём пирамиды, если площадь её боковой поверхности равна 300 см².

29. Основание пирамиды – прямоугольник, площадь которого равна 1 м². Две боковые грани перпендикулярны основанию, а две другие наклонены к нему под углами 30° и 60°. Найдите объём пирамиды.

30. Объём правильной пирамиды MABC равен 2 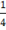см³. Основание АВС пирамиды – правильный треугольник со стороной 3 см. Найдите угол наклона к основанию бокового ребра МА.

31. Объясните, какой должна быть длина ребра правильного тетраэдра, чтобы его площадь полной поверхности была равна 4 см².

32. В правильной четырёхугольной усечённой пирамиде площади оснований равны 25 см² и 9 см², боковое ребро образует с плоскостью нижнего основания угол 45°. Вычислите площадь боковой поверхности пирамиды.

33. Найдите объём правильной четырёхугольной пирамиды, если:

а) её высота равна H, а двугранный угол при основании равен β;

б) сторона основания равна m, а плоский угол при вершине равен α.

34. Боковое ребро правильной четырёхугольной пирамиды равно m и составляет с плоскостью основания угол φ. Найдите объём пирамиды.

35. Сколько центров симметрии имеет:

а) параллелепипед;

б) правильная треугольная призма;

в) двугранный угол;

г) отрезок;

д) шар?

36. Сколько осей симметрии имеет:

а) отрезок;

б) правильный треугольник;

в) круг;

г) шар?

37. Сколько плоскостей симметрии имеет:

а) правильная четырёхугольная призма, отличная от куба;

б) правильная четырёхугольная пирамида;

в) правильная треугольная пирамида;

г) шар?

38. Сколько и каких элементов симметрии имеют правильные многогранники:

а) правильный тетраэдр;

б) правильный гексаэдр;

в) правильный октаэдр;

г) правильный икосаэдр;

д) правильный додекаэдр?