Решение систем линейных алгебраических уравнений матричным способом

Пусть даны матрицы

, ,

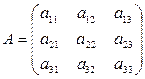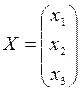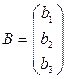
Тогда система линейных уравнений (5) может быть записана в матричном виде:

(7)

Допустим 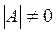, тогда для нее существует обратная матрица 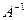. Умножим равенство (7) на 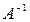слева: 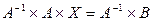, т.к. 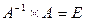, то имеем матричное решение системы линейных уравнений (5): .

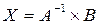g Решим матричным методом следующую систему:

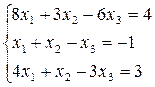
Матрицу, обратную к матрице, составленной из коэффициентов системы находим, см. п. 1.1.7.

g Самостоятельно решить матричным способом следующую систему:

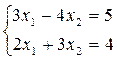
Решение систем линейных алгебраических уравнений методом исключения неизвестных (метод Гаусса).

· Под элементарными преобразованиями матриц понимаются следующие операции:

§ Перестановка строк (столбцов);

§ Умножение строки (столбца) на число, отличное от нуля;

§ Прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

· Матрицы, переходящие друг в друга в результате элементарных преобразований, называются эквивалентными: .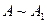

Для решения систем линейных алгебраических уравнений применяется также метод исключения неизвестных, называемый методом Гаусса. Основная идея этого метода состоит в том, что матрица системы, расширенная столбцом свободных членов, элементарными преобразованиями преобразуется к верхнетреугольному виду. Например,

,

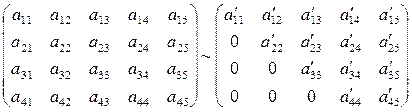здесь столбец 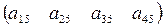— столбец свободных членов системы.

В этом состоит прямой ход метода Гаусса. После его выполнения для отыскания неизвестных осуществляется обратный ход. Последняя строка преобразованной матрицы соответствует уравнению:

.

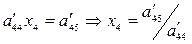Предыдущее уравнение имеет вид:

.

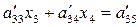Подставляя найденное значение x₄ в последнее уравнение, находим из него x₃. Следующее уравнение 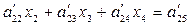уже содержит только одну неизвестную x₂ и последнее уравнение 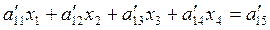только неизвестную x₁. Таким образом, совершая «обратный ход» метода Гаусса находятся все неизвестные системы уравнений.

g Решить систему линейных уравнений:

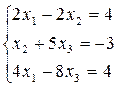
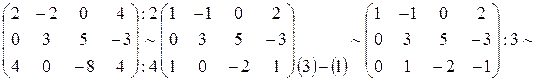
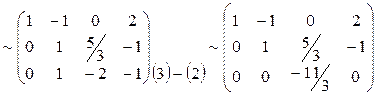
Прямой ход метода Гаусса завершен. Выполните обратный ход.

Однородная система

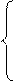
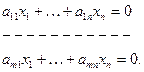
A =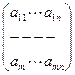

Пусть r (A) = k.

Тогда k уравнений системы являются самостоятельными, остальные уравнения являются следствием остальных.

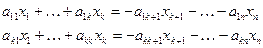
так как r (A) = k. , то определитель

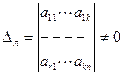
Принимая правую часть системы за свободные члены, решим систему методом Крамера или методом Гаусса. Переменные 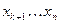могут принимать произвольные значения, а переменные 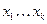будут выражаться через 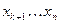. Система имеет бесчисленное множество решений.

Если же дана неоднородная система

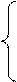
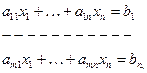
где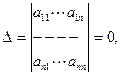

то система имеет бесчисленное множество решений и эти решения находятся таким же способом , что и у однородной системы.

Задание: Решить систему

1.

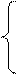
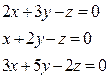
2.

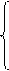
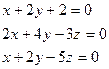
Комплексные числа