Молекулярная физика и термодинамика

2.1. ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ

Молекулярная физика

Количество вещества (молей) однородного газа находится так:

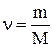, или ,

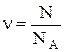где N – число молекул газа; N_A – постоянная Авогадро; m – масса газа; М – молярная масса газа.

Если система представляет собой смесь нескольких газов, то количество вещества системы равно

,

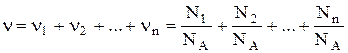или

,

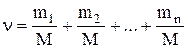где n_n, N_n, m_n, M_n – соответственно количество вещества, число молекул, масса, молярная масса n-го компонента смеси.

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):

,

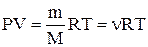где m – масса газа; М – молярная масса газа; R – молярная газовая постоянная; n – количество вещества; Т – термодинамическая температура.

Законы, описывающие состояние газов на основании опытов и являющиеся частными случаями уравнения Менделеева-Клапейрона, для изопроцессов таковы:

а) закон Бойля-Мариотта (изотермический процесс: Т=const, m=const): рV=const, или для двух состояний газа p₁V₁=p₂V₂;

б) закон Гей-Люссака (изобарный процесс: p=const, m=const): 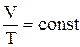, или для двух состояний ;

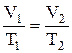в) закон Шарля (изохорный процесс: V=const, m=const): 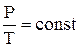, или для двух состояний ;

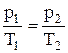г) объединенный газовый закон (m=const): 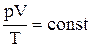, или 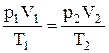, где р₁, V₁, Т₁ – соответственно давление, объем и температура газа в начальном состоянии; р₂, V₂, Т₂ – те же величины в конечном состоянии.

Закон Дальтона определяет давление смеси газов: р=р₁+р₂+…+р_n, где р_n – парциальные давления компонентов смеси; n – число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он находился в сосуде, занятом смесью.

Молярная масса смеси газов:

,

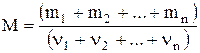где m_n – масса n-го компонента смеси; 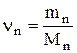– количество вещества n-го компонента смеси; n – число компонентов смеси.

Массовая доля w_n n-го компонента смеси газа в долях единицы или процентах находится так:

,

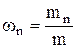где m – масса смеси.

Концентрация молекул:

,

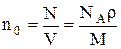где N – число молекул, содержащихся в данной системе; r – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов:

,

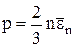где 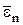– средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы:

,

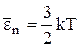где k – постоянная Больцмана.

Средняя полная кинетическая энергия молекулы:

,

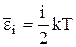где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры такова:

p=nkT.

Скорость молекул:

среднеквадратичная ;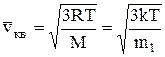

среднеарифметическая ;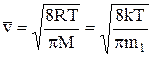

наиболее вероятная ,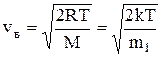

где m₁ – масса одной молекулы.

Относительная скорость молекулы:

,

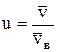где 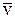– скорость данной молекулы.

Среднее число соударений, испытываемых одной молекулой газа в единицу времени, –

,

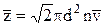где d – эффективный диаметр молекулы; n – концентрация молекул; 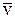– среднеарифметическая скорость молекул.

Средняя длина свободного пробега молекул газа –

.

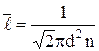Удельные теплоемкости газа при постоянном объеме (с_v) и постоянном давлении (с_р):

.

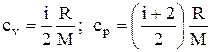Связь между значениями удельной с и молярной С теплоемкости:

.

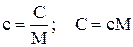Уравнение Майера:

С_р-С_v=R.

Внутренняя энергия идеального газа:

.
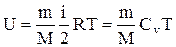