Побудова загального розв’язку лінійного однорідного диференціального рівняння
Лінійні диференціальні рівняння з сталими коефіцієнтами
Розглянемо лінійне диференціальне рівняння 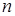 -го порядку зі сталими коефіцієнтами
-го порядку зі сталими коефіцієнтами
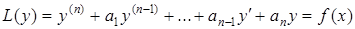 , (5.26)
, (5.26)
де 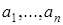 – постійні дійсні числа,
– постійні дійсні числа, 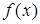 – неперервна функція на
– неперервна функція на 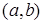 .
.
Разом з неоднорідним диференціальним рівнянням (5.26) будемо розглядати однорідне диференціальне рівняння
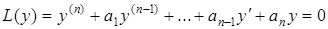 . (5.27)
. (5.27)
Для побудови загального розв’язку диференціального рівняння (5.27) необхідно знайти хоч одну фундаментальну систему розв’язків. Виявляється, що фундаментальну систему розв’язків диференціального рівняння (5.27) можна побудувати з елементарних функцій.
Наприклад, при 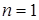 для диференціального рівняння
для диференціального рівняння 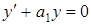 , де
, де 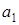 – дійсне число, частинним розв’язком буде функція
– дійсне число, частинним розв’язком буде функція 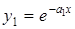 .
.
Дотримуючись ідеї Ейлера, частинні розв’язки диференціального рівняння (5.27) шукаємо у вигляді
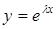 , (5.28)
, (5.28)
де 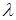 – деякі поки невідомі постійні числа (дійсні або комплексні). Підставимо (5.28) в (5.27) отримаємо
– деякі поки невідомі постійні числа (дійсні або комплексні). Підставимо (5.28) в (5.27) отримаємо
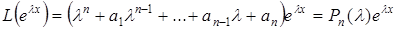 . (5.29)
. (5.29)
З (5.29) випливає, що 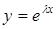 є розв'язком диференціального рівняння (5.27) тоді і тільки тоді, коли
є розв'язком диференціального рівняння (5.27) тоді і тільки тоді, коли 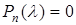 , тобто
, тобто
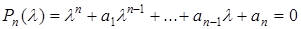 . (5.30)
. (5.30)
Рівняння (5.30) називають характеристичним рівнянням, а його корені характеристичними числами диференціального рівняння (5.27).
Розглянемо три випадки побудови лінійно незалежних розв'язків.
а). Корені характеристичного рівняння 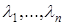 дійсні і різні.
дійсні і різні.
Тоді 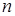 дійсних частинних розв'язків знайдемо згідно формул
дійсних частинних розв'язків знайдемо згідно формул
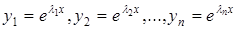 .
.
Ці розв'язки є лінійно незалежними. Дійсно
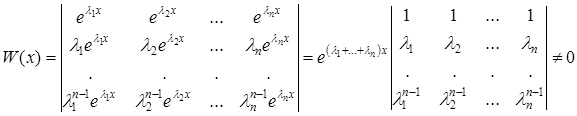 ,
,
так як останній визначник є визначник Вандермонда, який не дорівнює нулю, коли всі числа 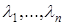 – різні.
– різні.
В цьому випадку загальний розв'язок має вигляд
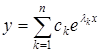 (5.31)
(5.31)
в області
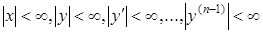 , (5.32)
, (5.32)
де 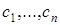 – довільні сталі.
– довільні сталі.
б). Корені характеристичного рівняння всі різні, але серед них є комплексні.
Нехай 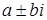 – пара комплексно спряжених коренів. Два дійсних, лінійно незалежних розв’язків будуються таким чином. Кореню
– пара комплексно спряжених коренів. Два дійсних, лінійно незалежних розв’язків будуються таким чином. Кореню 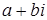 відповідає комплексний розв’язок
відповідає комплексний розв’язок 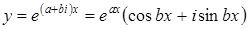 . Згідно доведеному вище, функції
. Згідно доведеному вище, функції 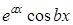 ,
, 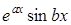 також є розв’язками диференціального рівняння (5.27), які є незалежними в інтервалі
також є розв’язками диференціального рівняння (5.27), які є незалежними в інтервалі 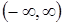 . Аналогічно кореню
. Аналогічно кореню 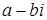 відповідають два дійсних, лінійно незалежних розв’язки
відповідають два дійсних, лінійно незалежних розв’язки 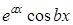 ,
, 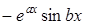 . Їх приєднання до знайдених дають лінійно залежну систему розв’язків. Тобто, спряжений корінь не приносить нових дійсних лінійно незалежних частинних розв’язків.
. Їх приєднання до знайдених дають лінійно залежну систему розв’язків. Тобто, спряжений корінь не приносить нових дійсних лінійно незалежних частинних розв’язків.
Таким чином, кожній парі комплексно спряжених коренів відповідає два дійсних лінійно незалежних розв’язки виду
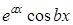 ,
, 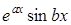 ,
,
які разом з розв’язком 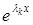 (
( 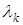 – дійсні числа) утворюють фундаментальну систему розв’язків на інтервалі
– дійсні числа) утворюють фундаментальну систему розв’язків на інтервалі 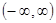 .
.
Приклад 5.6. Знайти загальний розв’язок диференціального рівняння
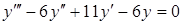
Розв'язання. Запишемо характеристичне рівняння і знайдемо його розв'язки
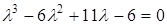 ,
, 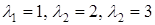 .
.
Тоді
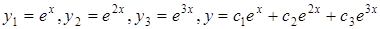
– загальний розв’язок.
Приклад 5.7. Знайти загальний розв’язок диференціального рівняння
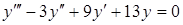 .
.
Розв'язання. 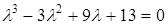 ,
, 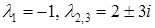 ,
,
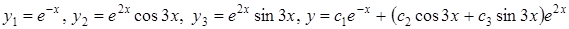 –
–
загальний розв'язок.
Приклад 5.8. Знайти загальний розв’язок диференціального рівняння
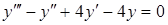 .
.
Розв'язання. 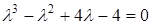 ,
, 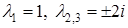 ,
,
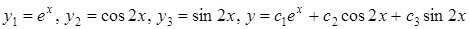 .
.
в). Випадок наявності кратних коренів характеристичного рівняння.
Припустимо, що 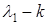 -кратний корінь характеристичного рівняння (5.30), так що
-кратний корінь характеристичного рівняння (5.30), так що
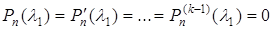 , але
, але 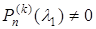 . (5.33)
. (5.33)
Щоб знайти розв’язки, які відповідають характеристичному числу 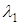 , продиференціюємо тотожність
, продиференціюємо тотожність
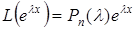 (5.34)
(5.34)
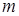 раз по
раз по 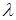 , використовуючи при цьому формулу
, використовуючи при цьому формулу
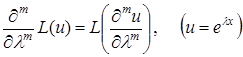 .
.
Для знаходження похідної від добутку функцій використовуємо формулу Лейбніца
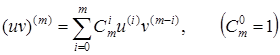 ,
,
де
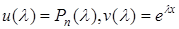 .
.
Маємо
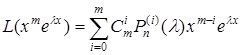 .
.
Використовуючи (5.33), запишемо
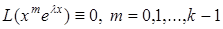 ,
,
тобто функції
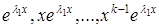 (5.35)
(5.35)
є розв’язками диференціального рівняння (5.27). Ці функції лінійно незалежні на 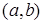 .
.
Таким чином, кожному дійсному кореню 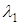 кратності
кратності 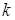 відповідає
відповідає 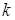 дійсних лінійно незалежних розв’язків виду (5.35).
дійсних лінійно незалежних розв’язків виду (5.35).
Якщо характеристичне рівняння має комплексні корені 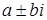 кратності
кратності 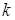 , то
, то 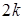 лінійно незалежних розв’язків будуть мати вигляд
лінійно незалежних розв’язків будуть мати вигляд
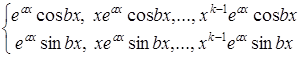 . (5.36)
. (5.36)
Розв’язки (5.36) лінійно незалежні на інтервалі 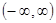
Приклад 5.9. Розв’язати диференціальне рівняння
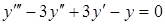 .
.
Розв'язання. Запишемо розв’язки характеристичного рівняння
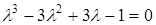 ,
, 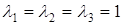 .
.
Тоді
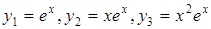 ,
, 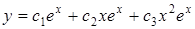
– загальний розв’язок.
Приклад 5.10. Розв’язати диференціальне рівняння
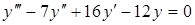 .
.
Розв'язання. 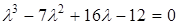 ,
, 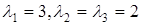 ,
,
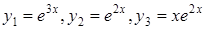 ,
, 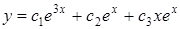
– загальний розв'язок.
Приклад 5.11. Розв’язати диференціальне рівняння
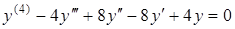 .
.
Розв'язання. 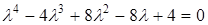 ,
, 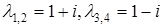 ,
,
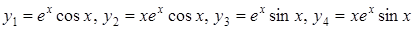 ,
,
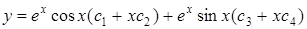 – загальний розв'язок.
– загальний розв'язок.
