Передача дискретных сообщений по каналам связи

Канал связи представляет собой совокупность технических средств и физических сред, предназначенную для передачи сообщений из одной точки пространства в другую. Эта передача чаще всего осуществляется в условиях неизбежных помех. В результате воздействия помех каждый отправленный символ x_iможет быть опознан получателем как символ 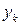, причем y_k 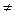x_i. Такое событие называют ошибкой.

Передачу символов сообщения можно рассматривать как составной эксперимент, состоящий в отправлении символов сообщения 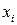и получения символов 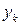. С точки зрения теории информации физическое устройство канала несущественно, а свойства канала при этом полностью описываются матрицей переходных вероятносте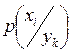й или ,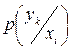

где 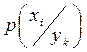есть вероятность передачи символа 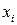, если зафиксирован полученный символ ,

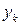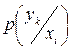– вероятность получения символа 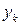, если зафиксирован (передается) символ .

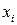При этом предполагается, что новые символы (сверх заданного объема алфавита m) не могут быть созданы под влиянием помех.

Следовательно,

; .

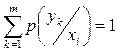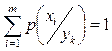Если помехи отсутствуют, то все диагональные элементы матрицы 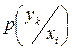или матрицы 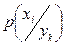равны единице, а остальные – нулю. При очень больших помехах все элементы матриц могут быть приблизительно одинаковыми.

При наличии помех, передача символа 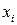не снимает полностью неопределенность относительно полученного символа 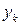. Таким образом, передача символов по каналу описывается ниже перечисленными мерами неопределенности (энтропиями).

Неопределенность передаваемых символов при условии их независимости :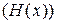

.

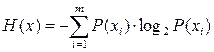Неопределенность полученных символов :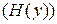

.

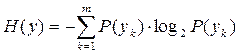Неопределенность получения символов при зафиксированном символе :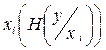

.

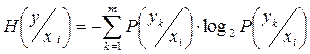Эта величина называется частной энтропией принятых символов.

Полная энтропия принятых символов вычисляется усреднением 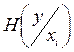по вероятностям передаваемых символов :

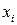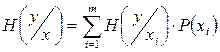Величину 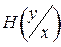называют средней условной энтропией принимаемых символов.

Неопределенность передаваемых символов при зафиксированном принятом символе :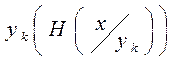

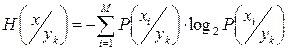Эта величина является частной энтропией передаваемых символов.

Полную энтропию передаваемых символов находят усреднением энтропии 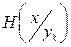по вероятностям принимаемых символов :

.

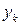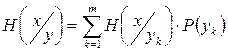В соответствии с основным соотношением теории информации (1.3), прирост количества информации (I ), связанный с приемом одного символа сообщения, определяется выражением:

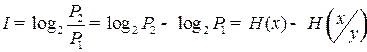(3.1)

где 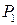– априорная вероятность появления символа;

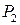– апостериорная вероятность появления этого же символа. Справедливо также соотношение:

.

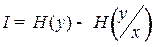(3.2)

Из выражений (3.1) и (3.2) видно, что, по мере уменьшения помех, величина 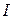будет стремиться к 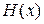, а при увеличении помех будет стремиться к нулю.